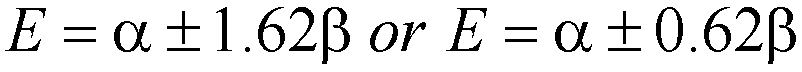The Hückel p molecular orbitals of 1,3-butadiene

· Solving the secular determinant gives the molecular orbital energies.

· It also ensures that at these energies the secular equations will have a nontrivial solution (i.e. a solution other than all the coefficients in eq. 1 being 0).

We now expand the secular determinant:

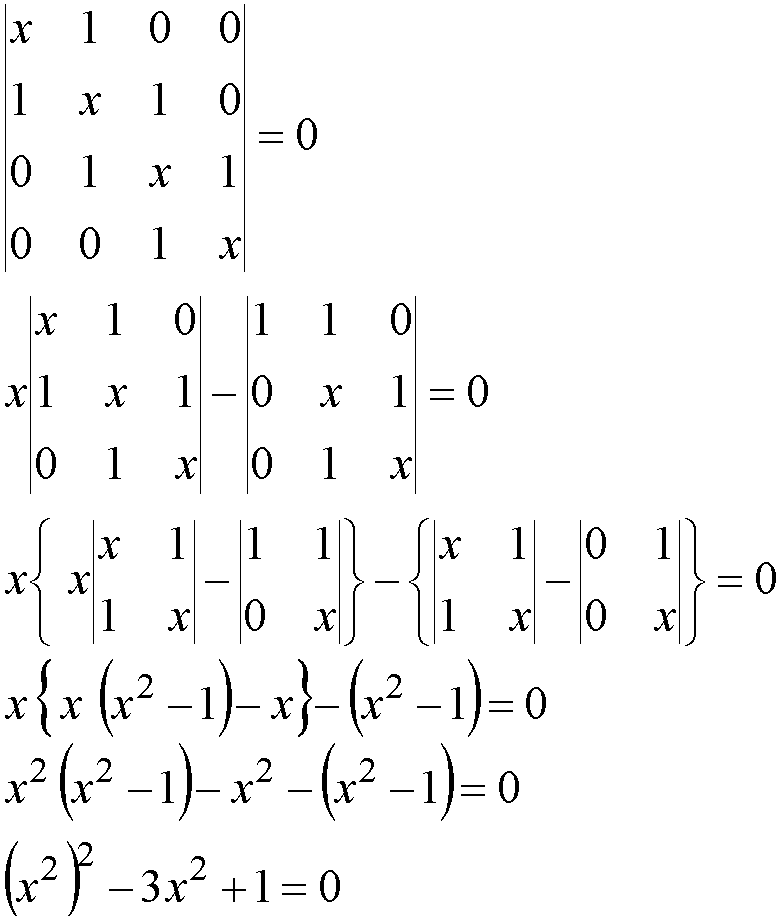
Let y = x², then:

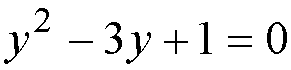
This is a quadratic equation. The solution is:

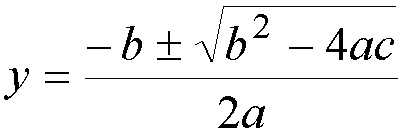
a = 1, b=–3, c=1.

Therefore:

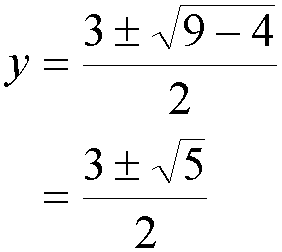
y = 2.62 or 0.38

i.e.

x² = 2.62 or 0.38

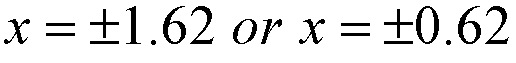
There are 4 solutions (remember ).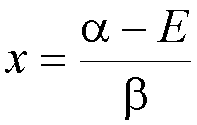

The 4 molecular orbital energies are:

The molecular orbital diagram for 1,3-butadiene