A2. Operation of the Quadrupole Mass Spectrometer

 

A large part of this PhD work has been involved with optimising a state of the art Quadrupole Mass Spectrometer (HIDEN, HAS-5PL-4353).  This Mass Spectrometer has been developed for plasma analysis sources and is conveniently called an Electrostatic Quadrupole Plasma Probe or EQP.  The EQP can be used in two operating modes, the Residual Gas Analysis (RGA) mode to record spectra of neutral species in the plasma and the Secondary Ions Mass Spectrometry (SIMS) mode to record spectra of ionised species in the plasma.  As stated in Chapter 2 the mass spectrometer can be divided into five regions, which will be discussed in technical detail.

 

A2.1. Detailed Description of the Apparatus

 

A detailed figure of the Mass Spectrometer with its associated electrostatic lenses is given in Figure 2.1.  The entrance pinhole has a chosen diameter of 2 mm.  This diameter of pinhole was necessary in order to obtain a good signal to noise for the spectra because the plume is typically sampled at ~275 mm from the target. 

Highly important for understanding the operation of the EQP is a detailed knowledge of its electrical circuitry.  The lenses are set at defined potentials by several independent power supplies.  These independent power supplies are connected to each other as illustrated in Figure 2.2.  An understanding of the operation of each power supply and the effect of a set voltage on the connected electrodes is essential for understanding the operation of the EQP.

 

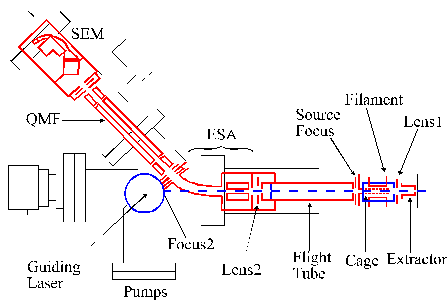
Figure 2.1: Detailed figure of the Mass Spectrometer with its associated electrostatic lenses (ESA = Electrostatic Analyser, QMF = Quadrupole Mass Filter, SEM = Secondary Electron Multiplier).  The components in blue are adjusted to our specific needs.

 

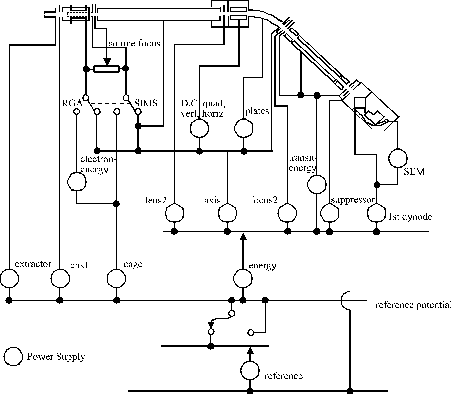
Figure 2.2: Circuit diagram showing the various bias voltages and their connections within the Hiden mass spectrometer.

For example, scanning energy scans not only the voltage on axis but also on lens2, focus2, transit-energy, suppressor and 1^st dynode.  When changing any voltage care must be taken to assess which other voltages will change and the effect they will have.

The reference power supply allows detection of particles with energy ≤ 1100 eV.  For example, by setting this voltage at 200 V, every other electrode is also set at 200 V plus their respective individual power supply voltage.  Energy can only scan between ‑100 and +100 eV.  In order to scan an energy range of 0-300 eV, two separate scans will be needed.  Longer scans in energy space are possible by scanning reference but, in doing so, extractor and lens1 are also scanned, which is unfavourable. 

Many of the voltages displayed in Figure 2.2 are determined by the manufacturer and seldom need to be changed.  The machine specific values for these voltages are determined when the instrument was initially tuned.  The voltages on all of the electrodes are crucial if the apparatus is to be operated correctly, and it is important to discuss the specifics of these lenses.  The apparatus can be divided into five separate regions, as previously discussed:

 

The extraction region

 

The extraction region exists of two electrostatic lenses, the extractor and lens 1.  The extraction region is very important when measuring ion currents in SIMS mode.  A more detailed discussion of the influence of these two lenses on the transmission of the ions through the EQP is given later in this Appendix.  When recording ion spectra the voltage on these lenses was set to 0 V (or –reference, see earlier discussion) since the ions in this study are clearly travelling with non thermal velocities (e.g., for the ablation of graphite, at up to 200 eV).  The extraction region is of lesser importance for the detection of neutral particles (RGA mode) in the ablation plume, since they are not affected by the voltages on these lenses.  In RGA mode, the extraction region can be used to repel accompanying ions in the plume.

 

The source region

 

The source region is important when recording spectra in RGA mode, since this is the region where ions are created from neutrals via electron bombardment.  The electron source comprises two tungsten filaments which can be both switched on at the same time.  The electrons are accelerated in the cage for ionisation.  In standard mode both of the filaments are set to an emission current of 1000 mA and the electron acceleration voltage is set to 30 V.  The cage can be set on a positive voltage to accelerate thermal species without flow velocity, into the mass spectrometer.  In the present work, however, this voltage has been set to 0 V since the ablation plume is expected to exhibit a centre of mass velocity distribution.  The neutral distribution has been proposed to have a 2-3 times smaller mean velocity than the ions in a standard ablation experiment,^[1] thus the mean centre of mass kinetic energy of the neutral species in our ablation plume is not expected to be higher than 10 eV.  The ionised neutral species are subsequently focused at the beginning of the field free region.  The optimal value for the voltage on the source focus in our experiments was found to be -67 V.  From the connection diagram (Figure 2.2) it is obvious that in SIMS mode the source region is set on the same potential as the field free region and simply acts as an extension to the field free region. 

 

The electrostatic analysis region

 

The electrostatic analysis region exists of a field free region with a quadrupole energy filter positioned behind it.  Kinetic energy selection is obtained since the ions transit through the field free region with an energy which is equal to the sum of the axis voltage and the energy voltage.  Since the axis voltage is typically –20 V, the particles with an initial energy equal to the energy potential will have a kinetic energy of 20 eV after the field free region.  The Electrostatic Analyser (ESA) is tuned so as to transmit only particles with a kinetic energy towards the detection region equal to the axis potential.  Lens2 focuses the ions into the ESA for energy filtering (the voltage is typically set to 20 V).  The ESA is a 45° sector field energy analyser which is controlled by plates, vert, horiz, D.C. quad and axis.  The D.C. quad region is tuned up via an iterative procedure to optimise the signal.

The advantage of locating the ESA before the quadrupole mass filter, as compared with other experimental QMS or TOF set-ups, is that it is then not necessary to make any assumptions about the residence time within the mass filter, which can critically influence such measurements.^[2]  The residence time in a normal QMS set-up has to be known since the energy of the particles are measured via their TOF profile after mass selection.  With thermal species (< kT) this residence time can be assumed constant, but for high kinetic energy particles the residence time becomes a complicated function of both its mass and energy.

 

The quadrupole mass filter

 

After kinetic energy selection by the ESA, the ions are decelerated and focused by focus2 before injection into the quadrupole mass filter (QMF).  The QMF consists of a main filter driven by RF and DC, with a pre- and post-filter driven by RF only.  Transit_energy is a virtual voltage source which allows the energy for the ion transit through the QMF to be explicitly set (typical voltage: 3V).

 

The detection region

 

The detector is an ion counting secondary electron multiplier (SEM) which is mounted off-axis.  1^stDynode sets the voltage on the front of the detector.

 

During our work with the mass spectrometer a number of modifications have been introduced in an attempt to meet the specific needs imposed by studying a plasma generated by laser ablation (shown in blue in Figure 2.1).  One important adjustment was the introduction of a small diode laser to enable precise alignment of the mass spectrometer axis to the ablation spot.  Also, additional pinholes have been introduced in an effort to ensure transmission of only those particles that are almost solely forward directed, i.e. with minimal off-axis velocity component.  The source region was also rebuilt to enhance the ionisation cross-section.  This was necessary because of the low density of the ablation plume at the detection distance.

 

A2.2. Specific usage of the EQP in Laser Ablation

 

Since pulsed laser ablation is a time gated event, the EQP has to be used in time gated mode also.  The triggering and time gate arrangement normally used is illustrated in Figure 2.3.  This set-up also ensures a high signal to noise ratio.  The acquisition time for a single point on an energy scan ranged between 5-25 ms which, given the 0.5 ms time gate used, means that every point on an energy spectrum is an accumulation of 10-50 shots.  This set-up obviously leads to very long acquisition times (for example recording 400 points at 25 ms acquisition times equates to > 30 minutes ablation time) and, as discussed in Chapter 2 such time scales are too long to perform in a single ablation run.  The solution to this problem is to record a complete spectrum in several separate ablation runs, or to record a spectrum with a smaller number (~ 50) of points.

 

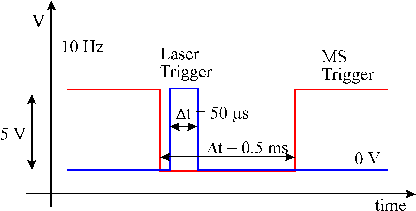
Figure 2.3: Time gating of the mass spectrometer

 

The (x,y) translation stage is used to provide a fresh target surface when recording the spectra.  This method worked well in most circumstances although some considerations when operating with the (x,y) translation stage have to be taken into account. Firstly, the area through which the target can be rotated is fully exposed in ~30 minutes, precluding experiments that extend beyond this period.  Second, the ablation yield can be very sensitive to the surface morphology, so high surface uniformity is desirable.  To this end, it is best to work with a mirror polished target sample, and to gently pre-ablate the entire surface area of interest prior to the mass spectrometer investigation.  There are situations where the earlier rotating target design is preferable, e.g. when performing near-threshold ablation studies (where signal levels are necessarily small), since the (x,y) translation stage introduces a higher degree of contamination into the vacuum.

To counter this latter problem a purpose built cold finger can be attached to the laser ablation chamber when performing low fluence studies.  This consists of a copper rod inserted in the vacuum and in contact with liquid nitrogen through a stainless steel mantle.  The design is shown in Figure 2.4.  The contamination of the vacuum is reduced by applying this cold finger, resulting in a ~10´ reduction in the base pressure of the vacuum chamber.

 

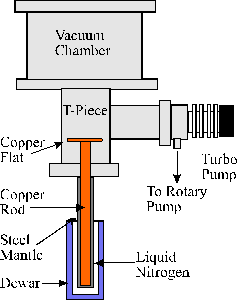
Figure 2.4: Cold finger design.

 

A2.3. Experimental Determination of the System Performance

 

The experimental determination of the system performance has to deal with two questions.  First of all, does the apparatus provide a well-calibrated energy scale?  If this requirement is met the second question is whether the energy dependent transmission function is a smooth curve, ideally a straight line with gradient of 0.  As shown in Chapters 3-5 this is a critical requirement, especially in laser ablation applications since the ion kinetic energy can have a very broad distribution stretching from 0 eV till hundreds of eV.  This behaviour is quite unique to ablation generated plasmas in vacuum and will impose some severe demands on the detection apparatus.  The neutral fragment distribution is expected to be much narrower and to have a lower mean kinetic energy (< 10 eV).  The different restrictions for the two operational modes, RGA and SIMS mode, are discussed in the following paragraphs.

 

A2.3.1. RGA mode

 

The validity of the energy scale and the energy dependence of the transmission function in RGA mode can be assessed experimentally by applying a voltage to the cage electrode while monitoring the energy distribution of a residual gas in high vacuum (in our case N₂ in 5 ´ 10^-8 Torr).  Sample results are shown in Figure 2.5.  The maximum cage voltage is 10 V so the apparatus can only be calibrated for particle kinetic energies ≤ 10 V, which is probably sufficient for the present application.

 

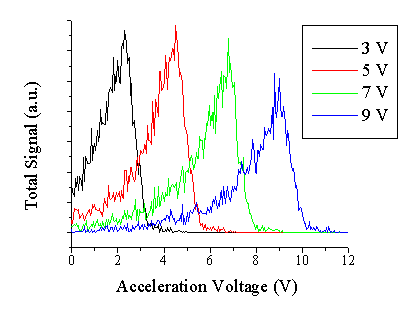
Figure 2.5: Determination of the energy scale and the transmission function in RGA mode, the cage voltage has been varied from 3 to 10 V so as to accelerate the ions generated within the source region towards the TOF tube. Assuming a thermal velocity for these generated ions, the voltage on the cage will accelerate them to a terminal velocity of a maximal value (in eV) of cage voltage.

 

Not only the energy scale is in good accordance with the expected values, but also the transmission function appears to be relatively independent of the kinetic energy.  This analysis suggests that the monitoring of the neutral particles and their kinetic energy distribution in the ablation plasma is valid within the 0-10 eV region.

A2.3.2. SIMS mode

 

A calibrated ion source producing high kinetic energy ions is necessary for the calibration of the ion energy scale in SIMS mode.  A suitable Cs⁺ ion source was provided by HIDEN.  It consists of an ion generation region comprising a piece of Cs containing glass (Kimball) heated by two filaments.  The ions are initially accelerated in a focusing optic (Bessel box) and are further accelerated to yield ion kinetic energies in the range of 30-100 eV.  The energy calibration in SIMS mode, shown in Figure 2.6, reveals an excellent agreement between the ion energies calculated from the known accelerating potentials and those recorded by the mass spectrometer.

 

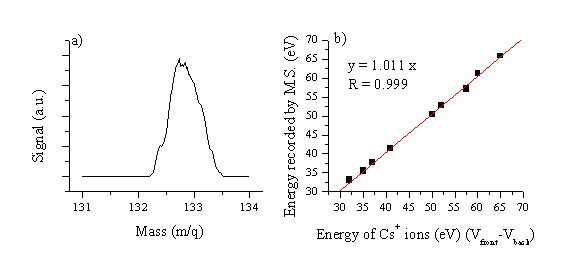
Figure 2.6: (a) Recorded mass spectrum of Cs⁺ ions, and (b) energy calibration in SIMS mode.

 

Unfortunately, the transmission function cannot be deconvoluted from this experiment.  A comparison between the kinetic energy distributions of C⁺ ions resulting from graphite ablation in vacuum measured using the Faraday Cup and with the Mass spectrometer is shown in Figure 2.7. Clearly, these reveal huge differences.  The transmission function thus appears to be highly dependent on the kinetic energy of the particles. 

 

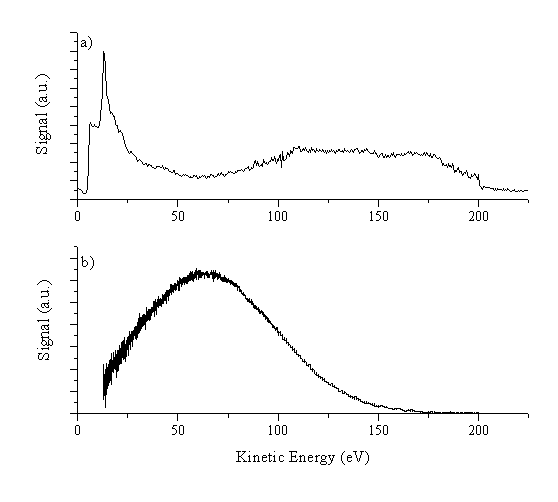
Figure 2.7: Comparison of the kinetic energy distributions of C⁺ ions from 193 nm ablation of graphite in vacuum as recorded by (a) mass spectrometer and (b) Faraday Cup for a fluence of 2.5 J/cm².

 

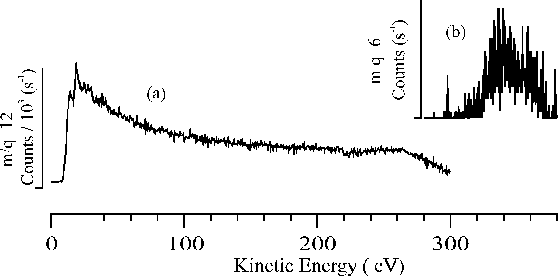
The first attempt to overcome the problem of deconvoluting the transmission function was a purely experimental approach, involving tuning of voltages on the extractor and lens 1 ion optics so as to ensure maximum transmission for every energy.  For this approach the kinetic energy spectrum was taken in chunks ranging from a few eV to a few tens of eV and the settings for the voltages on the lens 1 and extractor electrodes were optimised for every kinetic energy region.  The resulting spectra for C⁺ and C²⁺ ions are shown in Figure 2.8.

 

Figure 2.8: Mass spectrometer measurements of the ionic components in the ablation plume following 193 nm irradiation of graphite at a fluence of 20 J/cm².  The C⁺ signal was monitored at m/q = 12 and the C²⁺ was monitored at m/q = 6.  The extractor lens and lens 1 were tuned up for different energy regions to obtain maximal transmission for the whole energy range.

 

Clearly this procedure yields a much smoother kinetic energy distribution, but it is still not in accord with the Faraday Cup spectra.  The main reason for this is the incorrect assumption that the mass spectrometer, even if tuned up, will necessarily have the same transmission for particles with different kinetic energies.  A more detailed discussion about the reasons underlying the inherent kinetic energy dependent transmission function of the apparatus is given below.

 

A2.4. Modelling of the Transmission Function with SIMION

 

The transmission of ions through the mass spectrometer has only been modelled for the SIMS mode of operation since the transmission of these particles through the mass spectrometer seem to show the greatest kinetic energy dependence.  As discussed in section A2.1, all the ions transmitted through the ESA and into the QMS will have the same kinetic energy (axis potential).  Thus the transmission function beyond the field free region should only be mass and not kinetic energy dependent.  Thus only the front region of the mass spectrometer, up till the ESA in Figure 2.1, needs to be considered when investigating the kinetic energy dependent transmission function for a given ion mass/charge ratio.  A model of the front part of the mass spectrometer has been provided by Hiden in the form of a SIMION potential array file and the SIMION software ^[3] has been used to study the trajectories of ions in these electric fields and thus the energy dependent transmission.  For the calculations we have concentrated on the transmission function of singly charged carbon cations (m/q = 12).

The first study we have performed is to model and compare the energy dependent transmission behaviour of the mass spectrometer when ions enter with either only a forward velocity component or with both forward and radial velocity components, a small angle of ± 4° was chosen.  For these calculations the voltages on the lens1 and extractor ion optics were set to 0 V, and the potential on the ionisation region and axis was set to (–20 V + Energy (see Figure 2.2)), to resemble closely the standard experimental conditions.  The results, shown in Figure 2.9, reveal that in both of the cases the transmission function is far from an ideal smooth horizontal line.  The experimental curve shown in Figure 2.8 bears more resemblance to the case where the ion beam has a radial velocity component.  This is consistent with the experimental observations reported in Chapters 4 and 6.  In the further discussion only calculations with a ± 4° angular spread will be considered.

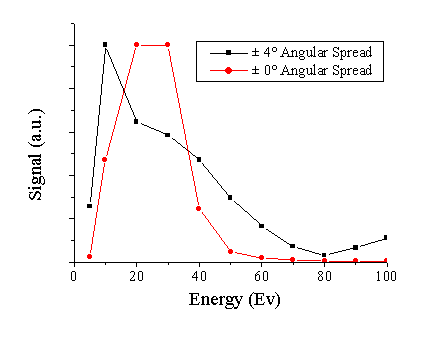
Figure 2.9: Calculated transmission function for (red) 0° and (black) ±4° angular spread of the incoming ions, for energies of 0-100 eV.

These transmission functions have been obtained by calculating the trajectory of 50,000 individual ions for every calculated kinetic energy with a spread of initial directions (given by an angular value defined relative to the instrument axis), and by changing the radius of the ion incidence relative to the centre of the mass spectrometer by a given distance.  The transmission efficiency for every radius has to be multiplied by the circumference of the circle, since we are modelling a 2-D slice from a 3-D situation.  These calculations are quite time demanding and inefficient.  For these reasons, a Monte Carlo add-in program was implemented in the SIMION software that allowed randomised selection of the initial angle and radius of the incident ion.  With this Monte Carlo routine, we could reduce the number of ions per run drastically, normally 1000 ions per run was used to produce qualitatively the same result as the non-Monte Carlo result.

The reason for the dramatic energy dependence of the transmission function was identified as, primarily the region between lens 1 and the source region (maintained at axis + energy potential, see section A2.1).  Indeed, when the electric field gradient is plotted out in the SIMION image a kinetic energy dependent electric field is observable between lens 1 and the source region, which acts as a lens (see Figure 2.10).  This lens has a energy dependent focusing effect as can be observed from the trajectories of ions of different kinetic energies.  The focal point for different kinetic energies can be deduced from the calculations and figures for different kinetic energy ions are given in Table 2.1 (also consider Figure 2.10 for comparison of the focal lengths).

 

Table 2.1: The distance of the focal point, calculated from the extractor entrance for different kinetic energies.  Only particles with angular spread of ± 0° were used in the trajectory calculations.  The figures can be compared with the red curve in Figure 2.8.

The figures in Table 2.1, show that the focal point of this kinetic energy dependent lens is highly affected by the kinetic energy of particles (or the Axis-Energy potential).  This lensing effect is depicted as the main reason for the large kinetic energy dependency of the transmission function.

 

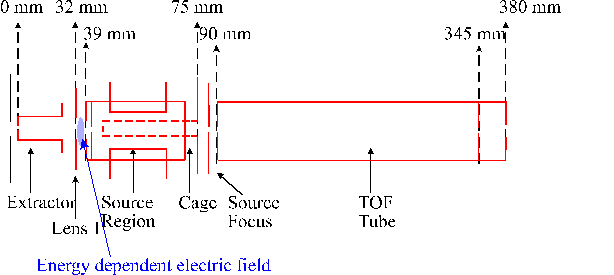
Figure 2.10: Detailed image of the energy selection region of the mass spectrometer (before the ESA), with dimensions.  The region in light blue shows the energy dependent electric field.

 

A second point we have to address is the accuracy of the SIMION calculations and the agreement between such simulations and experiment. Figure 2.11 compares calculations for two different settings of the axis potential (20 and 40 V) with experimental spectra recorded with the mass spectrometer under the same conditions. It is important to recognise that the experimental data is a convolution of the carbon ion kinetic energy distribution and the transmission function, so the curves can not be directly compared with each other.  Nevertheless, the calculated curves show qualitative accord with the experimental data, in agreement with the notion that the experimental curve is in fact a much smoother energy dependent function (as implied by the Faraday Cup measurements).

 

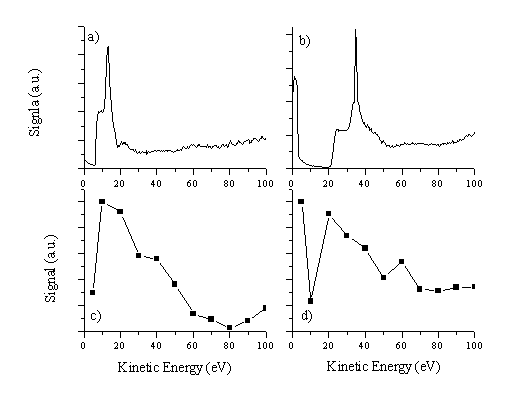
Figure 2.11: Experimental spectra (a) and (b) taken with the mass spectrometer in SIMS mode for carbon ions (m/q = 12) with the standard voltages on the lenses (0 V on extractor and lens 1) and, (a) 20 V and (b) 40 V for the axis voltage and a ± 4° angular spread.  Theoretical spectra obtained from SIMION calculations for the same voltage settings on the lenses and with a voltage of (a) 20 V and (b) 40 V on the axis.

 

Unfortunately, the calculated curves can not be used for any quantitative assessment of the kinetic energy dependent transmission function.  The main reason for this is that the SIMION calculations consider a set of non-interacting ions, which is a poor representation of the reality.  The optics focus the ions to a focal point the position of which is kinetic energy dependent (see Table 2.1).  It is highly unlikely that particles with the same kinetic energy will not interact in these focii (where the mean distance between the particles is the smallest).  SIMION has an option of including allowance for repulsion between ions but a correct value for the interaction can not be given since this value is dependent on the ion density -which is the property we are trying to deconvolute!  Thus this is an ill-defined problem.  The SIMION results, even neglecting inter-ion repulsion, can nevertheless still be validated as predictor values to gain insight into the behaviour of the mass spectrometer.

A2.5. Experimentally Determined Transmission Function

 

If we assume that the Faraday Cup signal is the true kinetic energy dependent ion distribution then we can deconvolute the mass spectrometer transmission function.  The resulting deconvolution gives a transmission function in terms of a 9^th order polynomial with the expression:

 

y = A + B₁ E + B₂ E² + B₃ E³ + ¼ + B₉ E⁹

 

where E stands for the energy (in eV).  Representative figures for the coefficients are given in Table 2.2.  This set of figures are for the mass spectrometer operating in SIMS mode and for the following voltages on the lenses in the front of the mass spectrometer: 0 V on extractor and lens 1, and -20 V for the axis potential.  Since the transmission function is expressed as a energy dependent function, it is assumed to be mass and charge independent.  This transmission function is fitted in between a kinetic energy window of 0-200 eV, and it does not represent the transmission function at higher kinetic energies.

 

Table 2.2: The values for the different coefficients for the 9^th-order polynomial fit for the following conditions: extractor and lens 1 at 0 V and axis at 20 V.

Additionally, we have also studied the cases of putting a small attracting and repelling voltage (± 5 V) on the ion optic lens 1 next to a large attracting voltage (-50 V) to obtain information about correction for the large differences in the kinetic energy dependent transmission function. The results of the calculations are given in Figure 2.12.  Different voltages on lens 1 yield different transmission functions, which is expected.  None of the transmission functions seem to be smoother than the original transmission function (0 V on lens 1), showing that applying voltages on the ion optic lens 1 will not greatly improve the energy dependence of the transmission of the mass spectrometer.

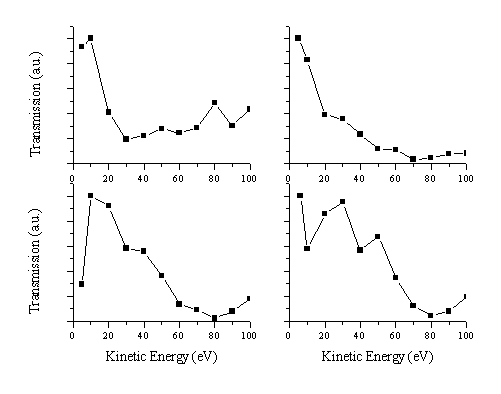
Figure 2.12: Calculated transmission function for different voltages on lens 1, (a) –5 V, (b) –50 V, (c) 0 V and (d) 5 V.

 

A2.6. Conclusion

 

The performance of a state of the art QMS specifically built for analysis of ablation plumes has been investigated.  The conclusion of the performance can be divided in 2 parts. 

1.      For detecting neutral atoms in RGA mode, the mass spectrometer operates adequately.  As derived from experimental data, the transmission function is not dependent on the kinetic energy of the particles (in between 3-10 eV) and the improved source region enables detection of neutral species in low density ablation plumes.

2.      In SIMS mode, for detection of ions, the mass spectrometer exhibits a detrimental in-built flaw.  Because of its construction it has a highly kinetic energy dependent transmission function.  This problem can only be solved by reconstruction of the front end of the mass spectrometer, e.g. by introducing a set of highly transmitting grids in between the ion optics lens 1 and source region.  This will deplete the electric field curvature between those two optics, which will enhance the transmission function.

 

Throughout this thesis it has been shown that the ionic species within the ablation plume are easily detected with a number of other techniques (e.g. OES, Faraday Cup, Langmuir probes), while information about the atomic species is much more difficult to access.  Since the strength of this QMS lies in the detection of neutral species, studying the atomic species within the plume with this system can add to the understanding of the ablation process.

 

A2.7. References