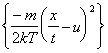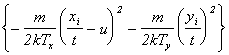4. The UV pulsed laser ablation of graphite and the pulsed laser deposition of Diamond Like Carbon

 

The pulsed laser ablation (PLA) and deposition of graphite have been studied in this work by various techniques.  The ablation event has been studied using an assembly that allows direct investigation of the absorption of the graphite plume by monitoring the amount of laser light transmitted through a small hole (200 mm diameter), mechanically drilled in the target surface, as a function of fluence.  This direct observation of the laser light yields a qualitative understanding of extent to which and the processes by which, laser light is absorbed by the ablation plume.

Further investigations of the laser induced ablation plume have been performed using wavelength, time and spatially resolved OES and by temporal and angular resolved Faraday Cup measurements of the positively charged ions.  The optical emission studies give information about the excited and radiatively decaying species within the plume while the Faraday Cup measurements provide information about the total ion distribution.  Comparison of these results has led to the formulation of a simplified 2-dimensional model of the ablation event to explain the apparent contradictions between the optical emission and the Faraday Cup results. 

In addition, the pulsed laser deposition of Diamond Like Carbon (DLC) has been studied from ablation of two different targets, namely graphite and CVD diamond.  The sp³ fractions of the deposited films were derived from Raman spectrometry, and their Field Emission were studied.  Finally, as a small addition to this work, doping of DLC films with sulphur has been attempted, and the deposition process and the produced films have been partially characterised.

 

4.1. Introduction

 

Graphite is an attractive target material for fundamental studies of PLA, both because of its intrinsic elemental simplicity and because of the wide potential applicability of hard hydrogen-free diamond-like carbon (DLC) films.^[1]  It has been the subject of several previous investigations; indeed, graphite was one of the first target materials to be ablated when the pulsed ruby laser first became available.^[2]  Subsequent studies of the PLA of graphite using long excitation wavelengths (e.g. 1064 nm) have shown the ablation plume contains a high proportion of small carbon cluster species (ions and neutrals).^[3]-[4][5]  DLC films in which an estimated 70% of the C atoms show sp³ (tetrahedral) co-ordination have been reported following 1064 nm laser ablation of graphite, in vacuum, but only at laser intensities approaching 10¹⁰ W/cm².^[6]  Such observations should be contrasted with PLA induced using short wavelength ultraviolet (UV) laser radiation (e.g. 193 nm radiation), where the plume is dominated by atomic species (C neutrals and ions),^[7]-[8][9] and high quality DLC films containing >90% sp³  bonded C atoms have been reported using much lower intensities (~5´10⁸ W/cm²). ^{6,[10]-[11][12][13]}  Such observations support the consensus view that high (~100 eV) impact energies encourage formation of dense sp³ (rather than graphitic) networks in the deposited film,^{1,[14]-[15][16][17][18][19]} and that high ejection velocities are a feature of UV laser ablation rather than more thermally driven (VIS-IR) ablation.  Nonetheless, many details of the ablation process including, for example, factors which affect the plume composition and properties, and how these then in turn influence the resulting film characteristics, merit further study. 

 

4.2. Experimental

 

The general experimental set-up has been discussed in detail in Chapter 2.  The experiments performed on the pulsed laser ablation of graphite were: direct measurement of the attenuation of the laser light by the plume, and optical emission and the Faraday Cup measurements of particles within the plume.  The angular dependency of the total ion signal was determined via Faraday Cup measurements in combination with the translation stage target holder.  This target holder can be rotated manually about the vertical axis (z) and locked in any user-selected orientation relative to the laser propagation axis.  The translation stage rasters the target in the yz plane relative to the fixed laser focus, thereby allowing each laser shot to ablate a fresh area of the graphite surface.  The optical emission was recorded using the procedures described in Chapter 2, both OES and CCD camera imaging were employed.

The pulsed laser deposition studies employed standard conditions for DLC film growth, i.e. high vacuum, room temperature substrate.  The films were analysed by Raman spectroscopy and subjected to Field emission testing.

 

4.3. Direct measurement of the attenuation of the laser light by the plume

 

Attenuation of the laser light by the plume was studied directly, by recording the temporal transient of the laser pulse obtained by coupling the laser light onto a fast photodiode after it had propagated through a small, mechanically drilled, hole through the target.  Pictures of a typical hole are as shown in Figure 4.1(a).  The dimensions of the hole were chosen so as to be sufficiently small compared to the laser spot size to cause only a minor perturbation to the amount of ejected particles, but big enough to allow a detectable amount of light through the aperture.  Given a laser pulse footprint on the target of 1 ´ 0.4 mm² and a hole diameter of 200 mm the area of the hole is less than 10% of the total ablated area.  An image of the post-ablated area is given in Figure 4.1(b).

 

Figure 4.1: Selected SEM images of the mechanically drilled holes in the target, (a) top view, the hole diameter is ~ 200 mm (b) side view after ablation, the hole is positioned in the middle of the ablation spot.

 

This set-up is used to investigate the absorption mechanism of the laser light by the ablated plume.  The two main absorption mechanisms in a monoatomic ablation plume are multi-photon ionisation (MPI) and electron-ion inverse Bremsstrahlung (IBE).  Electron-neutral inverse Bremsstrahlung plays a minor role under these experimental conditions.^{[20],[21]  Another mechanism that could cause attenuation is photodissociation of larger clusters emitted by the surface.  To our knowledge, there is no quantitative information about the ejection rate of larger clusters from graphite arising from 193 nm ablation, although the optical emission of the ablation plume (section 4.4) suggests that larger clusters are a minor fraction in the plume.}

The IBE and MPI processes were discussed in more detail in Chapter 3. IBE scales with the wavelength while MPI scales with the inverse of the wavelength.  Thus at 193 nm MPI is considered to be the more important mechanism for plasma formation, although MPI can also be a seeding mechanism for IBE since the latter is highly dependent on the ion (and inherently the electron) concentration in the plasma.

MPI is still quite improbable in the case of a carbon atom (ionisation potential (IP) = 11.26 eV) with 193 nm photons, since it involves a two photon excitation process.  However, this assumption may merit closer scrutiny in the case of both ArF and KrF laser ablation of carbon targets since two low lying metastable excited states of atomic carbon (the 2p²;¹D and 2p²;¹S states) coincidentally have strong one photon absorptions that fall within the respective excimer laser bandwidths.^25,26  Pappas et al.¹⁰ have highlighted the particularly good resonance between the 2p¹3s¹;¹P^o¬2p²;¹D transition at 193.09 nm and the peak of the ArF excimer laser output.  Given that the ¹D state of atomic carbon lies at an energy 1.263 eV above that of the ³P ground state, and assuming a typical surface vaporisation temperature T_s ~ 4500 K in the focal spot on the graphite target, simple thermodynamic considerations would suggest that ~2% of the ablated C atoms will be formed in the metastable excited state.  The 2p¹3s¹;¹P^o¬2p²;¹D transition must provide strong resonance enhancement to the two photon ionisation of these atoms in the plume; at the prevailing laser intensities this will be a very efficient process and greatly enhance the local electron and ion densities.

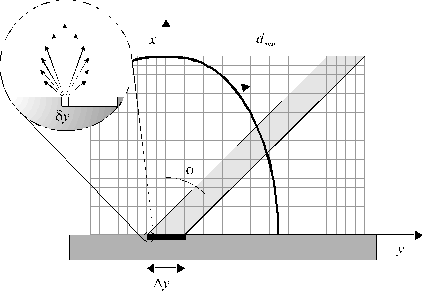
Both of the processes could attenuate the temporal lineshape of the incident laser beam in two different ways.  The IBE process would be expected to attenuate the trailing edge of the temporal laser profile since it is a cascade mechanism, which would be more prevalent at later timescales.  MPI would attenuate the highest intensity region of the temporal laser lineshape thus effectively broadening the lineshape.  This is shown in Figure 4.2.

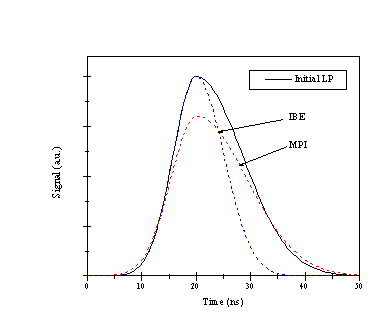
Figure 4.2: Schematic illustration of the different attenuations of the laser pulse profile by MPI and IBE in the plume (LP = laser pulse).  MPI will result in an attenuation of the peak intensity, while IBE will tend to attenuate the trailing edge of the laser pulse profile.

 

The temporal lineshapes of the laser light are given in Figure 4.3.  The lineshapes could be easily fitted to a split gaussian and analysed as such to eliminate the experimental noise on the curves.  The important figures to compare are FWHM values and the differences in total signal with change of fluence.  Important to note is that these are all relative measurements.  Measurements of the temporal laser lineshape without a target at higher fluences tended to saturate the detector while pulses at lower fluences (5 J/cm²) yielded a value ~17 ns FWHM.  The error bars on the FWHM are also limited by the sample rate of the oscilloscope (2.5 GHz) giving an accuracy of 0.4 ns.

 

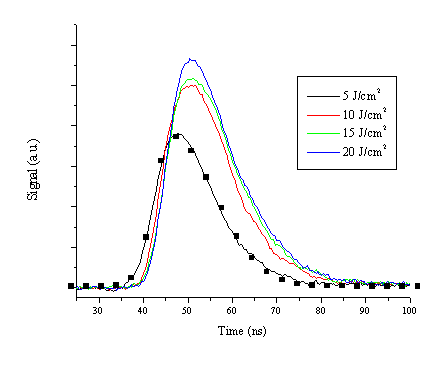
Figure 4.3: Experimentally monitored laser pulse profiles for four different fluences.  The black squares represent points of the fitting function used to fit the data recorded with a fluence of 5 J/cm².  Zero is not well defined for these transients, the oscilloscope was triggered from the rising edge of the temporal profile.

 

The results of the attenuation experiment are summarised in Figure 4.4.  The relative values of the FWHM (Figure 4.4(a)) do not show large differences, but the total signal shows a well-defined trend with increasing incident pulse energy (Figure 4.4(b)).  The FWHM variation suggests that the attenuation process is a convolution of both MPI and IBE, since the two attenuation mechanisms will affect the temporal lineshape in opposite ways.  The apparent relative decrease in the FWHM at the highest fluence might indicate a greater importance of IBE at higher fluences although the intrinsic error bars on the measurements (± 0.4 ns) are too high for this to be a quantitative conclusion.  The total detected signal levels out at fluences higher than 12 J/cm² indicating an increasing attenuation that could correlate with a cascade mechanism like IBE, in accordance with the figures obtained for the FWHM.  Comparing the values of the integrated detected signal for an incident fluence of 20 J/cm² with those for 5 J/cm² indicates that the plasma exhibits an additional absorption of 60% at the highest fluence.

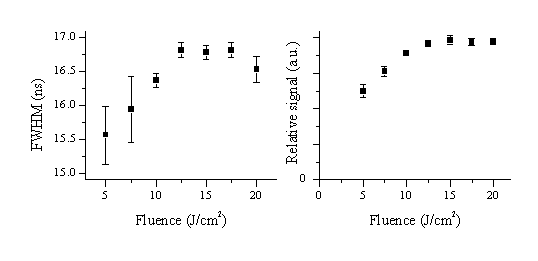
Figure 4.4: (a) The FWHM and (b) the total signal of the recorded laser profiles as a function of the fluence (5-20 J/cm²) of the incident laser light. The origin (0,0) is included in the latter graph as a reference.  The error bars are the standard deviations taken from four independent measurements.

 

The observed behaviour can be rationalised as follows.  The laser photons cause the crystal lattice to heat up and emit atoms and ions.  The percentage of the total material flux ejected as ions as a result of a thermal evaporation mechanism is insignificant.^[22]  The main ion generating process in this initial regime will be MPI, given the small initial ionisation fraction, the dependencies of the various possible ion forming processes on the experimental conditions and the fact that the MPI process is resonance enhanced.  This, in turn, will lead to an increase in the local absorption due to electron-neutral and, particularly, electron-ion inverse Bremsstrahlung which, having a continuum spectrum, can interact with all photons within the ArF laser bandwidth.  Thus the initial resonance enhanced two photon ionisation of metastable C (¹D) atoms is considered to act as a localised, and highly non-linear, 'seed' for further absorption and ionisation processes.  Quantitatively, the results indicate that plasma absorption of the laser light becomes a prevalent mechanism for plume heating at fluences above 12 J/cm².

These results can be compared and contrasted with recent results for Poly-Methyl Methacrylate (PMMA) and Poly-Imide ablation (PI).³⁴  The ablation of polymers is considered to be a much purer photoablation ^[23], with direct excitation of chromophoric groups in the lattice, which makes straightforward comparison impossible.  Nevertheless the deduced percentages of the incident laser light absorbed by the plume (45 % at a fluence of 4 J/cm², rising to 80 % at higher fluences (10 J/cm²)) is very comparable to the attenuation levels we deduce for graphite at fluences > 12 J/cm².

 

4.4. Optical emission of the ablation plume

 

4.4.1. Wavelength dispersed emission

 

The ablation plume arising in the 193 nm ablation of graphite in vacuum is clearly visible to the naked eye.  When viewed from above, at lower fluences (F ~ 12.5 J/cm²), the plume appears as a small volume of intense white plasma localised at the laser focus, and a more extensive diffuse green emission, which appears symmetrically distributed about the surface normal and fills the major part of the forward hemisphere.  Occasional thin bright tracks originating from the focal volume with seemingly random trajectories are also evident.  These we attribute to incandescent sputtered macroparticles (see also Chapter 6).^[24]  At higher F, these emissions are supplemented by a shaft of purple fluorescence, also originating from the focal volume.  This emission appears to be distributed asymmetrically about the surface normal.  Indeed, when the long axis of the rectangular laser output is parallel to the viewing axis (i.e. along z) the purple shaft appears to follow an axis that approximately bisects the laser propagation axis and the surface normal.  These laser fluences fall in the regime characterised by significant absorption of the laser light by the ablated plume as indicated in section 4.3.

 

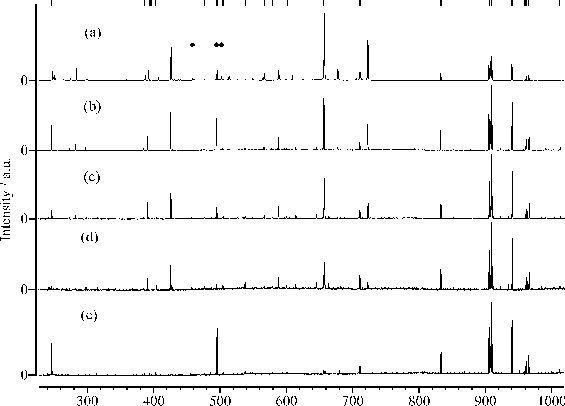
Figure 4.5: Wavelength dispersed spectra of the plume emission accompanying 193 nm PLA of graphite in vacuum, using 20 J/cm² laser pulses incident at 45° to the surface normal and with the long axis aligned vertically.  Spectra (a)-(d) were recorded at q ~+22° to the surface normal, at distances d = 3, 7, 12 and 20 mm from the focal region, respectively. (e) is taken at d = 7 mm and q ~-22° axis.  C emission lines are indicated by the comb above (a), ¨ indicates lines appearing in second order, while all other lines are associated with C⁺ or C²⁺ ions as described in the text.

 

Figure 4.5 shows several low resolution (Dl = 0.8 nm) wavelength dispersed emission spectra covering the range 225-1025 nm recorded from localised regions of the ablation plume resulting from 193 nm PLA of graphite in vacuum, using 20 J/cm² laser pulses incident at 45° to the surface normal and with the long axis of the laser output aligned vertically.  Spectra (a)-(d) were recorded along the shaft of purple emission, i.e. at q ~+22° to the surface normal (positive q corresponds to angles on the same side of the surface normal as the laser propagation), viewing at distances d = 3, 7, 12 and 20 mm from the focal region.  Contrast spectrum (b) with that shown in (e), which was also recorded at d = 7 mm but now monitoring along the q ~-22° axis. 

Each such spectrum was obtained by joining three overlapping 300 nm sections recorded using the Instaspec IV system (30 laser shot accumulations).  The displayed spectra have not been corrected for the wavelength dependence of the quartz fibre bundle transmission, the grating reflectivity, or the efficiency of the CCD array detector; the overall detection sensitivity peaks at ~620 nm and is at least four times lower at the two extremes of the range displayed.

All features in these spectra can be assigned in terms of monatomic carbon species - neutrals and cations.  Indeed, spectrum (a) exhibits all of the more intense documented ^{[25],[26] transitions of C and C+} that lie in this wavelength range (suggesting a lack of specificity in the excited state production process), while only emissions associated with neutral C atoms are apparent in spectrum (e).  Additional lines, e.g. at 501.76 nm, 495.76 nm and 459.45 nm, are transitions appearing in second order associated with, respectively, the C⁺(2p³;²D^o ® 2s¹2p²;²P) multiplet at ~251.1 nm, the 2p¹3s¹;¹P^o ® 2p²;¹S transition of atomic C at 247.86 nm, and the 2p²;¹D ® 2s¹2p¹;¹P^o transition of the C²⁺ dication at 229.69 nm.  Comparing such spectra recorded at a range of positions in the plume and at a range of incident fluences reveals that:

 

(i)                  The C²⁺ feature is observed only at small d and at the highest F.

(ii)                The C⁺ emission line intensities are greater (relative to those associated with neutral C atoms) at smaller d and at higher F.

(iii)               Only neutral C emission lines are detected in regions remote from the focal spot and the purple shaft (e.g. at d ³ 3 mm for all q £ 0°).

 

Findings (i) and (ii) are in good accord with conclusions reached in a previous OES study of 193 nm laser ablation of graphite,⁷ though we also observe many emission lines at l >600 nm not observed in the earlier work, presumably because of detector insensitivity at these longer wavelengths.  In accord with previous studies,^{7,9,[27] we see no emission attributable to electronically excited molecular species in any of these spectra, though the characteristic Swan band (d3}P_g®a³P_u) emission of C₂ is clearly visible when the ablation is carried out in background pressures of <1 Torr (<133 Pa) of He or Ar.^[28]  OES, of course, only provides information about the (generally small) fraction of material that happens to be present in states that decay radiatively. 

Nonetheless, preliminary QMS measurements performed with this apparatus ²⁸ of the energetic positively charged component of the plume generated by 193 nm PLA of graphite in vacuum reinforce the view that the plume is predominantly atomic in composition.  These QMS investigations of the ionic fraction reveal just three peaks - a dominant peak with mass to charge (m/z) ratio 12 and weak features with m/z 13 and 6, which are most readily attributed to ¹²C⁺, ¹³C⁺ and ¹²C²⁺ ions, respectively (appendix 2).  

 

4.4.2. Time resolved imaging of species specific emissions

 

The time evolution of the various emissions was investigated by time gated CCD imaging to measure TOF transients of wavelength selected emissions through a spatially localised and defined viewing column. 

 

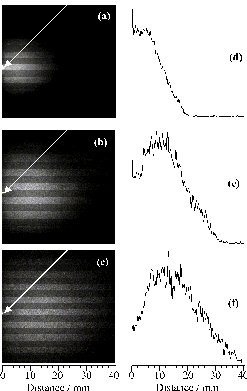
Figure 4.6: CCD images of neutral C atom emission with l > 780 nm centred at (a) 430 ns, (b) 630 ns and (c) 830 ns (Dt=100 ns), following 193 nm PLA of graphite in vacuum.  0 mm defines the front face of the graphite target, and the laser pulse is incident at 45° to the surface normal as indicated by the white arrow, with its long axis aligned along z.  (d)-(f) show the corresponding plots of emission intensity versus distance along the surface normal (x).

 

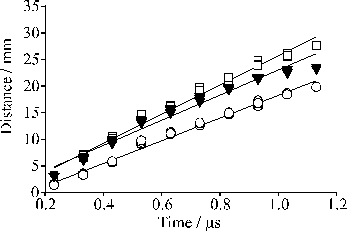
Figure 4.6(a)-(c) displays time gated (Dt =100 ns) intensified CCD images obtained by monitoring all detectable emission transmitted by a long wavelength band pass filter opaque to l < 780 nm, recorded at three different times, following 193 nm PLA of graphite in vacuum.  Again, the long axis of the laser output was aligned vertically in the laboratory frame.  0 mm defines the front face of the graphite target, and the laser pulse is incident at 45° to the surface normal.  Analysis of the wavelength dispersed spectra (Figure 4.5) reveals that neutral C atoms are the sole carriers of such emission. Obviously, the measured images are 'squashed' 2-D projections of a 3-D cloud of emitting particles.  Nonetheless, it is instructive to analyse such images in order to gain some measure of the radial velocity distribution.  The right hand panels (d)-(f) show plots of emission intensity versus distance along the surface normal which, in this case, corresponds to the axis of maximum emission intensity.  Figure 4.7 shows a plot of the median (i.e. centre-of-gravity) intensity position of a series of such images taken every 0.1 ms after the laser pulse versus delay time; the gradient of the line of best fit implies a propagation velocity for the emitting neutral C atoms, v_n = 21 ± 1 km/s.  Image analysis also allows estimation of the full width half maximum (FWHM) of the measured emission intensity profiles along any user selected slice, e.g. parallel and perpendicular to the propagation axis.  Dispersion velocities dv_x = 28 ± 1 km/s and  dv_y = 24 ± 1 km/s were derived in this way, suggesting that the emitting C atom component within the ablation plume is propagating and expanding at comparable rates.

 

Figure 4.7: Medians of the intensity distributions along x (O), and FWHMs (dv_x (¨) and dv_y (▼)), derived from time gated CCD images of the neutral C atom emission such as shown in Figure 4.6(a)-(c), recorded as a function of delay time after the laser pulse.  The gradients of the lines of best fit give one measure of the propagation and dispersion velocities for the emitting neutral C atoms, v_n = 21 ± 1 km/s, dv_x = 28 ± 1 km/s, dv_x = 24 ± 1 km/s.

 

Such behaviour should be contrasted with that displayed by the emitting C⁺ ions, which we choose to monitor via the 4f¹;²F^o ® 3d¹;²D transition at ~426.71 nm.  This closely spaced doublet emission was isolated by imaging through a narrow band interference filter with peak transmission at 426.7 nm and 3 nm transmission FWHM.  As Figure 4.8 shows, the C⁺ emission following irradiation of the graphite target with the beam incident at 45° to the surface normal is concentrated in a faster moving plasma ball that evolves along an axis roughly midway between the laser propagation axis and the surface normal. As with the neutral C atom emissions discussed above, analysis of such time-gated images provides a measure of the median propagation velocities of the emitting C⁺ ions (₊ ~ 40 ± 1 km/s along the q = +22° axis) and of the dispersion velocities parallel and perpendicular to this axis (dv_par = 11 ± 1 km/s and  dv_perp = 16 ± 1 km/s, respectively). 

 

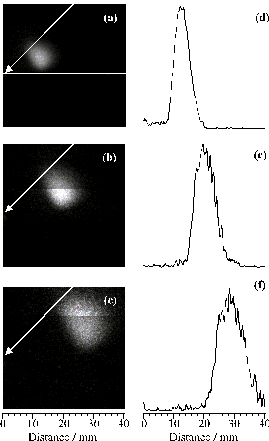
Figure 4.8: Time-gated (Dt =100 ns) intensified CCD images of the 426.71 nm C⁺ emission accompanying 193 nm PLA of graphite in vacuum.  The three time windows shown are as in Figure 4.6 and, as in that figure, 0 mm defines the front face of the graphite target, and the laser pulse is incident at 45° to the surface normal and with its long axis aligned along z.  (d)-(f) show the corresponding plots of emission intensity versus distance along the q = +22° axis.

 

Figure 4.9 shows images taken at three other angles of incidence (-11°, 30° and 60°).  These serve to confirm the generality of the observation that the C⁺ emission accompanying 193 nm ablation of graphite in vacuum (with the long axis of the laser output aligned along z) expands along an axis that is approximately centred on the angle bisecting the laser propagation axis and the surface normal.  Previous studies^6,[29] of pulsed laser ablation of graphite at both 193 nm and 248 nm have noted the different propagation characteristics of the C⁺ and C emission components, but the directionality of the ball of C⁺ emission was less evident. 

 

Figure 4.9: Time-gated intensified CCD images (Dt =100 ns centred at a delay of 430 ns) of the 426.71 nm C⁺ emission accompanying 193 nm PLA of graphite in vacuum, recorded at (a) 11°, (b) 30° and (c) 60°.  As in Figure 4.6, 0 mm defines the front face of the graphite target, and the long axis of the output is along z.  Each image has been cropped top and bottom for compactness of display.

 

Figure 4.10 provides a further exploration of this oversight.  The ball of C⁺ emission observed when the laser is incident at q = 45°, but with the long axis of the output now aligned along y (i.e. rotated so as to be perpendicular to the observation axis), is seen to propagate along q ~10° (i.e. much closer to the surface normal).  Analysis of a time sequence of such images yields a mean propagation velocity, ₊ ~40 ± 1 km/s along the q = 10° axis, and dispersion velocities parallel and perpendicular to this axis (dv_par = 17 ± 1 km/s and  dv_perp = 11 ± 1 km/s), very similar to those measured with the laser pulse output aligned along z.  

 

Figure 4.10: CCD images of the 426.71 nm C⁺ emission, recorded with the intensifier time gate (Dt=100 ns) centred at (a) 430 ns, (b) 630 ns and (c) 830 ns, following 193 nm PLA of graphite in vacuum with the laser pulse incident at 45° to the surface normal.  Again, the various images have been cropped top and bottom for display purposes and 0 mm defines the front face of the graphite target but, in contrast to Figure 4.9, the long axis of the laser output is now aligned along y (i.e. perpendicular to the observation axis).

 

Such species selective, time lapse images of the plume provide one direct, and very visual, means of monitoring the ablation plume and of estimating the propagation velocities of various of the constituents within the plume.  These data can be compared with TOF measurements of wavelength selected emissions monitored using the fibre bundle, Spex monochromator and a fast PMT.²⁸  These measurements yield propagation velocities of 42 ± 1 km/s for the C⁺ cations (measured for the 426.7 nm transition) and the C²⁺ dications and a propagation velocity of 33 ± 1 km/s for the C atoms.

The propagation velocities for the C⁺ ions obtained by both methods are in good agreement with those estimated by Puretzky et al. ²⁹ from analysis of time gated images of the fastest component in the total emission resulting from ArF laser ablation of graphite in vacuum.  The value recorded for the neutral carbon atoms are somewhat greater than that deduced from the time gated imaging studies shown in Figure 4.6 but still slower than the more localised C⁺ ion emission.  Before discussing the significance, and some of the limitations, of such OES studies, we first consider another type of measurement which can provide complementary information about the motion of positively charged particles in the expanding plume.

 

4.5. Faraday Cup Measurements

 

Figure 4.11(a) displays TOF transients of the positively charged material within the ablation plume, obtained using laser fluences of 5, 10, 15 and 20 J/cm², each incident at 45° to the surface normal, measured using the Faraday Cup detector located on the x axis with its front face at a distance d = 421.7 mm from the target. 

 

Figure 4.11: (a) TOF transients of the positively charged component of the ablation plume resulting from 193 nm PLA of graphite, in vacuum, using pulse energies of 5 (O), 10 (¨), 15 (D) and 20 J/cm² (Ñ).  The solid curve through the 15 J/cm² profile shows the result of a least squares fit in terms of Equation (4.1), (b) shows the velocity distributions that derive from the experimental TOF profiles.

 

The solid curve through the TOF profile recorded with 15 J/cm² incident pulses serves to illustrate that the TOF profiles are each well described by a shifted Maxwell-Boltzmann velocity distribution of the form:

 

n(x,t) µ t-5 exp

(4.1)

 

where n(x,t) is the space- and time-dependent particle density, t is the TOF, and T (the local equilibrium temperature) and u (the flow velocity parallel the surface normal) are parameters to be floated in the fit.  Such a function is generally assumed to provide a valid description of the TOF profile of ablated material in cases where a Knudsen layer is formed.^{19,[30]  Given previous estimates 8} (from target mass loss measurements) that the C atom removal rate in these experiments is ~10¹⁵ pulse^-1 when using 20 J/cm² incident pulses, together with representative collision cross-section and velocity values of ~0.2 Ų and 40 km/s, respectively, the requisite few collisions deemed necessary for Knudsen layer formation close to the surface will occur within the first few nanoseconds of the laser pulse.  A more detailed discussion on the functional form of Equation (4.1) can be found in Chapter 3.

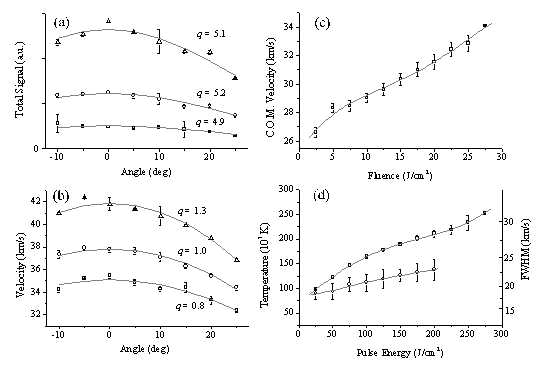
For analysis of the velocity profiles we define the most probable velocity (v_mp) as the velocity corresponding to the peak signal and the mean velocity (v₊) as the velocity separating the slower and faster halves of the total integrated signal.  Comparing these two defined velocities Figure 4.12(a) gives an indication of the anisotropy of the velocity distribution.  The velocity distributions that derive from these TOF profiles, displayed in Figure 4.11(b), show that both the total ion signal and the mean, v₊, of each velocity distribution scale with increasing incident energy.  These trends are summarised in Figure 4.12, where the mean ion kinetic energy has been calculated on the assumption that the charged particles have m/z 12. 

 

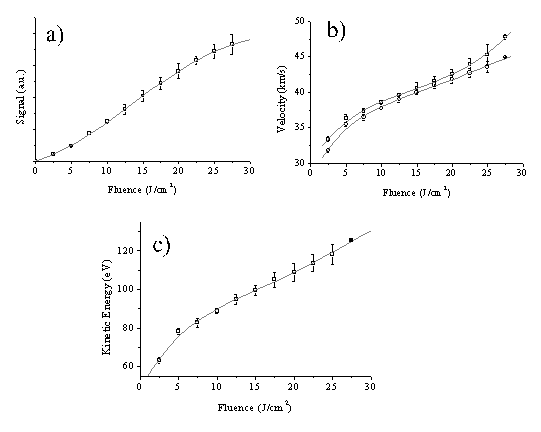
Figure 4.12: Plots illustrating the variation of (a) total ion yield, (b) v_mp (□) and v₊ (O), and (c) the mean ion kinetic energy with pulse energy. The error bars in (a) show the reproducibility of five separate measurements of relative signal strengths as a function of pulse energy, each set of which has been arbitrarily normalised to unit signal at F = 7.5 J/cm², while those in (b) and (c) are standard deviations (1s) of the absolute velocities determined from, typically, five measurements at each energy.  The solid curves in each plot are fourth order polynomial fits to the various data sets.

 

Interestingly, the plot of kinetic energy versus incident pulse energy (Figure 4.12(c)), though roughly linear, has a much shallower slope than that reported previously in the case of 308 nm ablation of graphite in vacuum.¹⁹  Figure 4.12(a) reveals ion production at very low incident fluences, in marked contrast to the OES measurements in which formation of electronically excited C⁺ ions (i.e. the purple shaft) was evident only above a certain threshold energy, but the deduced velocities (e.g. v₊ = 42.5 ± 1 km/s for incident 20 J/cm² pulses) match well with those derived from the OES studies of C⁺ emission.  However, the CCD imaging studies also showed the distribution of emitting C⁺ species to be highly asymmetric about the surface normal - at variance with previous ion probe studies which suggested a far more uniform recoil distribution of the total ion flux.⁸ 

 

Figure 4.13: Plots showing: (a) the angular variation of the total positive ion signal arising in the 193 nm PLA of graphite in vacuum, using fluences of 5 (¨), 10 (O) and 20 J/cm² (D) and (b) the angular variation of the corresponding v₊ values.  The smooth curves through the points are fits in terms of cos^qq distributions, with the best fit q value indicated in each case; (c) and (d) show, respectively, the deduced centre of mass velocity, u, and the velocity dispersions parallel, dv_x (¨), and perpendicular, dv_y (O), to the surface normal, each as a function of incident pulse energy.  The solid lines in these two panels are fits (using fourth order polynomials) to the data.  The error bars are deduced as in Figure 4.12.

 

This paradox has been investigated further using the Faraday cup assembly.  Experimental constraints mean that the axis along which the laser is incident and the ion detection axis had to be held constant.  To investigate the variation in scattered ion flux with q (i.e. relative to the surface normal), it was thus necessary to vary the angle of incidence on the target, by rotating the target assembly about the z axis, and measuring TOF transients such as those shown in Figure 4.11, as a function of both the laser pulse energy and its angle of incidence.  Inevitably, this procedure must cause some change in the footprint of the focal spot on the target, and thus in the incident fluence at any given pulse energy.  Nonetheless, as Figure 4.13(a) shows, the angular distribution of the total ion flux measured in this way, at all incident fluences, peaks at q = 0° (in contrast to the OES observations) and conforms to a cos^qq distribution with q ~ 5, thereby reinforcing previous conclusions²⁴ that the distribution of the total ion flux distribution is considerably more isotropic than that of the C⁺ ions evident in OES. 

Given this grid of measured TOF spectra it is also possible to determine the way in which the velocity distribution varies with scattering angle.  Knowing d, it is possible to transform any measured TOF profile into the associated velocity distribution; Figure 4.13(b) shows that the median velocity, v₊, also peaks at q ~ 0° and exhibits an angular dependence that scales as cos^qq, with a best-fit q value that rises from ~0.8 (for 5 J/cm² pulses) to ~1.2 (when using 20 J/cm² pulses).  It is also possible to fit each measured TOF profile in terms of a function analogous to Equation (4.1) but which now, since we are concerned with material ejection along axes other than the surface normal, involves velocity components both parallel and perpendicular (y) to x, i.e.

 

n(xi,yi,t) µ At-5 exp

(4.2)

 

Only T_y was floated when fitting TOF spectra recorded at q ¹ 0°; u and T_x were clamped at the values determined from analysis of TOF spectra of ions ejected along the surface normal (i.e. using Equation (4.1)) at the same incident pulse energy.   Best-fit values of u, T_x and T_y, and their variation with incident pulse energy, are shown in Figure 4.13(c) and (d).  The corresponding full width half maximum (FWHM) velocity spreads parallel and perpendicular to the surface normal, dv_x and dv_y, are deduced from the relationship

 

dvx(y)  =

(4.3)

 

which follows from assuming that the velocity spreads in the x and y directions may be described by Gaussian functions.  Reviewing these fits, and the plots shown in Figure 4.12 and Figure 4.13, we note for future reference that the total ion distribution in the plume resulting from 20 J/cm² excitation is well described by a shifted Maxwell-Boltzmann distribution propagating along the surface normal with a flow velocity, u ~ 35 km/s, and dispersion both parallel (dv_x) and perpendicular (dv_y) to this axis of ~25 km/s (FWHM).  These values will be used later, in a simple model designed to account for the observed asymmetric C⁺ emission.

 

4.6. Discussion of the results and model

 

Three different strategies, two based on OES ²⁸, the other employing a Faraday cup, return similar values for the propagation velocity of the ionic component within the plume arising in the pulsed 193 nm laser ablation of graphite in vacuum.^[31]  Estimates of the propagation velocity of the neutral atomic C component determined by the two forms of OES show more variation, but consistently indicate that ₊ > _n, in accord with previous studies.^6,8,29  Such observations are consistent with contemporary models of UV laser ablation in which the laser pulse induces localised surface excitation and rapid heating, leading to photo- and thermionic electron emission closely followed by ejection of positive ions, which are accelerated out of the focal volume as a result of Coulombic attraction (by the expanding electron cloud) and repulsion (by other ions at smaller d) before reaching some terminal propagation velocity. ^[32]  Species ejected into the vacuum as neutrals are not subject to this Coulombic acceleration, whilst neutrals that result from gas phase ion-electron recombination in the denser (early time) regions of the plume will only experience such acceleration prior to neutralisation and thus attain a lower terminal velocity.  More careful inspection, however, reveals other differences between the various measurements.  Most notably, the CCD imaging studies suggest a far more localised distribution of emitting C⁺ species (both in the radial and angular co-ordinates) than is indicated by either the present, or previous,⁸ ion probe measurements.

Here we concentrate attention on possible mechanisms for producing the electronically excited species monitored via OES and, in particular, the origin of the localised shaft of C⁺ emission.  The radiative lifetimes of the various excited species are far shorter than the timescales over which emission is observed.  Thus the emission observed at larger d must be from excited states that are populated post-ablation, in the gas phase, well after cessation of the pulsed laser excitation.  Electron impact excitation (EIE) during plume expansion is one possible route for forming excited state species, the efficiency of which should fall with decreasing number density, and thus increasing d.  On this basis, EIE induced emission should be most efficient at small d, and thus favour the slower moving particles.  That being the case, OES might be expected to underestimate the actual plume propagation velocity.  However, the EIE mechanism also requires the electrons and the atoms/ions to be proximate.  Given that the electrons and ions have similar propagation velocities,⁸ both of which are greater than _n, it might follow that EIE would actually favour that sub-set of the total flux distribution that was propagating at similar speeds to the expanding electron cloud (i.e. the faster part of the neutral velocity distribution).  EIE of C atoms and C⁺ ions is generally spin conserving. ^[33]  Thus, if EIE is the major route to the observed emissions, the fact that all C and C⁺ emissions that fall within the monitored wavelength range are indeed observed (Figure 4.5) would imply the formation of both ground (triplet) and excited (singlet) C atoms in the ablation process.  However, many of the emissions originate from very energetic excited states - e.g. the ⁴P^o excited state of C⁺ responsible for the 432.2 nm and 359.1 nm emissions observed along the q = +22° axis at short d lies 25.98 eV above the ground state ion and 37.25 eV above the ground state of neutral carbon.  Such high levels of excitation are hard to reconcile with simple EIE induced by electrons propagating with mean kinetic energies in the meV range.  Neither does an EIE mechanism provide a particularly obvious explanation for the observed highly localised C⁺ emission.

Another mechanism for forming electronically excited species is electron-ion recombination (EIR).  This requires the presence of a third body to stabilise the recombination product, and should thus also be most important at small d.  EIR would encourage the conversion C²⁺ ® C⁺ ® C, in accord with the d dependence of these various species revealed by the OES studies.  EIR will favour formation of Rydberg states with high principal quantum number, n, since these recombination products require least energy transfer to the third body.  Many of these Rydberg states will be formed not just with high n but also high l (where l is the orbital angular momentum quantum number).  Given the Dl = ±1 selection rule associated with allowed radiative transitions, these species can only radiate by a cascade mechanism.  The initial steps in this cascade will involve Rydberg-Rydberg transitions at long wavelength; the spatial and temporal extent of the observed emission plumes would then reflect the time taken for the population in high n,l states to cascade down into the observed emitting levels.  The observation of emissions from excited states of both C and C⁺ involving ...ng¹ and ...nf¹ configurations and of sequences like:

 

      2s²6g¹;²G 2s²4f¹;²F^o 2s²3d¹;²D  2s²3p¹;²P^o 2s²3s¹;²S

 

in C⁺, encourage the view that radiative cascade accounts for the apparently delayed emission.  Clearly, wavelength resolved OES measurements at longer infrared wavelengths would help in confirming the importance of EIR processes. 

We now proceed to show how the localised C⁺ emission, its directionality, and its sensitivity to the orientation of the laser output, are all explicable in terms of EIR following laser-plasma (rather than laser-target) interactions; indeed, we will show that such observations are a signature of laser-plasma interactions.  To this end, we have implemented an approximate 2-D 'particle in the cell' type model which provides a rationale for the observed anisotropy of the C⁺ emissions, and identifies various parameters which will tend to enhance or degrade such anisotropic optical emission from ablation plumes.  Key features of the model are summarised in Figure 4.14.

 

Figure 4.14: Illustration of the 2-D model to account for the observation of asymmetric C⁺ emission. 

 

As in the experiment, the front face of the target lies in the yz plane, with the surface normal directed along x.  All of the present calculations consider material ejection just in the xy plane.  This space is partitioned into a mesh of 75 x 75 rectangular grid cells, chosen so as to span the entire 'volume' into which sputtered material may have travelled by the cessation of the laser pulse.  The pulse of laser radiation (of duration, t = 20 ns) is assumed to have a 'top hat' intensity distribution, in both space and time, and to be incident as a parallel shaft in the xy plane, at an angle f to the surface normal, so as to irradiate the target surface over a length distributed symmetrically about the point y = 0.  This length is treated as 21 identical pixels of width dy, each of which serves as a source of ablated particles.  All particles are treated as being identical, and each pixel within the length Dy is assumed to contribute equally to the total ablation yield.  In this simple model the ejected particle density from each pixel is distributed over 185 radial spokes, distributed uniformly throughout the angular range -90° < q < 90°.  

Modelling of the laser interaction is sub-divided into 20 time steps, each with dt = 1 ns, so as to span the entire laser pulse duration.  During the first time step, dt₁, a total of N₁ particles are ejected into the gas phase.  Each source pixel contributes equally to N₁, and each contribution is given an overall velocity distribution (defined relative to its particular cell origin) the same as that deduced from analysis of the ion yield arising when using 20 J/cm² pulses (i.e. u = 35 km/s, and with a Gaussian spread of 25 km/s (FWHM) in both the x and y directions.  Each particle is ascribed an associated density, r_i, which is initially set to unity.  This is necessary if, as here, the interest is in possible laser-plume interactions, since plume material in the column exposed to laser irradiation can attenuate the incident beam, and thus reduce the light intensity incident on the target and the ablation yield.^[34]  This attenuation is modelled using the Beer-Lambert expression,

 

I(d) = I0exp[-ar(d)(dmax - d)]

(4.4)

 

where the absorption coefficient, a, is assumed to be intensity independent, r = is the local density within a grid cell distant d from the focal region, and d_max is defined as in Figure 4.14.  In the limit that a ® 0, the incident beam suffers no attenuation and I(d_max) º I₀. 

During successive time steps, particles generated during all previous time steps will continue to propagate forward, and additional plume material will be produced as a result of the (attenuated) laser beam striking the target surface.  To allow for possible plume absorption, the density r in each grid cell is calculated at the end of each time step.  Equation (4.4) is then used to calculate the intensity I(d) incident on, and exiting from, each grid cell during the next time step.  Consider two neighbouring cells along a radius within the irradiated column at positions d_n and d_n-1 (d_n >d_n-1), containing respective densities r_n and r_n-1.  We define an excitation density E_n(t) for the former grid cell as

 

En(t) = {rn [I(dn) - I(dn-1)]}(t)

(4.5)

 

for the time step of interest and obtain a final, total excitation density for this cell via the summation .  Excitation decay is not included within the model.  After 20 ns all gas phase material production and excitation is assumed to cease, and the velocities of all particles can be propagated to longer time to compare with the experimental observations.

 

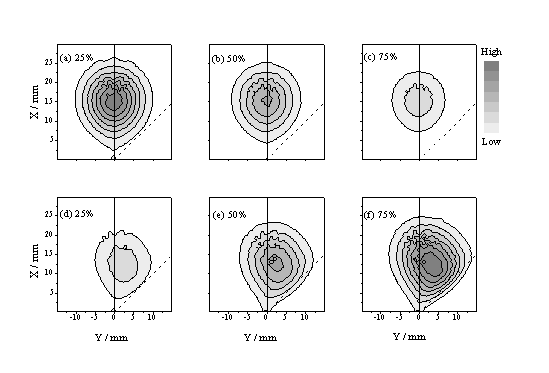
Figure 4.15: Linear grey scale plots illustrating the calculated spatial distribution of total ablated flux in the xy plane at t = 0.5 ms, for a laser pulse incident at 45° to the surface normal (indicated by dashed line), with Dy = 0.2 mm and Dt = 20 ns, assuming u = 35 km/s,  dv_x = dv_y = 25 km/s (FWHM) and three different 'strengths' of the absorption coefficient, a (such that the time integrated absorption corresponds to (a) 25, (b) 50 and (c) 75% of the incident light intensity, respectively).  Panels (d)-(f) show the calculated distribution of excitation density, r, within the plume given these same three absorption strengths.

 

Figure 4.15 shows - in the form of linear grey scale plots - the spatial distribution of total ablated flux in the xy plane predicted by this model at t = 0.5 ms, for a beam incident at 45° to the surface normal, with Dy = 0.2 mm and Dt = 20 ns, assuming u = 35 km/s, dv_x = dv_y = 25 km/s (FWHM) and three different 'strengths' of the absorption coefficient, a (such that the time integrated absorption corresponds to (a) 25, (b) 50 and (c) 75% of the incident light intensity, respectively). Clearly, plume absorption reduces the overall ablation yield, but its effect is more obvious in the complementary plots (Figure 4.15(d)-(f)) showing the predicted distribution of excitation density within the plume.  The anisotropy evident in these latter plots is reminiscent of that observed in the time gated CCD images of the C⁺ emission.  Figure 4.16 shows the predicted variation in the anisotropy of the excitation density with the angle of incidence, f, of the exciting light pulse ((a), top panel), the focal spot size, Dy ((b), centre panel) and the pulse duration ((c), bottom panel).  The qualitative trends evident in (a) and (b) accord with the experimental observations (Figure 4.9 and Figure 4.10).

 

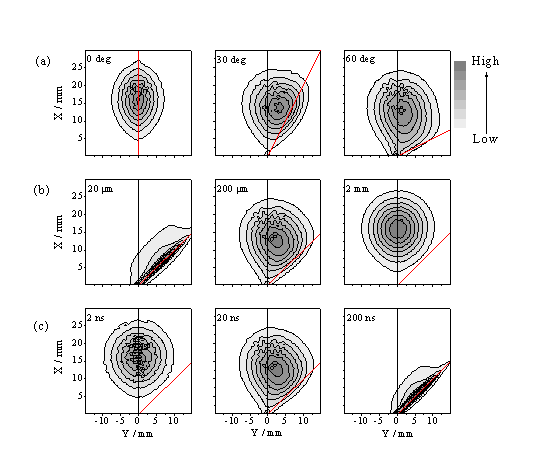
Figure 4.16: Predicted variation in the anisotropy, via grey scale plots, of the excitation density, r, with (a), (top panel) the angle of incidence, f, of the exciting light pulse (indicated by dashed line), (b), (centre panel) the focal spot size, Dy, and (c) (bottom panel) the pulse duration, Dt.  The default conditions apply for panel (b), 200 mm.

 

The model calculations support the view that asymmetric plume excitation will generally be most evident in experiments which (as here) involve laser pulses incident at an angle away from the surface normal, of long time duration, and that are tightly focused such that the focal spot size on the target in the viewing plane (Dy) is small compared to the distance (d_max) that material can travel during the laser pulse.  The simulations shown in Figure 4.16 indicate that the anisotropy will be reduced by expanding the size of the focal spot (as found experimentally - Figure 4.10), or by reducing the pulse duration.  A more critical comparison between experimental observation and the model predictions indicates that the latter tend to underestimate the observed asymmetry of the C⁺ emission.  Clearly, one contributor to this discrepancy is our use in the model of the 'asymptotic' particle velocity distribution, i.e. the distribution measured at long time, after formation of the Knudsen layer.  Within the context of the model as posed, however, excitation of gas phase material will be most efficient in the very early part of the laser pulse, before the Knudsen layer is fully developed.  Equation (4.2) with u ~ 0 should provide a better description of the initial velocity distribution of the ablated material in the early time, low-density, near collision-free limit.  The distribution of excitation density that results from assuming such a function is much more asymmetric.  Clearly, a better match with observation can be obtained by making u a time dependent function, but we are satisfied that the present more limited calculation suffices to demonstrate the source of the observed asymmetry of the C⁺* emission.

Figure 4.15 also serves to emphasise that such effects will be most evident where there is significant absorption by the plume.  Experiments employing longer duration, high energy pulses will tend to produce a longer, denser column of ablated material through which the beam must propagate to reach the target; plume absorption is likely to be more important.  Processes that might contribute to the attenuation of incident radiation by an ablation plume include scattering, and absorption - either resonant, or as a result of electron-neutral and/or electron-ion inverse Bremsstrahlung.^[35]  As shown in section 4.3, both of these latter processes play an important role in the whole laser ablation process.  The initial absorption can be ascribed to the resonance enhanced MPI process producing a relevant ionisation fraction.  This will, in turn, instigate the IBE process resulting in additional absorption of the laser light and local ionisation of the plume.  Thus the resonance enhanced two photon ionisation acts as a highly localised seeding mechanism for further ionisation.  This process will be prevalent in the regions of the plume receiving the highest and most prolonged photon flux.  These would be the regions identified as receiving the greatest excitation density in the simple model calculations reported above and, qualitatively at least, these correlate with the observed localised shaft of C⁺ emission.

4.6.1. Conclusions for the laser ablation plume characteristics

 

Electronically excited species (C atoms, and C⁺ and C²⁺ ions) in the plume accompanying 193 nm PLA of graphite in vacuum have been investigated by wavelength, time and spatially resolved OES, while the positively charged component has also been investigated using a Faraday cup detector.  In addition, the attenuation of the laser light by the ablation plume has been studied by directly measuring and comparing the temporal profiles of the laser pulse after propagating through the ablation plume for different fluences.

The temporal and spatial extent of the optical emissions are explicable if it is assumed that the emitting species result from electron-ion recombination processes, and subsequent radiative cascade from the initially formed high n,l Rydberg states.  The C neutral emission is observed to be distributed symmetrically about the surface normal, but the C⁺ emission is seen to be localised in a rather narrow solid angle between the laser propagation axis and the surface normal.  However, the complementary Faraday cup measurements of the ion yield and velocity distributions, as a function of scattering angle and incident pulse energy, indicate that the total distribution of positive ions also peaks along the surface normal.  The velocity distributions so derived are used as input for a simple two dimensional model which provides a rationale for the observed anisotropy of the C⁺ emission in terms of preferential multiphoton excitation and ionisation of C species in the leading part of the expanding plasma ball that are exposed to the greatest incident 193 nm photon flux, and subsequent electron-ion recombination and radiative decay.  The attenuation experiments studied with the laser beam incident on the surface normal indicate a strong absorption of the laser light at fluences above 12 J/cm².  This is the fluence regime where a bright purple plasma ball becomes prevalent in the optical emission.  The results support an initial ion creation mechanism involving resonance enhanced multiphoton ionisation with, at higher fluences, sequential photon absorption by the plasma resulting from electron-ion IBE.  The reported results from the different applied techniques are in very good agreement with each other and with results reported in related studies.^6,7 

 

4.7. Deposition of Diamond Like Carbon films

 

The deposition of DLC films was the subject of previous studies in our group; ²⁸ these results are summarised so as to provide a complete story.  The films were typically deposited from graphite, although we have also investigated DLC film production via ablation of CVD diamond.²⁴  A previous optical emission study of the ablation plumes from both target materials revealed that the ablation characteristics of the materials are very similar.  This is explained by assuming that the incident laser light induces local melting of the graphite and the CVD diamond target surfaces prior to ablation.  Thus the CVD diamond surface undergoes a 'graphitisation' and, thereafter, shows the same ablation characteristics as graphite itself.²⁴

The films were characterised by UV-VIS and Raman spectrometry and their field emission characteristics were investigated.

 

4.7.1. Deposition of DLC films

 

193 nm laser fluences required for production of high quality DLC films from graphite were determined to be in the range of 12.5 J/cm² and 25 J/cm².  Obtaining sufficiently sharp SEM cross-sectional images of the DLC films produced in this work to allow reliable estimation of the film thickness proved difficult.  However, guided by our previous studies of the 193 nm PLA of graphite in vacuum ²⁴ (which suggested deposition rates of ~7 pm pulse^-1), we estimate that the 'typical' film deposited here using 20 J/cm² pulses, 10 Hz repetition rate and 15 minutes duration had a thickness of ~50 nm.  SEM imaging showed severe delamination of films deposited from both graphite and CVD diamond targets when using longer durations, or higher pulse energies, as shown in Figure 4.17.

 

Figure 4.17: SEM of film delamination, film deposited at 20 J/cm² and 30 minutes.

 

The deposited films are characterised with UV-VIS and Raman spectrometry.  Typical spectra obtained by the two techniques are given in Figure 4.18.  The results show that the films are typical DLC films, and their characteristics can be compared with the studies given in references 7.

The UV-VIS spectrum shows that absorption of the film stretches out into the visible region (E < 3 eV) and that the DLC films do not exhibit a well-defined optical band gap.  A general procedure to estimate the band gap involves extrapolation of the long wavelength part of such plots of absorption coefficient versus energy (or frequency) and determining the energy at which this trend-line intercepts the energy axis.  It is clear that almost any band gap value could be obtained by extrapolating the appropriate part of an absorption spectrum such as shown in Figure 4.18(a).  Such UV-VIS spectra give convoluted information about the refractive index and the extinction coefficient of the material.  Ellipsometry offers a better method for determining these two quantities directly.  Ong et al. ⁷ have reported values of 2.1 - 2.3 eV for the optical band gap measured by ellipsometry for DLC films deposited under similar conditions to those used in the present work.

 

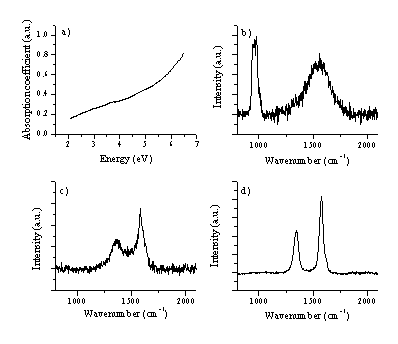
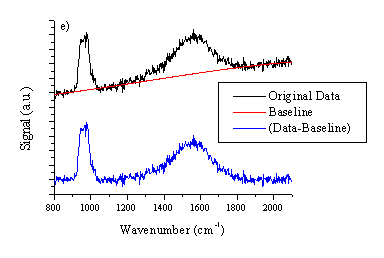
Figure 4.18: (a) typical UV-VIS spectrum of a film deposited from graphite on a quartz substrate at 25 J/cm².  Typical Laser Raman spectra, at an excitation wavelength of 514 nm of (b) the deposited film (c) the irradiated part of the graphite target and (d) the virgin graphite target as comparison. The total signal in (c) and (d) are plotted on the same vertical scale for comparison.  All the Raman spectra are baseline corrected, the procedure is shown in (e).  The peak at 960 cm^-1 in (b) is a feature associated with the Si substrate.

 

The Raman spectrum of the deposited film material is given in Figure 4.18(b) together with Raman spectra for graphite, pre- and post- ablation (c) and (d).  The spectrum taken from an irradiated graphite surface is distinctively different from that of the virgin graphite surface given for comparison.  The former shows clear broadening, reflecting disordering of the lattice structure.  This we attribute to localised melting of the graphite lattice under the influence of the high photon flux, though it should be noted that some redeposition of sputtered carbon atoms and ions occurs also, resulting in deposition of a thin DLC film on the target surface.

The Raman spectrum in Figure 4.18(b) is consistent with good quality hydrogen-free DLC, the peak around 960 cm^-1 is due silicon in second order (fundamental frequency ~520 cm^-1).  Quantification of these films was the subject of a more involved earlier study,²⁸ in which the DLC features were fitted to a Breit-Wigner-Fano lineshape (as discussed in reference [36]) to yield estimates of the sp³ fraction in the deposited films of > 60 %. 

As mentioned previously we also compared characteristics of the films deposited from 193 nm ablation of graphite and CVD diamond.  Figure 4.19 shows six laser Raman spectra.  (a) and (b) are of the as-grown free-standing CVD diamond and the high density graphite targets, respectively, (c) is of the focal area on the CVD diamond film surface post-ablation, while (d) and (e) show spectra of the DLC films grown on Si by PLA of these respective targets.  These five spectra were all recorded using 488 nm Ar⁺ laser excitation.  (f) displays a Raman spectrum of the same film as in (e), but recorded using 325 nm excitation.  Clearly, laser Raman spectroscopy of the deposited DLC films ((d) and (e)) provides yet more support for the view that there is little difference in the ablated material resulting from 193 nm irradiation of graphite and CVD diamond.  Some rationale for this finding comes from comparing spectra (a), (b) and (c).  The strong 1332 cm^-1 peak in (a) highlights the high quality of the CVD diamond surface, yet post-ablation (spectrum (c)) laser Raman spectroscopy shows little evidence for diamond.  All of the present observations are explicable by assuming that the initial stages of the PLA of CVD diamond in vacuum at 193 nm involve very rapid, localised surface graphitisation prior to material injection into the gas phase.

 

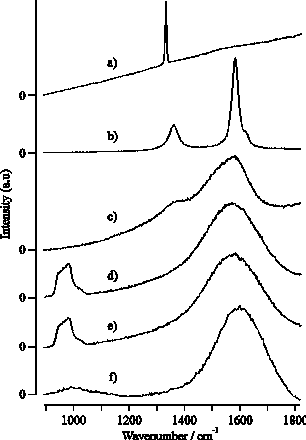
Figure 4.19: Raman spectra taken using 488 nm Ar⁺ laser excitation of (a) and (b) a virgin CVD diamond and graphite target, respectively, (c) the laser irradiation region of CVD diamond post- ablation, (d) and (e) films grown from CVD diamond and graphite, respectively and (f) the same film as (e) but the Raman spectrum is recorded with 325 nm laser excitation wavelength.

 

The differences between spectra (e) and (f) merit comment.  The strong feature centred in (e) at a Stokes shift of ~965 cm^-1 is a signature of the Si substrate.  The relative showing of this peak decreases with decreasing excitation wavelength (see also reference [37]), reflecting the increasing absorption coefficient of the deposited DLC coating at shorter wavelengths and the consequent reduction in the penetration depth achieved by the Raman exciting laser.  Closer inspection of these spectra, and of those taken previously for similar DLC films using 632.8 nm He-Ne laser excitation,^[38] reveals a noticeable and systematic shift in the peak of the broad asymmetric Raman profile traditionally associated with DLC, from ~1485 cm^-1 (632.8 nm excitation), through ~1560 cm^-1 (488 nm, (e)) to ~1595 cm^-1 (325 nm, (f)).  This suggests that, as is widely recognised for the case of polycrystalline CVD diamond, the detailed form of the Raman spectrum obtained for any given DLC film will be sensitive to the excitation wavelength used.^[39]

 

4.7.2. Field emission characteristics

 

Figure 4.20 shows measurements of emission current (I) as a function of bias voltage (V) for DLC films grown from both CVD diamond and graphite targets.  Such I-V curves were measured by ramping V up and down, repeatedly (sweep rate ~25 V s^-1); the reproducibility improved after the first few up-down cycles, but SEM analysis revealed that this 'conditioning' does affect the film morphology in the immediate vicinity of the emission sites.  An SEM image illustrating surface modification after field emission is given in Figure 4.21.  The surface shows severe damage but, as can be derived from the SEM picture, the damaged area shows better conductivity than the deposited film (the damaged area is brighter), indicating better transmission of electrons to the surface for field emission.

 

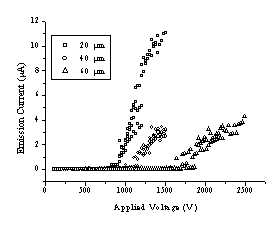
Figure 4.20: I-V curves for hydrogen-free DLC films grown on Si(100) by 193 nm PLA of (a) CVD diamond and (b) graphite obtained using 20 (o), 40 (O) and 60 mm (ê) anode-surface separations.

 

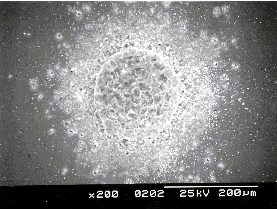
Figure 4.21: SEM of emission spot on a hydrogen-free DLC film grown by 193 nm PLD from a graphite target after field emission testing.

 

Measurements were made at three different anode-surface separations (20, 40 and 60 mm), at several sites on each film, and for at least two films deposited from each target material.  The DLC films derived from these two sources show very similar threshold voltages (50 V/mm) but, once above the threshold, films grown from CVD diamond appear to show a steeper slope, implying larger dI/dV.  Such behaviour may correlate with the density of larger (>1 mm wide) macroparticles in the film, which both optical microscopy and SEM images suggest is considerably higher in the case of the film deposited from CVD diamond.  Such a finding, which at first sight appears counter-intuitive given the proposed mechanisms for macroparticle ejection and the higher density and lower porosity of diamond, might well be dependent on the CVD diamond growth rate.  Diamond samples such as those used here, deposited at high growth rates using a plasma jet, are likely to contain more voids (and thus trapped gas pockets) than the smaller grain size films produced in most low power CVD reactors.

 

4.7.3. Deposition of C:S films

 

The deposition of sulphur containing DLC films (henceforth C:S films) at room temperature was also attempted.  The main challenge encountered in this part of the project was the target configuration.  The first attempts to make a C:S containing target involved cold pressing a mixture of graphite and sulphur powder.  Even at high pressures (~ 10 metric tonnes/cm²) this mixture remained as a powder.  The powder could be transformed to a solid by adding adamantane to the mixture, but adamantane has a high vapour pressure and the resulting disk fragmented when placed under vacuum. Hot pressing of the powders was not considered to be a viable production route, because of the huge differences in melting point of the two materials.  Finally, the target assembly given in Figure 4.22 was used.  It consists of a normal HOPG graphite target with a small strip of sulphur attached to the graphite target surface.  The sulphur strip was prepared from pure (99.9 %) sulphur powder either by cold pressing or by heating the powder till melting temperature (213 °C) and allowing the resulting melt to resolidify.  The target is mounted on a rotation stage set to rotate at 1 rpm.  Use of such a conceptionally simple approach has also been reported in studies of the co-deposition of metals and DLC; ^{[40],[41] these latter studies demonstrate successful incorporation of the metals as dopants within the DLC film.  The dopant concentration can easily be changed and selected by changing the strip width, which changes the aspect ratio (the relative amounts of the two materials exposed to the laser irradiation), though some preliminary studies are usually needed to establish the respective ablation rates of the two materials.}

Post deposition EDAX analysis of the graphite target showed no significant re-deposition of sulphur on the graphite surface (or C on the sulphur strip), implying that the substrate surface is subjected to either a flow of carbon or sulphur particles, dependent on the position of the laser footprint on the target.

 

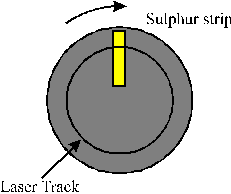
Figure 4.22: Target arrangement used when ablating a C:S target.

 

The pressure in the vacuum chamber was observed to rise from the initial deposition pressure of 5 ´ 10^-6 Torr to much higher values (1 ´ 10^-4 Torr) when depositing C:S films with this target assembly; when ablation stopped the pressure rapidly dropped back to its base value.  Such a pressure rise is much higher than that observed during ablation of graphite and deposition of normal DLC films.  This observation has been investigated further by using the mass spectrometer in Residual Gas Analysis (RGA) mode.  The mass spectrometer was chosen to operate in off-axis alignment (the axis defined by the Mass Spectrometer is at 90° with the surface normal of the target) with the entrance nozzle at a distance of 250 mm to detect gaseous species formed during ablation, with the substrate positioned 5 cm from the target.  The kinetic energy of species detected under these experimental conditions is thermal.  The mass spectrometer was operated with a cage voltage of 3 V and the ioniser voltage was set to 20 V so as to ionise the neutral molecules without fragmenting them by high energy electron impact.  Figure 4.23 shows mass spectra of the residual gas in the chamber (a) when no ablation is occuring and (b) when ablating a C:S target (4 % S aspect ratio).  Both show clear peaks at m/z 18 (H₂O), 28 (N₂) and 44 (CO₂) and look similar except for the additional signal at m/z 76 when ablating C:S targets.  This mass corresponds to CS₂, which is a probable stable, volatile product of C:S ablation.  A small increase of the signal at m/z 34 amu is also noticeable, attributable to H₂S. No peaks were observed at higher masses (m/z > 100 amu).

 

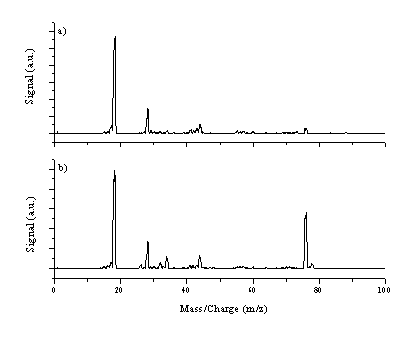
Figure 4.23: Mass spectra of the residual gas (a) no ablation (b) C:S ablation for a laser fluence of 10 J/cm².

Additionally, the time dependence of the relative gas concentration can be studied by continuously monitoring the signal associated with the various m/z ratios.  This was done for two different aspect ratios, namely 4 % S (top trace) and 24% S (lower trace) and a fluence of 10 J/cm².  Figure 4.24 shows that the observed CS₂ signal coincides with the ablation event, particulary with the ablation of graphite.  The signal drops when sulphur is ablated.  The total yield of CS₂ also scales with the aspect ratio.  The absolute scale in Figure 4.24(a) is 1500 counts while that in Figure 4.24(b) is 3500 counts.  The temporal profile of the CS₂ signal drops steeply during the graphite ablation stage in the case of low S:C aspect ratio, but with the higher S:C ratio target this trend is much less noticeable.  The dependence of the water signal during ablation is plotted in Figure 4.24(c).  This shows a long time variation but as expected, is insensitive to whether C or S is being ablated.  The dependence of the 34 amu (H₂S) signal was also studied and gave a temporal dependence similar to, but less explicit than, that of the CS₂ signal.

The dependence of gaseous CS₂ formation during the ablation event can be rationalised as follows.  Since the EDAX measurements indicated that little or no significant re-deposition of sulphur on the graphite target surface and vice versa, production of nascent CS₂ from the target surface as a side product of the ablation process is very unlikely.  Gas phase recombination of the ablation products during flight is also unlikely since, at any one time, essentially pure graphite or pure sulphur will be ablated.  Spikes in the m/z 76 signal observed at the boundary of the graphite and sulphur areas (more noticeable in the 4 % aspect ratio data) might be attributable to co-ablation of carbon and sulphur in a single shot because of the finite size of the laser footprint. 

 

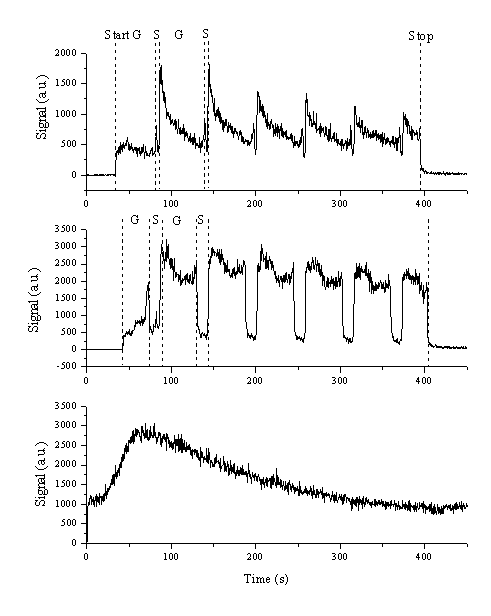
Figure 4.24: Temporal profiles of the m/z 76 signal for S:C aspect ratios of (a) 4 % and (b) 24 %. The dashed lines indicate the different subdivisions of the process; start and stop indicate the beginning and end of the laser ablation process, respectively, and G and S indicate the periods when graphite and sulphur were irradiated by the laser, respectively. (c) shows the temporal profile of the m/z 18 (H₂O) signal during this ablation cycle.

 

The CS₂ gas products are more likely to be generated on the substrate surface and, unavoidably, also on the walls of the ablation chamber, as a by-product of the pulsed laser deposition.  The approach of alternately ablating sulphur and graphite has the major disadvantage that the deposition will result in layered structures.  So, just after tracking the graphite target, the substrate surface will consist of a carbon rich film, and vice versa.  As shown in section 4.7.1, the carbon films deposited under the given experimental conditions are dense DLC films with a high (> 60 %) sp³ fraction.  The surface displacement energy of a sulphur atom (2.88 eV/atom ^[42]) is much lower than for a carbon atom (7.8 eV/atom, ⁴² assumed to be in a graphite lattice) which makes it much more feasible for a sulphur atom to be sputtered by a transient high energy flow of carbon atoms than vice versa.  Sulphur atoms ejected into the gas phase during C atom bombardment will likely recombine to form CS₂.

Films were deposited for 15 minutes using different fluences (5-20 J/cm²) and S:C aspect ratios (7-16 %) and were characterised with Auger spectroscopy and XPS, Raman spectroscopy and SEM.  Compositional results obtained from Auger spectroscopy and XPS analysis are given in Table 4.1.

 

S: C Aspect Ratio	7 %		16 %
Fluence	Auger	XPS	Auger	XPS
5 J/cm2	27	16	46	36
10 J/cm2	11	12	33	25
15 J/cm2	9	10	-	-

Table 4.1: S content (percent) in the deposited C:S films measured by Auger and XPS, the values were deduced from integrating under the peaks attributable to C or S and corrected for the relative sensitivity of the methods to the different species.

 

The techniques show significant differences in the absolute values of the % S within the film, but they show the same trend, namely:

 

(i)                  The percentage of sulphur is dependent on the initial aspect ratio on the target.  This is self-evident, since the more sulphur is ablated, the more sulphur is deposited on the substrate.

(ii)                The amount of carbon in the film scales with the fluence.  This can be explained by the hugely different melting temperatures of both materials, sulphur melts at 486 K ^[43] while carbon melts at 4300 K, which makes graphite a much more difficult material to ablate than sulphur.

(iii)               The total amount of sulphur in the deposited film is always higher than the aspect ratio (by a factor of 1.4-2.8, depending on the fluence), again reflecting the different melting temperatures.

 

The films were also analysed by Raman spectroscopy in an effort to obtain insight into the bonding within the films. Raman spectra of the deposited films are given in Figure 4.25, and Figure 4.26 compares the Raman spectrum of a deposited film with that of sulphur.  The films deposited with lower C:S ratios gave a very small Raman signal, while the Raman spectrum of films deposited with higher C:S ratios were essentially indistinguishable from those of undoped DLC films.  None of the deposited films exhibited features characteristic of elemental sulphur (given in Figure 4.26(a)).

 

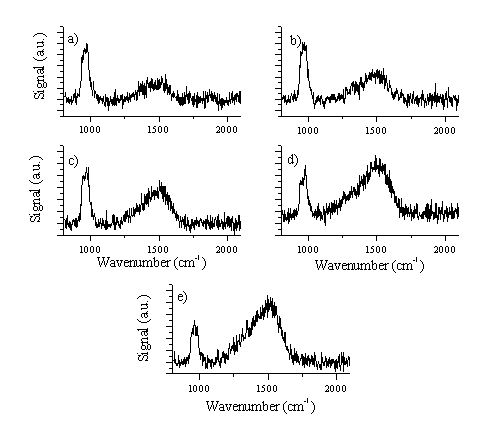
Figure 4.25: Raman spectra of C:S films grown on Si substrate (Si is responsible for the 960 cm^-1 feature), as summarised in Table 4.1, with (a) 16 % aspect ratio / 5 J/cm², (b) 16 % aspect ratio / 10 J/cm², (c) 7 % aspect ratio / 5 J/cm², (d) 7 % aspect ratio / 10 J/cm² and (e) 7 % aspect ratio / 15 J/cm², respectively.

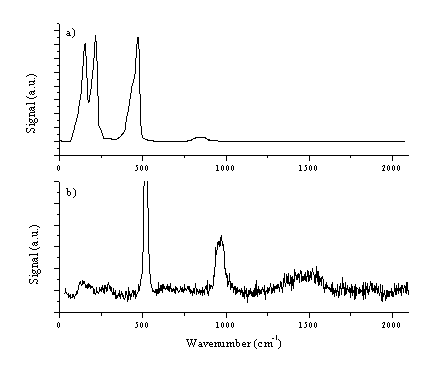
Figure 4.26: (a) Shows a Raman spectrum of sulphur, which can be compared with that of the film with the highest sulphur content (16 % aspect ratio / 5 J/cm²) shown in (b). The 520 cm^-1 feature in (b) is due to the fundamental of the Si substrate.

 

The results can be interpreted as follows.  The films with higher sulphur content exhibit only a small DLC signal.  This could be attributable to the thickness of the film.  Films with a high sulphur content are typically grown with low fluences (5-10 J/cm²) and consequent at low deposition rates.  A second explanation might be that films grown with a high sulphur (40 %) content should no longer be considered as DLC films.  If we assume that the sulphur is incorporated within the DLC lattice, such high doping percentages will create a new material with different structural characteristics.  Films with lower sulphur contents show a Raman spectrum more typical of DLC, comparable to the spectra reported earlier (section 4.7.1).  The absence of strong sulphur features, (compare Figure 4.26(a) and Figure 4.26(b)) indicates that even the S rich films do not contain any extensive S networks.

Closer inspection of the films with SEM shows that the films are smooth but incorporate some needle shaped macroparticles as revealed in Figure 4.27.  These tube-like structures are not observed when growing pure DLC films, but are, to some extent, evident in all the films grown with sulphur doping, indicating a general, sulphur assisted, mechanism for their formation.  However, EDAX mapping of the surface of the film indicates that these structures are not pure sulphur.

 

b)

a)

      

Figure 4.27:  Needle-like structures in the C:S film (16 % aspect ratio / 15 J/cm² /RT) images at high magnification to show the microstructure of the tube-like macroparticles.

 

4.7.4. Conclusions for film deposition

 

193 nm ablation of graphite in vacuum has been studied and shown to lead to DLC films of high quality.  The fluence dependence of the deposition process was the subject of an earlier study; the quality, as determined by laser Raman spectrometry, of the produced films remains constant throughout the fluence region.²⁸ 

The 193 nm PLA of both CVD diamond and graphite samples, in vacuum, have been compared and contrasted - both from the perspective of the ablation plume and by investigation of the resulting DLC films deposited on Si(100).  The composition and propagation of the plumes from both targets have been probed via wavelength, spatially and temporally resolved studies of the plume emission and by Langmuir probe TOF methods and found to be very similar, thereby extending and conforming results reported in a previous study.²⁸

The deposited DLC films grown on Si substrates maintained at room temperature were studied by laser Raman spectroscopy, by both optical and scanning electron microscopy, and their field emission characteristics investigated.  Again, similarities outweigh the differences, but DLC films grown from ablation of the diamond target appear to show steeper I/V dependencies once above the threshold voltage (~ 50 V/mm) for field emission. 

The results of the sulphur doping study show that it is possible to deposit sulphur containing DLC films with percentages ranging from 10 to 40 % sulphur.  The observed pressure rise during deposition indicated a gas formation mechanism, which we attribute to CS₂ formation as a result of reactive sputtering of previously deposited sulphur from the surface of the substrate and the vacuum chamber walls.  Interestingly, CS₂ formation is also observed in the CVD of sulphur containing diamond films from CS₂/H₂ + CH₄/H₂S/H₂ gas mixtures, as shown by our laboratory. ^[44]

The Raman spectra of the sulphur doped films showed the characteristic DLC feature in the case of films grown with low sulphur concentrations, but this feature becomes less pronounced in the case of films grown with higher sulphur content.  The surface of the films appears smooth, but some needle-shaped macroparticles are embedded.  These macroparticles appear to be a characteristic feature of films formed by co-deposition of carbon and sulphur.

 

4.8. References