5. Results for C/H/O Systems

 

5.1. Introduction

 

This chapter presents the results of MWCVD diamond growth experiments using 50%CH₄/50%CO₂ gas mixtures and various substrate temperatures, T_sub.  MBMS and OES experimental measurements and SENKIN computer simulations of CH₄/CO₂ plasma species are also presented over a range of CH₄:CO₂ mixing ratios.  Computer simulations have been extended to include 37 further binary H/C/O gas mixtures, thus allowing prediction of the boundaries of the diamond CVD atomic phase (Bachmann) diagram (see Section 1.14.1).  In this chapter CH₄/CO₂ gas mixtures will be defined in terms of %CH₄, i.e. %CH₄ = 100-%CO₂.

 

5.2. Low Temperature Diamond Deposition From 50%CH₄/50%CO₂ Gas Mixtures

 

MPCVD experiments were undertaken in which films were deposited using 50%CH₄/50%CO₂ gas mixtures with applied microwave power of 1 kW and pressure of 40 Torr.  Growth was carried out for a range of T_sub controlled independently by a cooled substrate holder (Section 3.2.3).  Diamond films were analysed by SEM and LRS, as discussed below.

 

5.2.1. Film Crystalinity

 

Deposited films were analysed by SEM in order to investigate the effect of T_sub, on deposited film crystallinity and facet size.  Electron micrographs of four such films are presented in Figure 5.1.

 

Figure 5.1. Electron micrographs of films deposited from 50%CH₄/50%CO₂ plasmas.  Conditions:  1 kW applied microwave power, total gas flow 80 sccm, pressure 40 Torr, growth time 8 h.  Substrate temperature: (a) 435°C; (b) 590°C; (c) 650°C; (d) 845°C.  Cross-sections of two of these films are given in (e) 435°C and (f) 845°C.

 

At 435°C (a) the deposit is made up of a barely continuous film of smooth rounded particles.  A second layer of isolated rounded particles is beginning to form on top of the first layer, but appears to be poorly adhered.  At these low temperatures the temperature difference between the top of the film (closer to the hot plasma) and the bottom of the film (in contact with the cooled substrate) may be sufficient to cause a significant difference in growth rates in the two regions.  Thus deposition occurs faster on top of existing structures, and the deposit grows as rounded isolated pillars.  This can clearly be seen in the cross-section (e), where pillars made from rounded crystallites rise above a smooth continuous coating.  At 590°C (b) and 650°C (c) a continuous film is obtained, but with poorly defined crystal facets and small crystal size.  The crystallinity improves with increasing substrate temperature, while the number of grain boundaries decreases producing larger crystallites.  At 845°C (d) a continuous film with well-defined, (111) crystalline facets is obtained.  The cross-section of this film (f) now shows the familiar columnar growth which is characteristic of normal CVD diamond.

 

5.2.2. Film Growth rate

 

Deposited film growth rate was investigated by measuring film cross-sectional thickness from SEM (Section 2.2).  Film growth rate is seen to decrease as the substrate temperature falls (see Figure 5.2).  At a substrate temperature of 500°C the growth rate is only 0.1 mm h^‑1. 

 

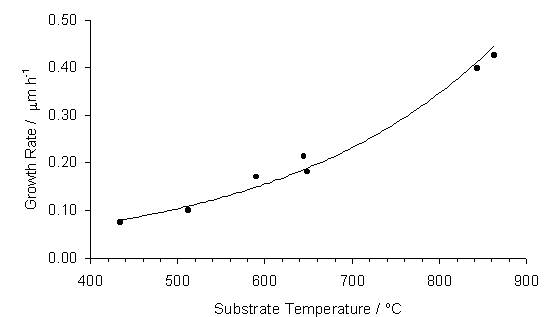
Figure 5.2. Film growth rate (measured by cross-sectional SEM) versus substrate temperature for films grown in 50%CO₂/50%CH₄ plasmas.  The line is a least squares fit to an exponential function.

 

An Arrhenius plot for the growth rate data is displayed in Figure 5.3.  A least squares fit to the data yields a gradient from which an overall activation energy for film deposition of 28 ±1.6 kJ mol^-1 can be calculated.  These growth rate data fit well with the trend obtained by plotting a number of different CVD diamond growth experimental rates, as published by Corat et al [[1]] (see Section 1.12)

 

However, this activation energy is much lower than the value of 97 kJ mol^-1 obtained by Kondoh et al [[2]] using a similar analysis of film growth rates obtained using a hot filament CVD reactor and CH₄/H₂ process gas mixtures.  In both that report, and the work presented here, the film growth rate was calculated by measuring film thickness by cross-sectional SEM and dividing by the total growth time.  However, Snail and Marks [[3]] have pointed out that there is likely to be an (undetermined) nucleation period prior to film growth, and that calculations of activation energy based on such growth rates thus have an inherent uncertainty.  Maeda et al. [[4]] circumvented the problem of an undetermined incubation period by studying changes in the shape of crystals with continued diamond growth (using a 1%CH₄/H₂ microwave plasma) and obtained activation energies of 31 and 84 kJ mol^-1 for the (100) and (111) crystal planes, respectively.  The lower activation energy for CO₂/CH₄ presented here, compared with values from H₂/CH₄ gas mixtures, hints at different fundamental growth steps for these two gas mixtures.  It also provides a clue as to why these CO₂/CH₄ plasmas are able to deposit diamond at lower temperatures.

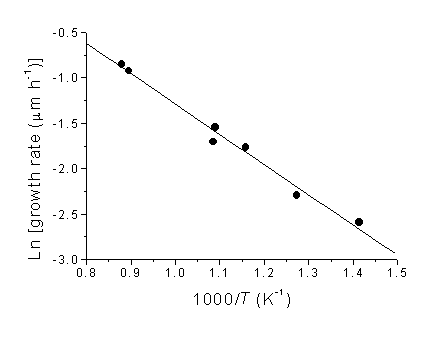
Figure 5.3. Arrhenius plot of ln(film growth rate) versus inverse substrate temperature, 1/T.  The gradient of the fitted line gives an overall activation energy for film deposition of 28 ±1.6 kJ mol^-1.

 

5.2.3. LRS Analysis of Films

 

Figure 5.4 demonstrates that with decreasing deposition temperature, the full-width half-maximum (FWHM) of the diamond laser Raman peak at 1332 cm^-1 increases, indicating a decrease in the quality of diamond.  The height of the diamond peak relative to the graphitic G-band at ~1550 cm^-1 also decreases with decreasing temperature, reflecting an increase in sp²-bonded carbon content in the films.  Since the substrate temperature was controlled independently from other process parameters, the observed decrease in crystallinity, quality and growth rate with lowered substrate temperature is likely to be due to the reduced efficiency of gas-surface and/or surface reaction(s).

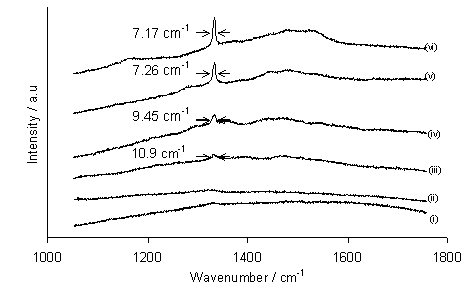
Figure 5.4. Laser Raman spectra (514.5 nm excitation) of films grown in a 50%CO₂/50%CH₄ mixture at substrate temperatures of: (i) 435°C; (ii) 512°C; (iii) 590°C; (iv) 650°C; (v) 845°C; (vi) 865°C.  Conditions: as given in Fig. 5.1.  The FWHM values (as estimated from spectra) for the diamond peak at 1332 cm^‑1 are shown on each plot.  The spectra have been offset vertically for clarity.

 

5.3. OES Studies of CH₄/CO₂ Microwave Plasmas

 

Figure 5.5 illustrates the change in visual appearance of the plasma for differing CH₄/CO₂ compositions.  100% CO₂ plasmas (Fig.5.5(a)) appear deep blue with a white centre.  With additions of <55%CH₄ (Fig.5.5(b)), the plasma does not change significantly in appearance, except that its colour becomes a lighter blue.  Above 55%CH₄ an orange halo begins to form at the edges of the plasma ball, and the central plasma becomes blue-yellow (Fig.5.5(c)).  Just above the substrate there is a small region ~1 mm wide where the plasma appears violet.  The orange halo is believed to be a result of black body emission from soot particles that have coalesced in the cooler regions of the plasma [[5]]. 

 

Figure 5.5. The visual appearance of CH₄/CO₂ plasmas with methane contents of (a) 0 (i.e. 100%CO₂), (b) 50%, (c) 70% and (d) 100%.

 

With further increases in %CH₄ the orange halo increases in size and brightness, accompanied by rapid deposition of soot on the chamber walls.  100% CH₄ plasmas (Fig.5.5(d)) have a bright white centre with an extensive orange halo.  Excessive soot deposition at high %CH₄ prevented detailed measurements at these compositions; the MBMS results thus do not extend beyond 80%CH₄.

 

Figure 5.6 shows OES spectra for three different gas compositions.  The spectrum of a 20%CH₄/80%CO₂ microwave plasma (Fig.5.6(a)) is dominated by intense OH (A-X) emission around 308 nm, but other emissions due to CO, OH and H_b can also be seen clearly.  Figure 5.6(b) shows the OES spectrum for a 50%CH₄/50%CO₂ plasma, the optimal gas mixture for growth of good quality diamond [5].  Emission from OH (282 and 308 nm) is now dramatically reduced in intensity, and no longer obscures the 3^rd Positive and 5B bands (260-370 nm) of CO.  Emissions due to C₂ (Swan band 460‑480 nm and 500-515 nm) and CH (431 nm) are also seen.  A broad emission feature centred at ~400 nm is due to C₃ radicals.  The OES spectrum from an 80%CH₄/20%CO₂ plasma (Fig.5.6(c)) is dominated by C₂ emission, whilst CO and CH emissions are now smaller relative to the increased C₃ feature.

 

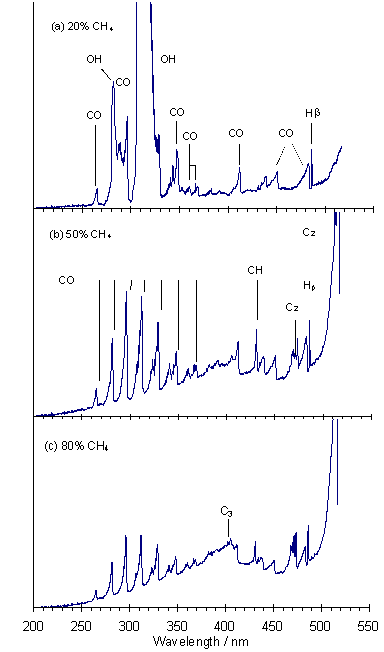
Figure 5.6. (a) OES spectra of plasmas involving (a) 20%CH₄/80%CO₂, (b) 50%CH₄/50%CO₂, and (c) 80%CH₄/20%CO₂, other conditions as given in Fig.5.1.  Note: the response of the CCD detector was more sensitive to longer wavelengths.

 

5.4. Molecular Beam Mass Spectrometry studies of CH₄/CO₂ Microwave Plasmas

 

All MBMS measurements were made under the same conditions as the deposition runs, except that the gas mixing ratio was varied and the applied microwave power was increased to 1.2 kW.  This is because the presence of the sampling probe reduced the stability of the plasma at 40 Torr, making a higher applied power necessary in order to maintain a stable plasma at this pressure.  Table 5.1 is a key for symbols used in Figure 5.7.  Identical symbols are also used in the plots of SENKIN predicted mole fractions in Section 5.5.

 

Table 5.1. Key of species symbols used in Figures 5.7 to 5.11

 

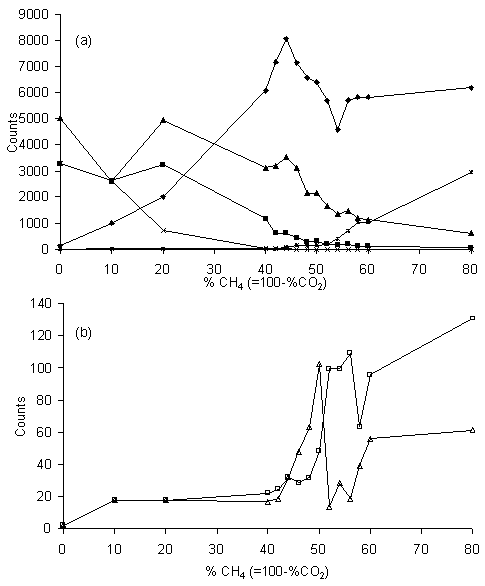
Figure 5.7 MBMS plots of species counts versus %CH₄ in a CO₂/CH₄ gas mixture.  The data for H₂ have been reduced by a factor of 40 to fit onto the vertical scale.  Conditions as given in Fig.5.1, except applied microwave power increased to 1.2 kW to improve plasma stability.

 

Figure 5.7 shows the MBMS counts measured for (a) CO₂, CO, H₂O, H₂ and C₂H₂ and (b) CH₃ and CH₄, versus the plasma composition.  Here it is worth re-emphasising that the relative sensitivity of the mass spectrometer to each species is unknown, and that the relative trends of each species are the feature of particular interest.  Looking at the trends of each species in turn (with gas mixtures quoted as %CH₄):

·        CO₂: the CO₂ counts fall from an initial high value at 0% CH₄ to zero at 40% CH₄.  This result shows that, even though CO₂ is one of the original input gases, for gas compositions containing more than 40% CH₄ all of this CO₂ is destroyed and converted to other products.

·        CO and H₂O:  these follow similar trends, both rising to a peak at ~20% CH₄, before falling off steadily with further increases in %CH₄.

·        C₂H₂: acetylene counts only appear above the background noise for gas mixtures containing over 50% CH₄, but thereafter increase steadily.

·        H₂: the counts for hydrogen rise with increased %CH₄, before levelling out after about 60% CH₄.  However, measurements of this low mass species must be treated with some caution given the large scatter in experimental data.

·        CH₃ and CH₄: counts for CH₃ and CH₄ remain at background levels for low %CH₄ input, and only reach detectable levels above 40% CH₄.  This means that for low %CH₄ gas mixtures most, if not all, of the input CH₄ gas is being consumed and converted into other products.  At higher %CH₄ mixtures, the curves for both CH₄ and CH₃ rise rapidly to a peak, then fall again over a composition range in which the %CH₄ varies by only ~5%, and thereafter continue rising.  The position of the peak is slightly different for the two species: for CH₄ and CH₃ it occurs at 56% and 50% CH₄, respectively.  Note that the peak in CH₃ counts coincides very closely with the gas mixture at which the optimum diamond film growth rate and quality is obtained [5,[6]].  Note also that the counts of CH₃ and CH₄ are, in general, an order of magnitude lower than those of the other species measured.

·        Higher hydrocarbons: Counts for C₂H₆ or higher hydrocarbons (e.g. C₃, C₄ species, etc.), were not detected, even at very high %CH₄.  This is somewhat surprising, given the high levels of soot deposition seen in high %CH₄ plasmas and may, in part at least, be the result of dissociative ionisation of the higher hydrocarbons by the 18 eV electrons within the source region of the mass spectrometer.  OES and visual inspection (Fig.5.5) suggests that soot formation occurs at the periphery of the plasma, where the gases are cooler.  Thus, another explanation may be that no higher hydrocarbons are present in the hotter central region of the plasma, from where the gas is sampled.

·        O, O₂ and OH: counts for these reactive oxygen-containing species are also absent, and it appears that all the oxygen is ‘locked-up’ within stable molecules, such as H₂O, CO₂ and especially CO.  That the concentrations of these reactive species are all below our detection limit encourages the view that they do not play a significant role in the gas phase or surface chemistries, and are therefore not directly involved in the rate limiting processes leading to low temperature diamond growth, contrary to previous suggestions [[7],[8]].

 

5.5. Conditions for Computer Simulations of CH₄/CO₂ Gas Mixtures

 

A number of SENKIN simulations were carried out in order to determine which conditions gave the best agreement to MBMS experimental species trends.  The effect of simulation time and temperature were investigated, as discussed below.  Thus, the reaction time and temperature conditions for SENKIN calculations were decided as 5 s and 2000 K, respectively.  The key for all plots of SENKIN predicted mole fractions, X, contained in this section is as given in Table 5.1 in Section 5.4. 

 

5.5.1. Computer Simulation Time

 

Figure 5.8 shows plots of X vs simulation time for a 50%CH₄/50%CO₂ gas mixture.  SENKIN mole fractions of (a) CO₂, H₂O and C₂H₂ and (b) CH₃ and CH₄ are all seen to fall steeply as simulation time is increased from 1 to 10 s, before leveling out by time = 20 s.  Plots of X vs %CH₄ (for CH₄/CO₂ gas mixtures) for various simulation times are given in Figure 5.9.  A time of 0.01 s (Fig.5.9(a)) results in plots of H₂, CO, CO₂, H₂O C₂H₂, CH₄ and CH₃ species mole fraction trends that do not correlate with those observed for measured MBMS species counts (Fig.5.7).  Increasing the simulation time to 0.1 s (Fig.5.9(b)) improves the agreement between SENKIN and MBMS species trends, although significant mole fractions of CH₄ are predicted by SENKIN for %CH₄ <50% (Fig.5.9(b)(ii)), in disagreement with CH₄ MBMS species count trends seen in Figure 5.7. 

 

Much better agreement is seen for a simulation time of 1 s.  H₂ predicted mole fractions, [H₂], are seen to increase with increased %CH₄, while [CO₂] decreases until no CO₂ is seen for %CH₄ >50%.  [CO] rises, reaches a peak at ~30%CH₄, before falling as %CH₄ is increased.  A similar trend is seen for [H₂O] except no H₂O is seen for %CH₄ >50%.  No C₂H₂ is predicted for %CH₄ <50% although [C₂H₂] rises steadily at higher %CH₄.  The predicted trend in CH₄ (Fig.5.9(c)(ii)) still disagrees with that seen for MBMS measured species counts, in that SENKIN predicts [CH₄] rising from >45%CH₄.  A simulation time of 5 s yields a plot in which a peak in [CH₄] is predicted at 50%CH₄ (Fig.5.9(d)(ii)), in agreement with the measured MBMS CH₄ count trend.  Other species mole fractions (Fig.5.9(d)(i)) are seen to be very similar to those predicted for a reaction time of 1 s (Fig.5.9(c)(i)).  The peaks in [CH₄] and [CH₃] at 50% CH₄ are no longer present for a plot produced using a simulation time of 20 s (Fig.5.9(e)(ii)).  However, the use of this time results in little change in the trends of other species X (Fig.5.9(e)(i)), compared with 1 and 5 s.  This reflects the levelling off in species X seen in Figure 5.8 for simulation times >5 s.  It was concluded that (for a temperature of 2000 K) a simulation time of 5 s gave the best overall agreement between trends in calculated species X and measured MBMS species counts.

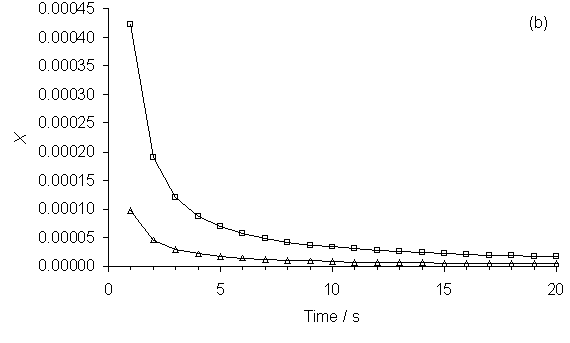
Figure 5.8. Plots of SENKIN simulated species mole fractions, X, vs simulation time for (a) CO₂, H₂O and C₂H₂ and (b) CH₃ and CH₄.  Conditions: gas mixture 50%CH₄/50%CO₂, pressure 40 Torr, temperature 2000 K.  Key: see Table 5.1.

 

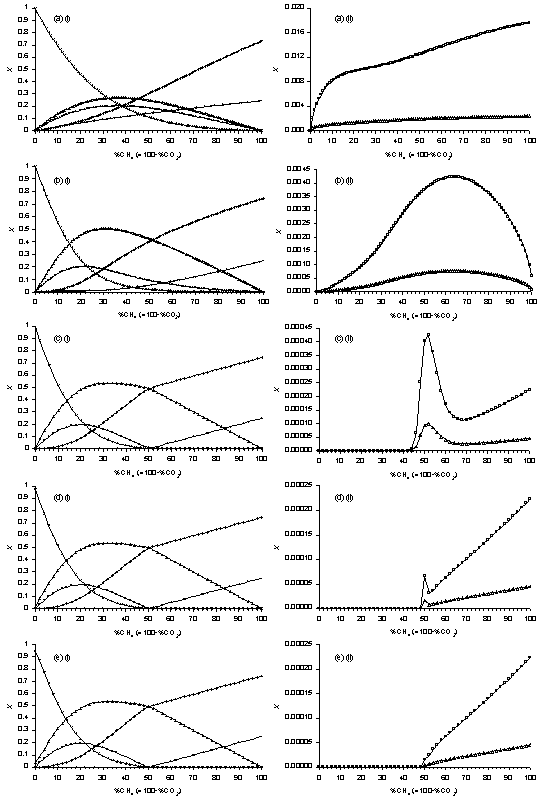
Figure 5.9. Plots of SENKIN simulated species mole fractions, X, vs %CH₄ in CH₄/CO₂ mixtures.  Conditions: pressure 40 Torr, temperature 2000 K, simulation time (a) 0.01 s, (b) 0.1 s, (c) 1 s, (d) 5 s, (e) 20 s.  Key: see Table 5.1.

5.5.2. Computer Simulation Temperature

 

Figure 5.10 is a plot of species X versus temperature for a 50%CH₄/50%CO₂ gas mixture.  CH₄ and CO₂ are seen to undergo reaction at temperatures >1200 K forming H₂, CO, H₂O and C₂H₂.  [H₂] and [CO] increase with rising temperature until these species comprise the majority of the gas mixture at temperatures >1800 K.  [H₂O] and [C₂H₂] both reach peaks at a temperature of 1525 K, after which both decline with increased temperature.

 

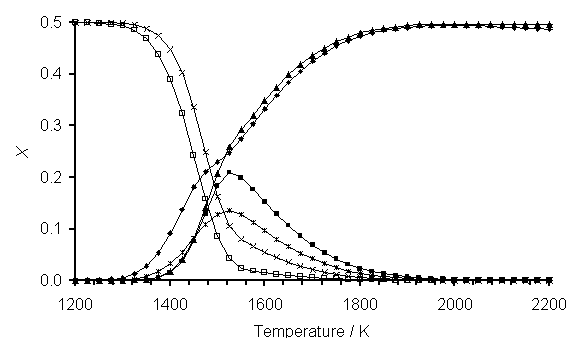
Figure 5.10. Plot of SENKIN simulated species mole fractions, X, vs simulation temperature for H₂, CO₂, CO, H₂O, CH₄ and C₂H₂.  Conditions: gas mixture 50%CH₄/50%CO₂, pressure 40 Torr.  Key: see Table 5.1.

 

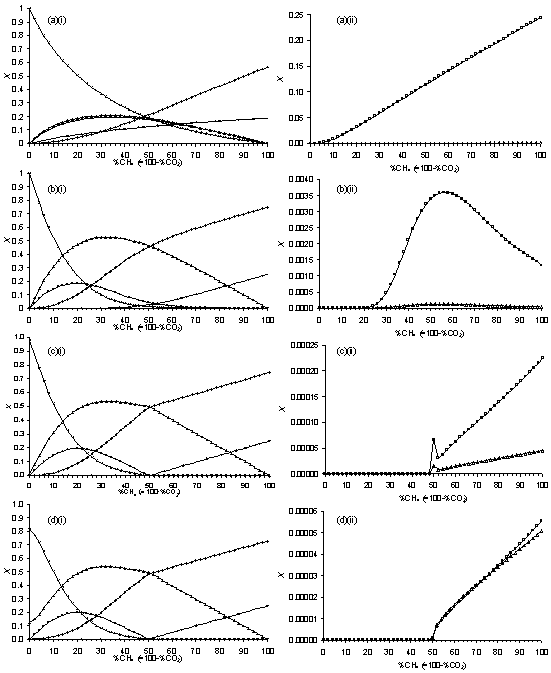
Figure 5.11. Plots of SENKIN simulated species mole fractions, X, vs %CH₄ in CH₄/CO₂ mixtures.  Conditions: pressure 40 Torr, simulation time 5 s, temperature (a) 1500 K, (b) 1750 K, (c) 2000 K, (d) 2250 K.  Key: see Table 5.1.

 

Figure 5.11 shows that (for a simulation time of  5 s) a temperature of (a) 1500 K produces species X with trends which do not agree well with those observed for corresponding MBMS measured species counts (Fig.5.7).  Better agreement is obtained using a temperature of 1750 K (Fig.5.11(b)), although the peak in CH₄ MBMS measured counts is much narrower than that simulated.  Figures 5.11(c)(i) and (ii) shows that a temperature of 2000 K gives very good agreement with MBMS species count trends (as for the identical plots Fig.5.9(d)(i) and (ii), discussed above).  Increasing the simulation temperature from 2000 K to 2250 K has little effect on the trends in X observed for H₂, CO₂, CO, H₂O and C₂H₂.  However, the peaks in both [CH₃] and [CH₄] at 50%CH₄ are both now absent.  This temperature is also in good agreement with that measured previously for a 50%CH₄/50%CO₂ microwave plasma operating under similar conditions [5].

 

5.6. Computer simulation results and comparison with experiment for CH₄/CO₂ Gas Mixtures

 

Figure 5.12 displays combined plots of SENKIN calculated species X and MBMS measured species counts versus plasma composition (%CH₄).  The experimental and calculated plots have been scaled vertically to emphasise the remarkable degree of agreement between the two.  The falling trend in measured CO₂ counts, and the absence of detectable CO₂ for gas mixtures >45% CH₄ (Fig.5.12(i)) are both reproduced by SENKIN simulations.  The trends in calculated CO and H₂O mole fractions (Figs.5.12(ii) and (iii)) are also similar to those observed although rather higher counts of CO and H₂O are seen in experiment at 100% CO₂, where the simulation predicts zero mole fractions for both species.  The presence of CO in the experimental chamber, which is not predicted by the simulation (when using a temperature of 2000 K), may be a result of increased thermal dissociation of CO₂ (to form O and CO) which is found when increased temperatures are used in the simulation.  This suggests that the temperature of a pure CO₂ plasma is higher than that for a CO₂/CH₄ plasma (consistent with the increased substrate temperature measured when using a pure CO₂ plasma).  This increased temperature for 100% CO₂ might also contribute to the unexpected presence of H₂O counts, by promoting desorption from the chamber walls.

 

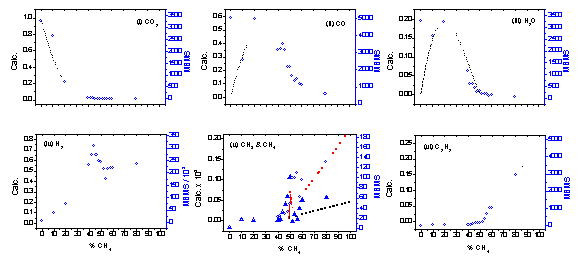Figure 5.12. MBMS plots of species counts (right hand scale) and SENKIN calculated mole fractions (left hand scale) versus %CH₄, in a CO₂/CH₄ gas mixture, for the following species: (i) CO₂, (ii) CO, (iii) H₂O, (iv) H₂, (v) CH₃ and CH₄,  (vi) C₂H₂.  MBMS results are as given in Fig.5.1, except applied microwave power was increased to 1.2 kW to improve plasma stability.  SENKIN computer simulation results are for a CO₂/CH₄ gas mixture at a temperature of 2000 K and a pressure of 40 Torr.  Key: о MBMS species counts, (·) SENKIN computer simulation mole fractions, except (v): ▼ MBMS CH₃ counts, (│││││ ) calculated CH₃ mole fractions, о MBMS CH₄ counts, (·) calculated CH₄ mole fractions.

 

The observed trend in C₂H₂ counts (i.e. a steady rise from zero at ~50% CH₄ gas mixture, Fig.5.12(vi)) is also reproduced well by simulation, as are the experimental data for H₂ (Fig.5.12(iv)).  The shape of the curves, trends, and peaks in CH₃ and CH₄ counts are also reproduced well (Fig.5.12(v)), although the position of the peak in CH₄ counts is shifted by ~5% between the observed and simulated results.

 

The simulation also predicts very low mole fractions (< 10^-6) for O, OH, O₂ and C₂H₆ (for gas compositions around 50% CH₄, in agreement with the lack of measured counts for these species.  The ability of CO₂/CH₄ gas mixtures to enable diamond growth at reduced substrate temperatures (compared to H₂/CH₄ chemistries) is therefore unlikely to be directly due to the presence of O, O₂ or OH in the plasma.  Conversely the high levels of CO present in the plasma, found both in experiment and simulation, suggests that CO may be important to the gas-surface chemistry, and therefore to the ability of CO₂/CH₄ gas mixtures to facilitate low temperature growth of diamond.

It is of note that the very good agreement between experiment and simulation for these gas mixtures (especially over the range of plasma compositions used for diamond deposition, 45-55% CH₄) arises without including electron impact dissociation or any ionic reactions.  Such a finding serves to reinforce previous suggestions [[9]] that these reactions do not constitute a significant part of the plasma chemistry in typical low‑pressure MWCVD reactors.

 

5.7. Discussion of Results For CH₄/CO₂ Gas Mixtures

 

5.7.1. Termination of Diamond Growth Surface

 

Comparing growth rate data at different substrate temperatures for CH₄/H₂ and CH₄/CO₂ gas mixtures, some insight into the growth mechanisms can be deduced.  Creation of a dangling bond by abstraction of a hydrogen atom from the diamond surface by reactive gas phase H atoms is generally considered to be a key part of the rate limiting step in the growth mechanism from H₂/CH₄ gas mixtures [15].  The activation energy for diamond growth using 1%CH₄/H₂ gas mixtures has been measured by Kondoh et al [2] as 97 kJ mol^-1 and by Maeda et al. [4] as 31 and 84 kJ mol^-1 for the (100) and (111) crystal planes, respectively.  In the present work, Figure 5.3 suggests an activation energy for CH₄/CO₂ plasmas of only 28 kJ mol^-1.  This much lower value suggests that there may be fundamental differences in the rate limiting growth step for diamond CVD using these two gas systems, although the work of Corat et al [1] (as discussed in Section 1.12) does cast some doubt over this conclusion.

 

Table 5.2 shows that under optimal growth conditions (50% CH₄), species such as O, O₂ and OH are present in amounts that are too small to account for a significant change in growth chemistry.  We note that the gas phase concentration of CO predicted to be present within the CO₂/CH₄ plasma is ~100 times that of atomic H (see Table 5.2).  Thus, even if the lower activation energy argument given above is discounted, CO must be considered as an alternative species that could terminate the growing diamond surface. 

 

Table 5.2.  Species mole fraction results from SENKIN simulations of 1% CH₄/H₂ and 50% CO₂/50% CO₂ gas mixtures.  Conditions: temperature 2000 K, pressure 40 Torr.

 

Although a CO-terminated structure is possible, since it involves an unpaired electron it is likely to be rather unstable, and the CO would be expected to readily desorb.  A more stable surface termination would occur if the terminating species were CHO (formyl radical), as shown in Figure 5.13.  This could be formed by direct addition of an H (with the excess energy dissipated within the lattice) or by abstracting a neighbouring surface terminating H atom.  This latter process is attractive in that it provides a means by which the ‘dangling bond’ can migrate across the growing diamond surface (e.g. to a step edge).

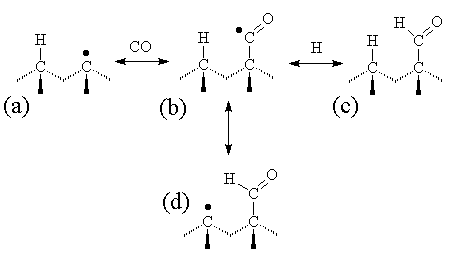
Figure 5.13. A model for the behaviour of CO on a diamond surface.  (a) a reactive site on the diamond surface (the unpaired electron indicated by a dot) reacts with a gas phase CO molecule to form an unstable carbonyl radical adduct, (b).  This adduct will most likely rapidly desorb back to (a), although another possibility is that it can be temporarily stabilised by addition of H to form an aldehyde.  The H atom could be from the gas phase (c), or a terminating H atom from a neighbouring surface site (d).

 

We can obtain insight into the thermodynamics of such systems by approximating the structure of the CHO and H-terminated diamond surfaces as tertiary butyl fragments bonded to either CHO or H leaving groups.  Thus, we wish to compare the (CH₃)₃C‑H bond energy of tertiary butane with the (CH₃)₃C‑CHO bond energy of 2,2-dimethylpropanal.  The bond energy of the former is known from standard tables [[10]] to be –390 kJ mol^-1.  The relevant C-C bond energy for the latter can be estimated by summing the enthalpies of formation of its component parts, following the method given in Reference [11].  This calculation gives a value for the standard enthalpy of formation of gaseous (CH₃)₃CCHO of ~ ‑244 kJ mol^‑1, which compares favourably with the known enthalpies for similar molecules, such as n‑pentanal (‑228.5 kJ mol^‑1) and butan-2-one (‑262.5 kJ mol^‑1).  Since the standard enthalpies of formation of the (CH₃)₃C and CHO radicals are known [10] to be +37.8 kJ mol^‑1 each, then Hess’s law gives an estimate for the relevant C-C bond energy in (CH₃)₃C‑CHO as –320 kJ mol^-1, some 70 kJ mol^-1 weaker than the H-terminated structure.  Thus we envisage a more dynamic surface chemistry than with the traditional CH₄/H₂ gas mixtures, involving frequent attachment and detachment of CO molecules to and from the surface, some stabilisation of these CO molecules as HCO adducts, and enhanced opportunity for site migration even at low substrate temperatures.

Itoh and Matsumoto [[12]] used X-ray photoelectron spectroscopy to identify adsorbed CO molecules on the surface of deposits obtained from a CO₂/CH₄ microwave plasma.  They went on to speculate that CO may be a growth species when using such gas mixtures.  However, Eaton and Sunkara [[13]] concluded that although CO species are dominant in the gas phase chemistry they do not participate in gas-surface chemistry.  Such contradictions highlight the lack of knowledge of gas-surface chemistry occurring during CVD growth using CO₂/CH₄ gas mixtures.

 

5.7.2. Diamond Growth Species

 

We turn now to the question of the growth species.  In CH₄/H₂ gas mixtures, the growth species are believed to be methyl radicals, which react with dangling bonds on the surface, so adding a carbon to the lattice.  In CH₄/CO₂ mixtures, the peak in CH₃ observed both in experiment and simulation coincides very precisely with the narrow window for optimum diamond deposition (50%CO₂/50%CH₄).  The fact that there is no similar maximum in the concentration of CO (nor any other species) around this narrow concentration window, provides strong evidence that CH₃ is the species responsible for diamond growth, rather than CO or C₂H₂.

 

5.7.3. Gas-Phase CH₄/CO₂ Plasma Chemistry

 

The trends observed in the measured counts of CO₂, CO and H₂ (i.e. with increasing %CH₄ the CO₂ counts fall while CO and H₂ counts rise) can be explained in terms of the overall reaction scheme 5.1.  Note that this ‘overall’ reaction is actually the net result of a sequence of 12 elementary reactions involving atoms, radicals and molecular fragments.

 

CO₂ + CH₄  ¾  2CO + 2H₂                            Reaction 5.1

2CH₄  ¾  C₂H₂ + 3H₂                                     Reaction 5.2

 

The values for the enthalpy, DH, the entropy, DS, and the Gibbs free energy, DG, for Reaction 5.1 at 2000 K are 251, 0.279 and ‑306 kJ mol^-1, respectively [[14]].  The high negative value for DG shows that this reaction occurs spontaneously at these temperatures and that the equilibrium lies far to the right hand side (with equilibrium constant, K_eq ~ 10⁸, obtained using the relationship DG = -RTlnK).  Note that there is a 1:1 stoichiometric relationship between the two reactants, CO₂ and CH₄.  This means that each CO₂ molecule will react with and ‘destroy’ a CH₄ molecule, but as soon as there is an excess of either of the reactants, that reactant will then be able to undergo further reactions.  Therefore at compositions < 50% CH₄, Reaction 5.1 is responsible for the destruction of all CH₄ and therefore the suppression of C₂H₂ formation via overall Reaction 5.2.  The excess CO₂ is converted into CO and water.  Above 50%CH₄ there is now an excess of CH₄, so that not all CH₄ is destroyed in Reaction 5.1.  Unreacted CH₄ is thus available to react to form C₂H₂ (reaction 2), thus explaining why C₂H₂ is only observed at compositions >50%CH₄.  Such trends, and their sensitivity to the relative partial pressures of CH₄ and CO₂, reinforce the general discussion of diamond CVD using H/C/O gas mixtures as reviewed by Goodwin and Butler [[15]].

 

The observed trend in measured counts of H₂O (i.e. peaking at 20% CH₄ before falling to zero at 50% CH₄) can be explained by overall Reaction 5.3.  The values of DH, DS and DG for this reaction at 2000 K are 26, 0.026 and –25 kJ mol^-1, respectively [14].  Again, the negative value of DG shows that this reaction occurs spontaneously at these temperatures and that the equilibrium favours the products (K_eq = 5).  Thus, this reaction serves to reinforce Reaction 5.1, reducing CO₂ to CO with concomitant conversion of H₂ to water.

 

CO₂ + H₂ ¾ CO + H₂O                                  Reaction 5.3

 

The local peak in CH₄ concentration at 50%CO₂/50%CH₄, seen both experimentally and in simulation, coincides with the composition where the product of the C₂H₂ and H₂O concentrations is a maximum (see Figure 5.14).  This suggests that this peak in CH₄ concentration is due to an overall reaction between C₂H₂ and H₂O, such as reaction 5.4.

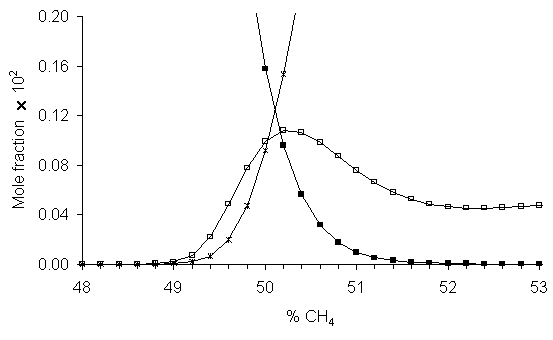
Figure 5.14. Calculated species mole fractions close to the 50%CH₄ region, showing H₂O concentrations falling and C₂H₂ concentrations increasing.  The species concentrations are equal at approximately the position where CH₄ concentration peaks.  The data for CH₄ have been multiplied by a factor of 15 to fit onto the vertical scale.  Key: ■ H₂O, Þ C₂H₂, □ CH₄.

 

H₂O + C₂H₂  ¾  CH₄ + CO                            Reaction 5.4

 

The values for DH, DS and DG for this reaction at 2000 K are ‑180, ‑0.022 and ‑137 kJ mol^-1, respectively [14].  DG is again large and negative, showing that this reaction occurs spontaneously at these temperatures, and that the equilibrium lies well over to the right hand side (K_eq = 3700).  At higher %CH₄, the CH₄ concentration is in equilibrium with that of C₂H₂ via reaction 2.  The peak in CH₄ (and also CH₃) concentration around 50% CH₄ can now be seen as the result of competition between two reactions, which begin to contribute and to oppose each other as soon as there is more CH₄ than CO₂.  With increasing %CH₄, there is less CO₂ present in the plasma, and as this is a reactant in Reaction 5.3, less product (H₂O) is formed.  Thus, the concentration of H₂O falls.  But at the same time, increasing %CH₄ increases the amount of C₂H₂ present (Reaction 5.2).  So, in reaction 5.4, as the % CH₄ is increased one reactant (H₂O) is decreasing in concentration whilst the other (C₂H₂) is increasing.  The concentration where the 1:1 stoichiometry occurs for maximum yield (i.e. maximum CH₄ product) is where the two curves cross, at 50-51%CH₄.  This small window where the CH₃ concentration is maximized, with minimal C₂H₂ present, is the diamond growth window.  At even higher CH₄% there is more total CH₃ present, but this is swamped by the excess of C₂H₂, with the result that, as in the traditional CH₄/H₂ chemistry, the deposited films become increasingly graphitic in nature.

 

5.8. Modelling of the C-H-O Diamond CVD Atomic Phase Diagram

 

Calculations were carried out for 38 gas mixtures, exploring the full composition range in each case (e.g. 100% CH₄ to 100% H₂ for a CH₄/H₂ mixture).  All combinations of each of the hydrocarbons CH₄, C₂H₂, C₂H₃, C₂H₄, C₂H₅ and C₂H₆, with each of the species CO, CO₂, O₂, H₂O, OH and HO₂ were considered, as well as CH₄/H₂ and C₂H₂/H₂ mixtures.  Figure 5.15 shows the calculated variation in the mole fractions of H atoms, CH₃ radicals, and H₂, C₂H₂ and CO molecules over the full composition range for four representative gas mixtures: (a) CO₂/H₂O, (b) CO₂/CH₄, (c) CH₄/H₂ and (d) CO/C₂H₄, at T_gas = 2000 K.  These four gas mixtures are also shown as lines (a)‑(d) crossing a Bachmann diagram in Figure 5.16.  The calculated compositions are considered in turn, first from the perspective of the CH₃ radical which is generally considered to be the primary growth species in most low‑pressure diamond CVD environments [[16],[17]].

 

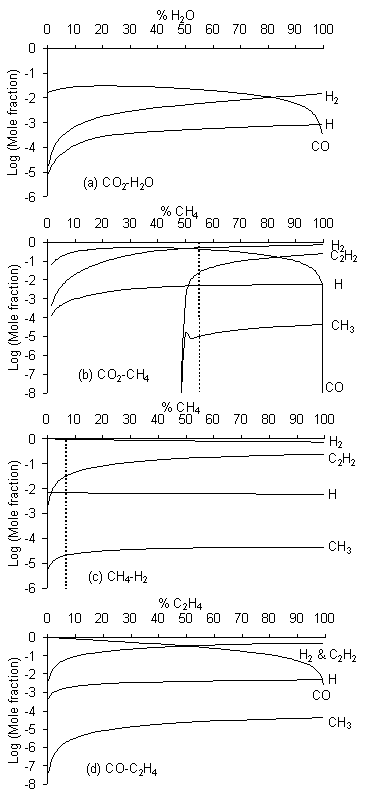
Figure 5.15.Calculated species mole fractions for T_gas  = 2000 K over the full range of mixing ratios for four different gas mixtures: (a) CO₂/H₂O; (b) CO₂/CH₄; (c) CH₄/H_2; and (d) CO/C₂H₄.  The composition for which [H]/[C₂H₂] = 0.2 is denoted by a vertical dotted line in (b) and (c).

 

Figure 5.15(a) illustrates that the CO₂/H₂O gas mixture is comparatively unreactive; the CH₃ mole fraction (denoted as [CH₃]) is negligible (< 10^‑10) for all compositions and, consequently, no production of C₂H₂ (the most stable product from CH₃ radical recombination) is seen.  The chemistry prevailing in CO₂/CH₄ gas mixtures (Fig.5.15(b)) has already been discussed in some detail (Section 5.7).  We find [H₂], [CO] and [H] are relatively high over the entire range of compositions, but [CH₃] is < 10^-10 at all compositions below 50% CH₄ (i.e. >50% CO₂).  As soon as the [CH₄]/[CO₂] input gas ratio exceeds unity, [CH₃] is predicted to rise sharply (to >10^-6) and the C₂H₂ mole fraction grows rapidly.  For the CH₄/H₂ gas mixture (Fig.5.15(c)) the [CH₃] >10^-6 over the entire composition range, as it is for the CO₂/C₂H₄ gas mixture after addition of just a few percent of ethene (Fig.5.15(d)).  In both cases, [C₂H₂] rises rapidly with increasing hydrocarbon. 

 

Figure 5.16 shows that for these four mixtures, and for all the other gas mixtures studied, the input gas compositions at which [CH₃] jumps up to values ~10^-7 lie along the H‑CO tie line.  Gas mixtures giving [CH₃] <10^-7 lie in the no-growth region below the H‑CO tie line (e.g. the CO₂/H₂O gas mixture shown as line (a)) while all points representing gas mixtures yielding [CH₃] >10^-7 fall above the H‑CO tie line.  The existence of the no-growth region in regions where [C]/[O] < 1 is thus readily explained by the low CH₃ radical densities in gas mixtures that fall within this part of the Bachmann diagram.  A similar step of ~6 orders of magnitude was observed in C₂H₂ concentration, as seen in Figures 5.10(b), (c) and (d).  This correlation is due to the rapid recombination of CH₃ radicals [[18]] leading to the formation of C₂H₂.  However, we prefer to define the lower boundary of the diamond domain in terms of [CH₃] because methyl is generally considered to be a diamond growth precursor [16,17], whereas C₂H₂ is linked to the deposition of graphite [[19]].  These calculations also serve to reinforce the suggestion of Beckmann et al [[20]] that oxygen controls the concentration of reactive carbon species present in the gas phase.  Reaction of oxygen and hydrocarbons results in the relatively high concentrations of both CO and H₂ seen in Figures 5.15(a) and 5.15(c) [15].  Significant CH₃ concentrations are only produced and build up in gas mixtures lying above the H‑CO tie line, where [C] > [O].  The H‑CO tie line is therefore the lower boundary of the diamond deposition domain.

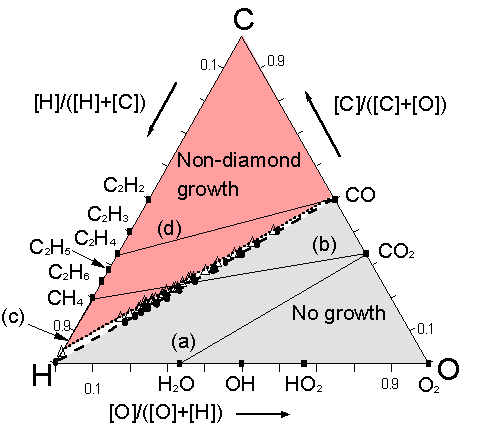
Figure 5.16. C-H-O phase diagram for diamond CVD.  Gas mixtures investigated in this work lie along the tie lines linking CO, CO₂, O₂ and each H_xO_y species with each hydrocarbon moiety (each represented by a n symbol), and along the C‑H axis for the case of the CH₄/H₂ and C₂H₂/H₂  gas mixtures.  The full lines cutting across the diagram correspond to the four gas mixtures (a) CO₂/H₂O, (b) CO₂/CH₄, (c) CH₄/H₂ and (d) CO/C₂H₄ illustrated in Fig. 5.15.  The dashed (‑  ‑  ‑) and dotted (-----) lines indicate the C‑O tie line (which forms the boundary between the no-growth and diamond growth regions), and the boundary between diamond and non-diamond growth regions, respectively.  Key: = = composition where, for any given gas mixture, the CH₃ mole fraction increases from ~10^-10 to ~10^-6, D = composition for which [H]/[C₂H₂] = 0.2 at T_gas = 2000 K.

 

The upper boundary of the diamond domain separates the diamond growth and non-diamond growth regions.  The distinction between these two regions is less easy to define, and the corresponding boundary is thus less sharp.  Here we have assumed that, in order to obtain good quality diamond growth, H atoms must be present at concentrations that are high enough to enable etching of non-diamond phases (often associated with deposition of unsaturated hydrocarbons), and therefore that the boundary between diamond and non-diamond growth must fall at compositions where the ratio of atomic H to unsaturated hydrocarbons exceeds some critical value.  Since C₂H₂ is the most abundant unsaturated hydrocarbon arising in the simulations, we investigated the ratio [H]/[C₂H₂] at T_gas = 2000 K for all 38 gas mixtures and all mixing ratios.  We have already shown that [CH₃] is negligible (<10^‑10) throughout the entire composition range of the CO₂/H₂O gas mixture (Fig.5.15(a)); C₂H₂ is therefore not formed, and the [H]/[C₂H₂] ratio is much greater than unity.  For CO₂/CH₄ gas mixtures (Fig.5.15(b)), the [H]/[C₂H₂] ratio is similarly large for small CH₄ additions, but declines rapidly once the input mole fraction of CH₄ exceeds 50%, reaching a value of 0.2 when the CH₄/CO₂ mixing ratio is 55/45 and T_gas = 2000 K.  This is the input gas ratio which, experimentally, we judged to represent the boundary separating diamond from non-diamond growth [5].

 

This encouraged us to explore at what input compositions other gas mixtures yielded [H]/[C₂H₂] ratios of 0.2.  In the case of CH₄/H₂ mixtures (Fig.5.15(c)), [H]/[C₂H₂] declines with increasing CH₄ additions and passes through the value 0.2 at ~7% added CH₄, while for the CO/C₂H₄ mixture (Fig.5.15(d)) the [H]/[C₂H₂] ratio never attains a value of 0.2.  The open triangles in Fig.5.16 indicate the full range of gas mixing ratios for which [H]/[C₂H₂] = 0.2.  Very clearly, they lie along a straight line which matches well with the diamond/non-diamond growth boundary deduced from the experimental observations of Marinelli et al [[21]].  Gas compositions below this line give [H]/[C₂H₂] > 0.2 while those above it give [H]/[C₂H₂] < 0.2.  Gas mixtures lying above both the H‑CO tie line and the [H]/[C₂H₂] = 0.2 line fall within the non-diamond growth region (e.g. the CO/C₂H₄ gas mixture shown as line (d)), while mixtures like CO₂/CH₄ which cut through both boundary lines on the Bachmann diagram can support compositions which lie in the no-growth ([CH₃] <10^-7), non-diamond growth ([H]/[C₂H₂] <0.2) and diamond growth ([CH₃] >10^-7 and [H]/[C₂H₂] >0.2) regions. 

 

As Table 5.3 shows, such analysis allows prediction of the composition process window for good quality diamond growth for all of the various stable input gas mixtures in this study.  Agreement with experimental observation is generally very good, except for the case of CO₂/C₂H₂, where theory predicts that both the no‑growth/diamond and diamond/non-diamond growth boundaries occur at slightly lower C₂H₂ mixing ratios than experiment [21], and for the case of CH₄/H₂ gas mixtures, where the [H]/[C₂H₂] = 0.2 criterion admits CH₄ mole fractions higher than the ~3% upper limit generally found for reasonable quality diamond deposition [[22]].

 

	% Hydrocarbon
	No-Growth/Diamond Growth Boundary		Diamond/Non-Diamond Growth Boundary
Mixture	Calculated	Experiment	Calculated	Experiment
C2H2 / CO2	33.5	(32.0 – 32.7) a)	35.0	(32.7 – 33.4) a)
C2H4 / CO2	33.5	(32.1 – 35.1) a), 33 b)	36.1	(35.1 – 37.1) a), 35 b)
C2H6 / CO2	33.5	(32.5 – 34.2) a)	37.0	(34.2 – 39.4) a)
CH4 / CO2	50.0	(47.7 – 49.1) a), 50 b)	55.0	(49.1 –56.3) a), 52 b)
C2H2 / H2O	33.5		36.3
C2H4 / H2O	33.5		37.1
C2H6 / H2O	33.5		37.0
CH4 / H2O	50.0		56.1
C2H2 / O2	50.0		51.5
C2H4 / O2	50.0		52.5
C2H6 / O2	50.0		53.4
CH4 / O2	66.5		70.5
CH4 / H2	0		7.4	(3 – 4) c)

a)      Ref. 21,

b)      Ref.6,

c)      Ref. [23] (and references therein).

 

Table 5.3. The position of the no-growth/diamond growth and diamond/non-diamond growth boundaries are predicted for a range of gas mixtures in terms of % hydrocarbon (e.g. %C₂H₂ for C₂H₂/CO₂).  These boundaries are compared with the results of some of the available deposition experiments.  Simulation conditions: temperature 2000 K, pressure 40 Torr, simulation time length 5 s.

 

Two final points merit comment.  Firstly, the particular value of the [H]/[C₂H₂] ratio used as the criterion for separating the diamond and non-diamond growth regions is, of course, arbitrary, and also temperature dependent.  However, as Figure 5.17 illustrates, all of the various input gas compositions identified as lying on this boundary exhibit precisely the same temperature dependent [H]/[C₂H₂] ratio at T_gas ³ 1900 K - emphasising, once again, the very similar gas phase environment established upon activation of the various gas mixtures used for diamond CVD - and show only minor divergence at lower gas temperatures.  Such plots also allow further illustration of the way in which just a small change in mixing ratio can dramatically effect the [H]/[C₂H₂] ratio and, thus, the resulting film composition. 

 

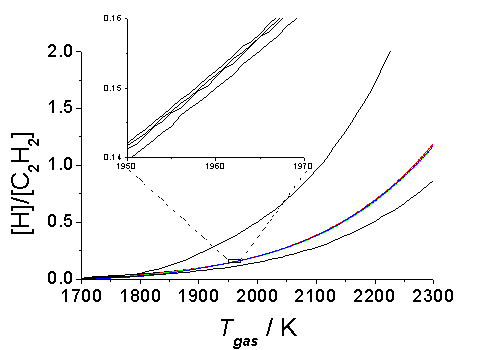
Figure 5.17. Plot showing the temperature dependence of the [H]/[C₂H₂] ratio for six different input gas mixtures.  The central curve is actually 4 superimposed curves (as shown by the inset expanded plot) for the gas mixtures: 55%CH₄/45%CO₂; 7%CH₄/93%H₂; 51%C₂H₄/49%CO₂; 36%C₂H₂/64%CO₂, each of which is identified as lying on the diamond/non-diamond growth boundary.  The curves at higher and lower [H]/[C₂H₂] values correspond to 52%CH₄/48%CO₂ and 57%CH₄/43%CO2 gas mixtures, respectively

 

For the specific case of CO₂/CH₄ gas mixtures, we identify a 45:55 mixing ratio as the composition corresponding to the diamond/non-diamond growth boundary.  Adjusting the input gas mixing ratio to 48:52 leads to a doubling of the calculated [H]/[C₂H₂] ratio at all temperatures, and moves the process well into the diamond growth region of the Bachmann diagram.  Conversely, a similarly small compositional shift in the other direction - to a 43:57 mixing ratio - leads to a halving of the calculated [H]/[C₂H₂] ratio, and non-diamond growth.  Secondly, however, we note that the present simulations predict the diamond ® non-diamond growth boundary for CH₄/H₂ gas mixtures to lie at 7% CH₄, more than twice the value found experimentally [22].  This may suggest that the criteria governing the boundary between the diamond and non-diamond growth regions may be slightly different for mixtures containing little (or no) oxygen; inspection of Figure 5.16 suggests that further experimental study of diamond growth from CH₄/H₂O - as a function of mixing ratio - could be helpful in this regard.  The fact that a simple model that merely allows a gas mixture to react at a given temperature, pressure and for a set time, has been used to model successfully the boundaries of the Bachmann diagram, indicates that whatever the type of CVD process used (for the conditions investigated) the activation of the gas mixture is a critical process that (along with T_sub) determines whether film growth from a given gas mixture will be successful. 

5.9. References