Section 1

Chapter 1 : Introduction

 

Since its first documented mining in India around the fourth century B.C. diamond has been highly regarded for its brilliance.  In a second century B.C. manuscript it was reported that the Chinese had realised diamond’s “industrial“ use stemming from its unequalled hardness and were importing diamonds from India. 

 

Diamond’s hardness has in turn lent itself to its own name.  The name diamond is derived from the Greek adamaz (adamas), which is translated as ‘unconquerable’, and while used originally to refer to any hardened material such as steel, now refers solely to diamond.

 

It is not surprising then that today diamond is sought after as a jewel and is used in a wide range of industrial applications, for example, grinding, polishing, wear resistant coatings, etc.

 

This chapter opens with a brief summary of the structure and properties of diamond, and of synthetic routes to diamond, based on high pressure high temperature (HPHT) methods and the more recent chemical vapour deposition (CVD) route.  The complex chemistry underpinning the CVD methods of growth is also discussed, as are the present and possible future applications of synthetic diamond.

 

 

1.1       Structure and Properties of Diamond

 

Diamond is simply a 3D network of tetrahedrally bonded sp³ hybridised carbon atoms having a cubic-close packed crystal structure analogous to that of zinc blende.  Each carbon atom is s-bonded to four neighbouring carbon atoms.  This differs from the structure of graphite in which a hexagonal arrangement of s-bonded sp² hybridised carbon atoms exist in 2D sheets, where each sheet is weakly bonded to its neighbour.  This structure attributes itself to the softness of graphite.  These two structures are shown in figure 1.1.

Figure 1.1  The lattice structures of diamond and graphite.  Carbon atoms are noted by the black spheres, s-bonds by the solid lines and weak inter-sheet bonds by the dashed lines.

 

 

While diamond, like graphite, is an allotrope of carbon its scarcity adds to its mystique.  This scarcity, relative to that of graphite, is a facet of a large activation energy preventing thermal conversion from graphite to diamond.  However, the enthalpy of formation of diamond is strangely close to that of graphite, being only 2.9 kJ mol^-1 higher than that of diamond (measured at 298 K and 1 atm).  Diamond, being the denser allotrope of carbon, (r_diamond = 3513 kg m^-3: r_graphite = 2260 kg m^-3 at 293 K) is the most stable at high pressures.

 

Diamond is often referred to as the ultimate engineering material.  Its extreme properties described here make it an attractive engineering material for a large number of applications, some of the most common uses and applications of diamond are described in detail later in this chapter.

 

Diamond’s structure of strong covalent bonds holding a tetrahedral network of carbon atoms makes it the densest and hardest of any known material.  The elastic modulus and compressibility of diamond are also unsurpassed as a facet of its structure; it is robust and resistant to both radiation damage and chemical corrosion.

 

While diamond has a number of extreme physical characteristics, its thermal and electrical properties are also of interest.  Natural diamond is an insulator with a wide band gap of 5.49 eV.  By altering the diamond lattice, with the inclusion of atoms with valences different to that of carbon, it is possible to form both n- and p-type doped diamond.

 

Uncharacteristic to non-metal materials, diamond has an unparalleled thermal conductivity, four times greater than that of copper at room temperature.  Metals are generally good thermal and electrical conductors due to the high mobility of electrons within the lattice.  Undoped diamond having a covalent lattice has very little electron mobility and is therefore an electrical insulator.  However, due to the extremely high degree of rigidity within the structure crystal vibrations (phonons) allow high thermal conductivity.

 

Pure diamond crystals have a very wide optical transparency, ranging from

0.22 mm, in the ultraviolet, to the far infrared.  Due to its high symmetry, very few intrinsic absorbance bands are present, impurities (typically nitrogen) in the lattice represent the main source of absorbance bands.  However, lattice defects reveal optical activity of the electronic and vibrational transitions.

 

Table 1.1 summarises some of the unique properties of diamond.

 

Table 1.1  Intrinsic properties of natural diamond.

 

1.2       Synthesis of Diamond

 

Since Tennant’s realisation in 1776 that diamond is solely a form of carbon[1], and the discovery in the 19^th century that diamond is formed deep in the earth’s crust, many attempts were made to simulate the high pressures and temperatures required using graphite as a carbon source.  It was not until 1954 that the synthesis of diamond by a High Pressure High Temperature (HPHT) technique by the General Electric Company was successful[2].

 

While the production of HPHT diamond and the mining of diamond were providing industrial diamonds predominately for the cutting industry, a new technique for growing diamond at low pressures was also discovered between 1953 and 1954 [3]^,[4].  This new technique involved the Chemical Vapour Deposition (CVD) of diamond from a carbon containing gas precursor at low and atmospheric pressures.  While a number of different growth techniques have been demonstrated the same principle is followed.  Growth is carried out by the deposition of carbon from an activated gas-phase hydrocarbon onto a suitable substrate material maintained at a temperature of between 1000 and 1400 K.  The major differences between the different techniques used are mainly related to how the gas-phase environment is activated.  A description of the most common reactor types follows later in this chapter.

 

1.3       HPHT synthesis of Diamond

 

As mentioned previously, diamond being the densest allotrope of carbon is the most stable form at high pressures.  This fact, together with the knowledge that diamond is formed at high temperatures within the earth’s crust, stimulated research into a HPHT technique for the synthesis of diamond.  The technique, first published in 1954, is still used in the production of industrial grade diamond.  The basis of the formation is the crystallisation of diamond from a melt of metal-solvated carbon at pressures of between 50 and 100 kBar and temperatures ~1800 - 2300 K.

 

While HPHT techniques have so far been used in the synthesis of industrial grade diamond, recent reports by the General Electric Company have confirmed use of a HPHT technique to manipulate the colour centres within natural diamonds for the gem market[5].

 

Unfortunately, HPHT synthesis of diamond suffers from high cost and the inability to produce coatings or films of diamond.  The CVD of diamond therefore has an advantage over HPHT synthesis in that the deposition of diamond is much more flexible, being governed by the design of the reactor.

 

 

1.4       Diamond synthesis by Chemical Vapour Deposition (CVD)

 

The deposition of crystalline diamond from a carbon containing gas mixture was first demonstrated at about the same time as the development of HPHT techniques in the mid-1950’s.  The first attempts at diamond CVD at pressures less than an atmosphere resulted in extremely low deposition rates and were restricted to growth onto diamond substrates.  Patent applications by Eversole[6] of the Union Carbide Corporation in 1962 outlined the low pressure CVD technique used, this was far superior to earlier techniques that also produced large quantities of graphitic carbon.  Angus et al.³ improved Eversole’s technique by discovering that atomic hydrogen preferentially etches deposited graphite over diamond.  It was not until 1981, however, that Spitsyn et al.[7] succeeded in depositing diamond onto substrates other than diamond at growth rates of approximately 1mm hr^-1.  During the early 1980’s growth rates were improved by a number of research groups and companies by studying various growth techniques to optimise the diamond deposition conditions[8]^,[9].

 

The problem associated with understanding how diamond CVD occurs is one of appreciating under what conditions and limitations a metastable material can be grown.  This encompasses a large number of problems in itself, including the nature of the complex gas-phase reactions, and the surface and bulk chemistries of diamond formation.

 

Increased understanding of the CVD process in terms of the activation of the gas-phase environment, the transport of species, and the growth process has fuelled development of the procedure.  The process of diamond CVD, irrespective of the method of production, may be described in a number of separate yet interlinked stages.  The reactants, typically a dilute hydrocarbon / hydrogen gas mixture, are activated forming the important radical species and atomic hydrogen.  The transport of the species to the growing surface is the next consideration; this may occur by convection or by diffusion and is determined by the technique used.  At the growing surface, the gas-surface interactions initiate the necessary surface chemistry.  Diamond growth is possible if the substrate temperature is maintained at between 1000 and

1300 K.  This process is summarised in figure 1.2.

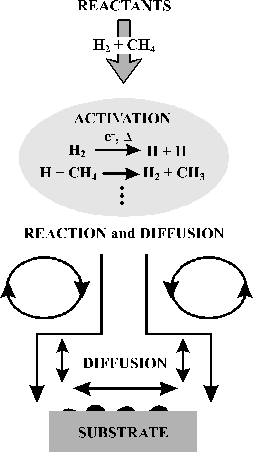
Figure 1.2  Schematic representation of the diamond CVD scheme adapted from a review article by Goodwin and Butler[10]

 

 

In the next chapters the gas-phase and surface chemistry will be discussed in terms of a low power CVD reactor.  Such reactors have been studied in more detail than DC-arcjet systems where high reactant flux and gas temperatures may present subtle differences in the relative mole fractions and transport of species.  The discussion will also be limited to low-pressure reactors, however recent results from high-pressure (above one atmosphere) CVD systems have demonstrated very high growth rate and quality deposition[11].

 

 

1.5       Gas-phase chemistry

 

Diamond CVD is most commonly carried out with a reactant gas mixture of approximately 1-2% methane in hydrogen.  Although it is known that diamond growth is relatively unaffected by the carbon source gas used[12]^,[13], methane or acetylene are most commonly employed.  In order to initiate reactions in the gas-phase it is necessary to activate the gases, this may be carried out by a number of different methods and defines the technique used.  While the different CVD methods will be discussed in detail later in this chapter, the activation of the gas-phase reactants may involve thermal activation (e.g. a hot filament), use of an electrical discharge (e.g. microwave, DC or RF) or by flame (e.g. oxyacetylene torch).  The activation of the gas mixture, irrespective of the method used, produces atomic hydrogen.  Atomic hydrogen is the driving force behind the gas-phase and surface reactions and is clearly one of the most important species present in terms of diamond film growth and quality.

 

The majority of studies of the gas-phase and growth process have been carried out in a hot filament system (see Chapter 1.8.1) and, while a number of factors discussed here may be technique-dependant, it is thought that, in general, the results obtained may be applied to diamond deposition as a whole.

 

 

1.5.1   Atomic hydrogen production

 

In hot filament systems, atomic hydrogen (from herein also referred to as H atoms) is produced heterogeneously on a hot filament surface via thermal decomposition, shown in reaction 1.1.

 

H₂   ®  2H                                         Reaction 1.1

 

The H atoms diffuse rapidly into the reactor.  The atomic hydrogen concentration, [H], at the filament surface scales approximately as would be expected for thermal equilibrium.  However, measurements of the atomic hydrogen absolute concentration show that only between 12%[14] and 60%[15] of the expected [H] exists for a given filament surface area, filament material, reactor pressure and hydrocarbon content.  This has been attributed to the rapid diffusion of atomic hydrogen from the filament surface to cooler regions of the reaction chamber.  For this reason, in the cooler regions of the reactor a super-equilibrium of atomic hydrogen exists.  Process pressures, typically being below 1 atmosphere, also maintain the atomic hydrogen super-equilibrium by causing atomic hydrogen recombination in the gas phase to be a slow process.

 

The production of atomic hydrogen within plasma-enhanced reactors (such as microwave and DC-arc) is achieved via direct coupling of energy into the free electrons within the plasma.  This produces H atoms homogenously via reaction 1.2 shown.

 

H₂  + e^-  ®  H  +  H  +  e^-                              Reaction 1.2

 

This reaction occurs through successive vibrational excitation of H₂ by electron impact.

 

It is worth noting that in regimes where the pressure exceeds 100 Torr it is thought that through inelastic collisions electrons may be able to transfer energy to heavy particles.  This will result in heating of the gas, leading to H₂ dissociation by impact with heavy particles, M, via the general reaction 1.3

 

H₂  +  M  ®  2H  +  M                                   Reaction 1.3

 

At these temperatures (~ 3000 K) the production and loss rates of H atoms are such that an equilibrium value may be reached for the local gas temperature.

 

Plasma-enhanced reactors have a distinct advantage over hot filament systems in terms of H atom production, as the active surface area of the filament restricts the production of H atoms.  It has long been understood that under conditions of high gas-phase carbon content the filament surface becomes poisoned.  This occurs due to the growth of a graphitic layer on the filament from a gas-phase environment, in which the carbon content surpasses the solubility limit in hydrogen.  The solubility limit is a function of the filament temperature and inhibits the catalytic effect of the filament.

 

 

1.5.2   Atomic hydrogen loss mechanisms

 

The production and loss rates of atomic hydrogen in a reactor are such that a steady state regime exists.  The destruction of H atoms, assuming no atomic hydrogen leaves the reaction chamber, occurs mainly via either homogenous or wall recombination mechanisms.

 

The homogenous recombination of atomic hydrogen, under typical conditions prevailing in a CVD reactor, occurs at a slow rate.  This further allows the super-equilibrium of atomic hydrogen to exist at low local temperatures, thus supporting the transport of H atoms to the growing surface or the reactor chamber walls.  The homogenous recombination occurs via reaction 1.4,

 

H  +  H  +  M  ®  H₂  +  M                                        Reaction 1.4

 

where M is a third body, facilitating the removal of excess heat of recombination.  This reaction rate is pressure dependant with a characteristic reaction time at a pressure of 20 Torr of the order of 1 s [16]^,[17].

 

The presence of a small quantity of hydrocarbon, typically methane, presents a removal route for H atoms via the gas-phase reactions.

 

H  +  CH₃  +  M  ®  CH₄  +  M                                 Reaction 1.5

 

H  +  CH₄  ®  CH₃  +  H₂                                         Reaction 1.6

 

These two reactions compete with reaction 1.4 and hence determine the recombination rate of atomic hydrogen.

 

The most important route for the loss of H atoms is heterogeneous recombination.  This may occur either as the atomic hydrogen impinges on the reactor walls, or due to collision with the growing diamond surface.  Studies have shown the growing diamond surface acting as an H atom ‘sink’, the concentration profile at the substrate surface being a function of the substrate temperature¹³.  The loss of H atoms to a diamond surface may be expressed in term of the recombination coefficient, g_H, which is defined as the atomic hydrogen loss rate at the surface divided by the H atom collision rate with the surface.  Experimental[18] and theoretical[19] measurements of this factor have all been in agreement.  Krasnoperov et al.[20] measured g_H over a wide substrate temperature range, establishing the functional form shown in figure 1.3.

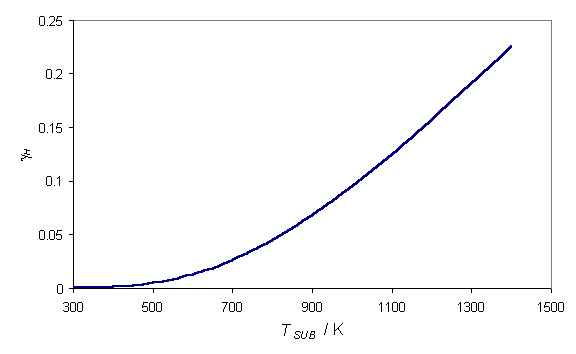Figure 1.3  Graph showing the recombination coefficient of H at the diamond surface as a function of T_sub adapted from reference 10.

 

 

At substrate temperatures, typically used during diamond CVD (~1000-1300 K), the recombination coefficient is high, signifying that the surface is acting as a sink for H atoms.  The recombination reaction,

 

2H  ®  H₂                                          Reaction 1.7

 

is exothermic (104 kcal mol^-1) and in many reactor systems is the major contributor to heating the substrate.

 

 

1.5.3   Hydrocarbon Gas-phase Chemistry

 

The role of atomic hydrogen is also one of ‘fuelling’ the hydrocarbon gas-phase chemistry.  In the gas-phase, atomic hydrogen participates in a number of abstraction reactions of the hydrocarbon reactant and its ‘abstracted’ species.  Figure 1.4 summarises the principal production and loss routes of carbon species in a CVD reactor operating with a CH₄/H₂ gas mixture.

 

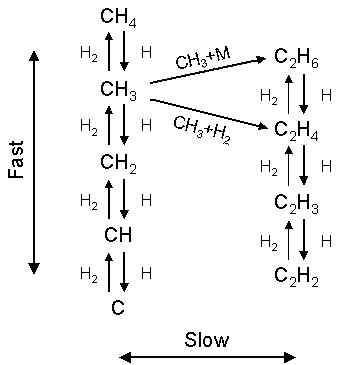
Figure 1.4  Principal C₁ and C₂ gas-phase reaction scheme illustrating the fast hydrogen shift reactions and the slower bimolecular C₁ to C₂ hydrocarbon forming steps.  Adapted from reference [21].

 

It is worth noting that this reaction scheme only deals with C₁ and C₂ species.  While C₃ and higher species are present in the gas-phase, it is thought that the relative concentrations of these species are sufficiently low so as not to influence the reaction scheme shown[22].  Hydrogen and atomic hydrogen, being the major gas-phase species present in the reactor, dominate the reactions, with the hydrogen transfer reaction rates being generally greater than those describing the bimolecular hydrocarbon reaction rates.

 

The series of interconnected hydrogen shift reactions (left-hand column of figure 1.4) occur rapidly in both the forward and reverse directions due to low activation energies.  The rate of reaction between atomic hydrogen and any carbon-containing species will obviously be a function of the local gas temperature and the local atomic hydrogen concentration.  This relationship defines the production and distribution of C₁ species throughout the reactor.

Due to the complex nature of the reaction scheme and the gas temperature gradients that exist within a CVD reactor, studies of the gas-phase environment are deemed necessary to improve our understanding of this system.  The first hydrocarbon concentration measurements of the diamond CVD environment were carried out by Celii et al.[23] using an infrared diode laser absorption technique to detect acetylene, methyl radicals and ethylene in a hot filament reactor.

 

This study found that high concentrations of CH₄ and C₂H₂ existed together with low concentrations of CH₃ and C₂H₄ from an input CH₄ / H₂ gas mixture.  Bearing in mind that the absorption technique used sampled a column of inhomogeneous gas, a rotational temperature of ~600 K was obtained from C₂H₂ detection.  This reflects an average gas-phase temperature ranging from the hot filament to the cold reactor walls.

 

Simple gas-phase equilibrium calculations as in figure 1.5 for a 1% CH₄ / H₂ gas mixture, clearly show that the conversion of CH₄ to C₂H₂ occurs at gas temperatures that exist during diamond deposition.

 

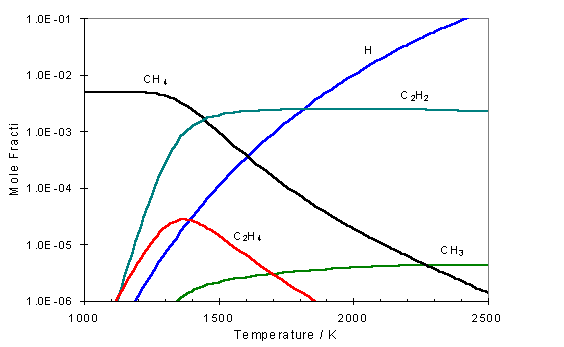
Figure 1.5  Gas-phase equilibrium calculation carried out using the CHEMKIN computer package[24] for a 1% CH₄/H₂ gas mixture using GRI-MECH 3.1[25] reaction rate constants

 

The study concluded that a significant fraction of the CH₄ is converted into C₂H₂ at high gas temperatures within the reactor.  The concentrations of acetylene measured in this study represented a 10-20% conversion from methane.  Since this conversion occurs via a number of sequential reactions each involving atomic hydrogen, it was recognised that a complex gas-phase chemistry scheme must exist within the CVD reactor.

 

Subsequent studies of the gas-phase chemistry in both hot filament and microwave systems by a number of detection methods have given an indication of the gas composition.  One interesting feature resulting from these studies is that the mole fractions of carbon containing species in the activated gas are essentially independent of the input carbon-containing precursor.  Molecular-Beam Mass Spectrometry (MBMS) studies carried out by Tsang et al.[26] have shown this independence for input gas mixtures of CH₄/H₂, C₂H₄/H₂ and C₂H₂/H₂ in a hot filament reactor as a function of filament temperature (for a filament temperature > 2200 K).  The results of this study are shown in figure 1.6.

 

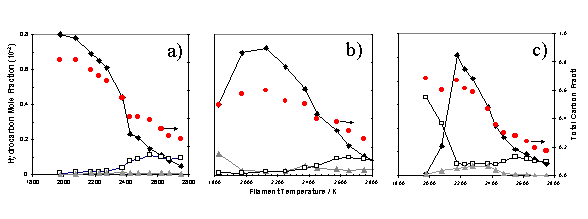Figure 1.6  MBMS results showing the mass fractions of stable species as a function of filament temperature, measured 6mm from the filament surface in a hot filament CVD reactor operating on gas mixtures of a) 1% CH₄ / H₂ b) 0.5% C₂H₄ / H₂ and c) 0.5% C₂H₂ / H₂.   Symbols shown relate to CH₄ (¨), C₂H₂ (o) and C₂H₄ (p).  The carbon balance (l) is shown to decrease with increasing filament temperature being a consequence of the Soret effect.

 

 

The conversion of a C₁ species to a C₂ species is carried out via rapid H atom abstraction.  If, for example, methane is introduced into a reaction scheme whereby the H/H₂ fraction is below a few percent, methyl radicals (CH₃) may be formed via reaction 1.8

 

H  +  CH₄  ¾  CH₃  +  H₂                               Reaction 1.8

 

Recombination of these methyl radicals will go to form C₂ species via the reactions,

 

CH₃  +  CH₃  ¾  C₂H₆                                    Reaction 1.9

 

CH₃  +  CH₃  ¾  C₂H₅  +  H                           Reaction 1.10

 

CH₃  +  CH₃  ¾  C₂H₄  +  H₂             Reaction 1.11

 

Once the C₂ species is formed it is rapidly converted to the thermodynamically favoured stable species C₂H₂ via the reaction scheme:

 

C₂H₆  +  H  ®  C₂H₅  +  H₂                           Reaction 1.12

C₂H₅  +  H  ®  C₂H₄  +  H₂                           Reaction 1.13

C₂H₅  +  M  ®  C₂H₄  +  H  +  M                   Reaction 1.14

C₂H₄  +  H  ®  C₂H₃  +  H₂                           Reaction 1.15

C₂H₃  +  H  ®  C₂H₂  +  H₂                           Reaction 1.16

C₂H₃  +  M  ®  C₂H₂  +  H  +  M                   Reaction 1.17

 

Modelling studies, like those used in deriving figure 1.5, indicate that no analogous gas-phase process exists that allows the conversion of acetylene, a C₂ species into a C₁ species.  This is clearly in disagreement with experimental studies and has prompted some to postulate that the conversion may occur heterogeneously on the reactor wall surface¹⁰.  Since a portion of this thesis deals with experimental studies into this problem, further discussion will be presented in chapter 3.

 

From modelling studies carried out by Dandy and Coltrin[27], it is clear that CH₃, the methyl radical, is the most abundant C₁ radical species present in the gas-phase, under typical low power CVD process conditions.  Methyl radicals are formed, via reaction 1.8.  While numerical simulations show this reaction to be in partial equilibrium at distances greater than 1 mm from the substrate surface, close to the surface the comparative lack of H atoms, due to surface recombination, causes the partial equilibrium to collapse.

 

Mass spectroscopy studies carried out by Harris et al.²², using a quartz sampling tube, positioned at the surface of either silicon or platinum substrates, have shown that CH₄ and C₂H₂ are the main species present at a growing surface.  The analysis of the gas-phase composition confirms a non-equilibrium nature at the substrate surface.  The concentrations of species such as CH₄, C₂H₂, CH₃ and C₂H₄ were measured and found to be sufficient to account for diamond deposition.  Larger hydrocarbons (i.e. C₃ and greater) were present in trace quantities only and therefore deemed unimportant for diamond growth.

 

Resonance Enhanced Multiphoton Ionisation (REMPI) techniques (described in detail in appendix 1) have been used in a number of studies for the detection of H and CH₃, both thought to be important species in the diamond growth environment in a hot filament CVD reactor.  Early REMPI studies[28] showed how the filament temperature influences the H atom production.  The studies concluded that the atomic hydrogen concentration increases monotonically with increasing filament temperature.  For gas mixtures with high CH₄/H₂ fractions the increase is less pronounced, this can be explained by carbon deposition on the filament surface¹⁰.

 

 

1.5.4       Influence of trace non-hydrocarbon additions on gas-phase chemistry

 

Several studies have reported enhanced growth rates and / or quality due to the addition of trace amounts of non-hydrocarbon gases (such as oxygen[29]^,[30], nitrogen[31] and halogens[32]) into a diamond-depositing reactor.

 

Reports of enhanced growth as a result of adding oxygen to a hydrocarbon gas mixture have predominantly focused on microwave based CVD systems[33], similar effects have been demonstrated in a DC-arcjet reactor[34].  Comparable experimental studies have also been carried out in a hot filament system[35], but it is worth noting that even trace quantities of oxygen will oxidise and ultimately destroy a filament.

 

Since the complex carbon-oxygen-hydrogen chemistry involved is beyond the scope of this thesis only a brief outline will be given here.  The gas-phase production of CO via oxidation of acetylene as shown in reaction 1.18 is highly exothermic with a free energy of reaction (DG⁰) = -136.6 kcal mol^-1 at 1000K.

 

C₂H₂  +  O₂  ¾  2CO  +  H₂                           Reaction 1.18

 

This reaction together with the analogous reaction 1.19,

 

            2CH₄  +  O₂  ¾  2CO  +  4H₂                        Reaction 1.19

 

which also possesses a large negative DG⁰, dominate the carbon-oxygen chemistry as at gas-phase temperatures typical within CVD reactors the equilibria of both above reactions lies far to the right.

 

By analysing published experimental data Bachmann et al.[36] were able to characterise a regime in which diamond deposition occurs within a narrow range of C/H/O gas compositions.  The Bachmann triangle (also known as the C/H/O diagram) identifies a tie-line in the ternary system corresponding to high quality growth at high growth rates.  The tie-line points to a link between the growth mechanism and a 1:1 carbon/oxygen ratio in the input gas mixture.

 

The influence of the addition of nitrogen (and other nitrogen containing species, such as NH₃) into a carbon-hydrogen gas mixture at gas temperatures over 600 K is complex and will be investigated and discussed in detail in Chapters 4 and 6 in reference to studies in Hot filament and DC-arc CVD reactors.

 

 

1.6       Surface Growth of Diamond

 

While atomic hydrogen is the main initiator of the gas-phase chemistry it is also crucial at the growing surface.  With hydrogen and atomic hydrogen being the major constituents of the gas-phase environment the diamond surface will be mainly hydrogenated.  The surface will therefore have a fraction of open non-hydrogenated sites, which are regulated by the dynamic equilibrium between the two surface reactions,

 

C_DH  +  H  ®  C_D^*  +  H₂                               Reaction 1.20

 

C_D^*  +  H  ®  C_DH                                          Reaction 1.21

 

where C_DH signifies a hydrogen terminated surface site and C_D^* a non-terminated surface site.  The thermal desorption of H from the diamond surface (the reverse of reaction 1.21) may be ignored as the C-H bond strength is high.  Studies by Goodwin[37] have shown that the formation of hydrogen terminated surface sites occurs principally as a result of reaction 1.21 rather than the reverse of reaction 1.20, for H atom mole fractions greater than 10^-4.  Such a conclusion is based on the fact that, under typical CVD conditions, the H atom mole fraction at the substrate surface is generally greater than 10^-3.

 

A review article by Goodwin and Butler¹⁰ shows that by balancing the C_D^* production and loss rates from reactions 1.20 and 1.21, a value of the fraction of open sites, f, may be obtained using equation 1.1,

 

                                        Equation 1.1

 

where g₁ is the abstraction probability via reaction 1.20, and g₂, is the adsorption probability from reaction 1.21.

 

Both graphite and diamond will, to some extent, be co-deposited within a CVD environment.  Angus et al.[38] showed that atomic hydrogen preferentially etches graphite approximately 50 times faster than diamond at typical growth temperatures, explaining why high purity CVD diamond is obtained by using high H:C input gas ratios.

 

As already mentioned, atomic hydrogen terminates the dangling-bonds present at the growing surface.  This is important since by terminating the surface the reconstruction of diamond to graphite is inhibited.  The surface termination is also believed to enhance nucleation.

 

Growth mechanisms have been proposed for many hydrocarbon species.  Growth onto the various surfaces of diamond, typically defined by their Miller indices, has been shown to occur at growth rates based on the lattice energy and the steric hindrance during addition.  Semi-empirical quantum mechanical calculations have been carried out to measure the energy path of diamond growth onto a hydrogenated (111) surface[39].  The lowest energy scheme was shown to be initiated by the monolayer (111) surface coverage by methyl groups, which consequently forms a lattice via the incorporation of a methyl radical or cation.  However, it has since been shown that steric effects between the surface terminating methyl groups prevent this scheme[40].

 

Further growth studies concentrating on C₁ species addition to the (111) surface have concluded that similar steric difficulties exist.  The addition of C₁ species onto a diamond surface was shown to be ‘optimised’ for the hydrogenated (100) surface where only one carbon is required to form two bonds to the surface.  The hydrogenated (100) surface has been shown theoretically to exist in two forms, the dihydride surface, denoted (100)-(1x1):2H, and the monohydride surface, (100)-(2x1):1H.  However, the dihydride surface consisting of closely neighbouring hydrogen atoms is subject to huge steric strain.  This has since been proven by studying grown (100) CVD films using Scanning Tunnelling Microscopy and Atomic Force Microscopy[41], and successive low-energy electron diffraction and high-resolution electron energy loss measurements[42].

 

Garrison et al.[43] and Huang and Frenklach[44] have proposed growth schemes based on the addition of methyl radicals onto a monohydride (100) surface.  The Garrison mechanism outlined in figure 1.7 proceeds via an initial surface hydrogen abstraction followed by the addition of a methyl radical. 

 

 

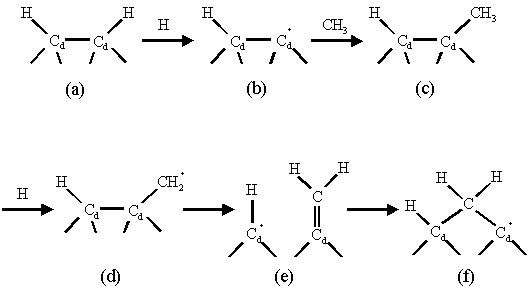
Figure 1.7  The Garrison mechanism for dimer opening and carbon insertion allowing growth to the (100) surface.  This mechanism was adapted from reference 10.

 

Further hydrogen abstraction occurs from the methyl group forming a primary intermediate for a b-scission reaction.  b-scission reactions are thought to play an important part in the etching of non-diamond carbon and in promoting the growth of single atomic diamond layers.  Figure 1.8 schematically illustrates a b-scission reaction mechanism occurring at a surface methyl group.

 

 

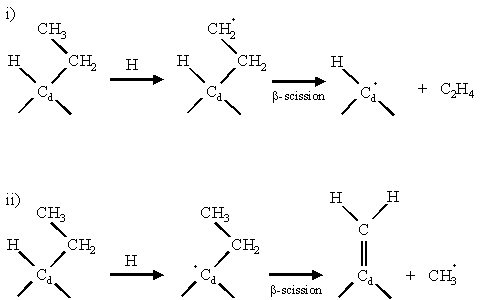
Figure 1.8  b-scission reaction mechanisms adapted from reference [45].  Two possible ways to attack a surface-bonded ethyl group are shown.  An H atom is first abstracted by gas-phase H to create a radical site.  In scheme (i) a methyl hydrogen is abstracted, whereas in scheme (ii) a hydrogen on the diamond surface carbon (C_d) is abstracted.  Both schemes cause the b-carbon bond to break, allowing double bond formation to the carbon from which the hydrogen was abstracted.

 

The radical site and the methylidene intermediate subsequently react to develop a bridging carbon.

 

The mechanism proposed by Huang and Frenklach differs only in that the final stage is reached via a triangular intermediate stage bypassing the b-scission reaction, however an activation energy for the formation of the intermediate state of ~230 kJ mol^-1 suggests the b-scission route is more favourable.

 

While the Garrison mechanism is now generally accepted for growth onto a (100) surface various adaptations have been proposed.  Harris and Goodwin[46] adapted the mechanism to take into account bridging between dimers after insertion.  Thermochemical analysis of this process revealed that, while the distance between two adjacent dimer carbon atoms is too large to be bridged by the methylidene intermediate, successive addition via the Garrison mechanism significantly reduces the carbon-carbon distance allowing bridging to occur.  The revised mechanism predicts growth rates in good accord with those measured experimentally and serves to support the methyl radical in a growth role.

 

 

1.7       Applications of Synthetic Diamond

 

Synthetic diamond produced by HPHT and CVD methods has proven useful in a number of applications which, in general, utilise its extreme properties.  While the use of diamond has replaced other materials.  The industrial use of natural diamond is restricted by the relative scarcity and cost of obtaining large pieces of diamond necessary for some applications.  Even diamond grit used in the cutting tool industry is produced by the HPHT process, as this is economically more viable than the use of natural diamond.  Although both natural and HPHT diamond have found uses in a number of applications these are limited, since the material is only available as single crystal and the crystal cost increases exponentially with size.  The use of CVD diamond deposition allows the production of continuous diamond films that may be grown onto surfaces other than diamond.  This technology also allows significantly more flexibility, as deposition from the gas-phase can occur onto a number of different shaped and contoured surfaces.

 

 

1.7.1   Cutting and Grinding Tools

 

Diamond being the hardest known material is the obvious choice for the cutting tool industry.  Natural, and more recently HPHT, diamond has been used on coated cutting tools for a number of years.  However single crystal diamond, while being wear-resistant, is also prone to cleave easily.  The use of polycrystalline CVD diamond as a coating on cutting tools would overcome this problem.  CVD diamond coated cutting tools have however only recently become industrial products due to problems associated with the adhesion of the coating[47].  Polycrystalline diamond (PCD), (a term used in the cutting industry, not to be confused with the descriptive term used to specify films polycrystalline in nature) commonly used in cutting inserts, is formed via a multi-stage process.  HPHT diamond particles are compacted with cobalt to form a sintered disc which, after treatment in a high-temperature high-pressure press, is then cut and machined into inserts ready to be soldered onto cutting tools.  PCD, although more robust than traditional tungsten carbide, is not as wear resistant as tool inserts formed from CVD diamond as table 1.2 illustrates.

 

 

Table 1.2  Relative tool lifetimes adapted from reference [48].  Refer to reference for information regarding test conditions

 

Diamond coated tool bits have proven to be versatile being used to machine stone, timber, reinforced plastics, aluminium and other non-ferrous metals.  Diamond cannot be used to machine ferrous metals, nickel-based or titanium-based alloys because of its chemical reactivity with these materials at the high contact pressures and temperatures generated during machining.

 

 

1.7.2   Optical windows

 

Diamond windows, having a broadband optical transparency, have recently become an industrial possibility due to improvements in CVD technology that allow large diameter optical-grade diamond windows to be produced.  The broadband transparency, extreme thermal properties and hardness of diamond lend itself to being used in a number of high power laser or detector window applications.

 

Diamond’s resistance to thermal shock and its transparency in the infrared region has encouraged CVD diamond production for use as a window material in high power IR lasers.  Since diamond has a high thermal conductivity its use in high power lasers prevents local heating of the window, which in turn could lead to failure of the material.  In order to prevent local heating of the window the number of faults must be minimised during growth.  Another use of diamond windows being proposed is as an IR airborne sensor detector window for use on missiles.  Since this may require use in hostile environments (e.g. impact of hail, sandstorms, etc.) involving high wear, diamond is now being considered as a substitute for more conventional IR window materials such as zinc selenide[49].

 

Diamond windows, being transparent to X-rays, are also finding applications as X-ray windows in detectors and tubes.  Diamond may also be used in future lithography techniques for similar reasons[50].

 

 

1.7.3   Thermal Management

 

As the trend for next generation high-power electronic and optoelectronic devices seems to be towards smaller more compact units one major problem that needs to be overcome is the efficient removal of large quantities of generated heat.  By utilising diamonds unequalled thermal conductivity, freestanding thick CVD films could be used as a medium to ‘spread’ the heat from the device to the cooling system.  Diamond has another advantage over other high thermal conductivity materials in that, being a non-metal, diamond is an electrical insulator with obvious advantages in high-density electronic packaging.  CVD diamond films can now be produced having a thermal conductivity in excess of 20 W cm^-1 K^-1 with dimensions suitable for use as a heat spreader in high-power electronics.

 

Recent expansion in the telecommunications industry has involved the use of high-power laser diodes, which produce a large quantity of heat.  Failure of each unit by localised overheating would result in huge financial losses.  Diamond CVD heat spreaders have been used as their relatively high cost is more than compensated by the reduction in losses from unit failure.

 

 

1.7.4   Surface Acoustic Wave (SAW) devices

 

Surface acoustic wave filters are commonly used devices present in televisions, video recorders, mobile telephones, etc.  Introduced electric signal is converted to sound, which is then reconverted into electric signal.  This acts as a filtering system, as higher frequency signal requires a higher frequency sound velocity.  Diamond has become of interest as a high velocity substrate material due to its elastic constant which is the highest known of any material, with a SAW velocity of more than 10000 m/s.  This compares very favorably with analogous ZnO/Sapphire devices (5500 m/s).  Although diamond is not a piezoelectric material, its high acoustic propagation makes it a desirable substrate for SAW devices when coupled with piezoelectric thin films such as ZnO.  Recent research at Sumitomo Electric[51] has produced a Lithium-Niobate (LN) piezoelectric film on a diamond substrate.  It is suggested that the LN/diamond device will have a higher electro-mechanical coupling coefficient than previous devices with high acoustic velocity.  Figure 1.9 shows a schematic of a ZnO/diamond SAW filter.

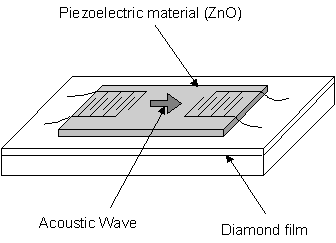
Figure 1.9  Schematic of a Surface Acoustic Wave device adapted from reference [52].

 

While conventional materials are limited by a frequency of 2.5 GHz, it is widely thought that diamond SAW devices will be used in the next generation of high-speed communications.

 

 

1.7.5   Detector devices

 

Conventional photodetectors are generally sensitive to both visible and ultraviolet (UV) light.  This is usually as a result of the band gap of the detector material.  Diamond, having a large band gap (5.49 eV), could effectively be used to detect deep UV light while being blind to visible light.  Being an extremely robust material, diamond would be an excellent candidate for use in hostile environments, such as in environmental monitoring or military applications.

 

While silicon is commonly used as the detector material in particle accelerators, the next generation of accelerators will need to be installed with more robust detectors.  Interest has been shown in diamond due to its resilience to damage[53].  There is also a potential for diamond alpha- and neutron radiation detectors to become widely used in the nuclear industry.  It is likely that CVD diamond devices will become available with high sensitivity and long lifetimes.

 

1.7.6   CVD diamond sensors and electronic devices

 

The many extreme properties of diamond make it an excellent candidate material for micromechanical devices, e.g. pressure and temperature sensors.  Being extremely robust, and having an unparalleled thermal conductivity, diamond seems the obvious choice over more conventional wide band-gap semiconductors such as SiC and III-nitrides.  Diamond, being an electrical insulator, may be doped to form a p-type semiconductor.  This is commonly carried out by incorporation of boron, integrated into the diamond lattice during the growth process.  Boron doped films have an acceptor level 0.368 eV above the valence band.  Problems with forming controllable and stable n-doped diamond films by using the substitutional dopants nitrogen or phosphorus have so far prevented the creation of diamond p-n junctions.  However, for most sensor applications, one type of doping is sufficient.

 

The resistivity of doped diamond decreases with increasing temperature; thus it may be used as the active material in temperature sensors.  Given its thermal conductivity, diamond may also be deposited onto thermocouples providing a robust protective coating for use in harsh environments without the introduction of significant measurement errors.

 

The use of doped diamond films has also been proposed as the active component in pressure sensors.  Thin silicon diaphragms, onto which the diamond is deposited, flex according to the pressure exerted.  The resistivity of the doped diamond film will change as a function of applied stress, a consequence of the piezoelectric effect.  The resistance of the film may then be converted into a pressure reading.

 

Semiconductor manufacturers currently use electrolyte-based detection systems in order to sense the accidental release of toxic doping gases such as PH₃ and AsH₃.  However, it is thought that maintenance costs could be reduced with the introduction of solid-state sensors.  In order to be introduced the active sensor material must be extremely sensitive while being selective against other airborne impurities.  Recent preliminary reports on doped diamond-based devices have shown very high degrees of sensitivity and species selectivity with good detection reproducibility[54].

 

 

1.7.7   Diamond cold cathode emission devices

 

Cold electron emission is observed from metals when a sufficiently high electric field is applied and electrons can overcome the energy barrier to emission from the material.  Wide band-gap materials such as diamond have essentially no energy barrier to electron emission; such materials are referred to having a negative electron affinity (NEA).  In NEA materials, once electrons are excited into the conduction band, they are spontaneously emitted to the vacuum, as the vacuum state is more stable.

Reports of high quantum efficiency photoelectron emission from the (111) surface of natural diamond suggest that diamond-based emission devices could operate at very low power[55].  Research into emission devices using CVD produced films has thus been encouraged.  The development of devices using this phenomenon is ongoing and may lead to the production of flat-panel displays, vacuum microelectronics and microwave amplifiers.  The possible design of such a device is shown schematically in figure 1.10.

 

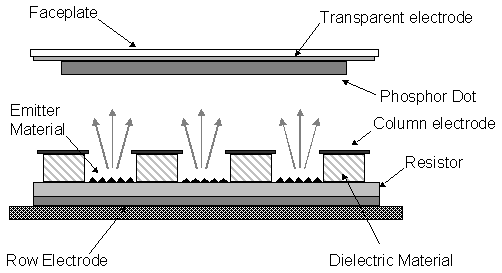
Figure 1.10  Schematic of a diamond–based triode structure cold cathode emission device. 

 

While the possibility of producing such a device seems likely, development has been eclipsed by recent interest shown in similar devices using carbon nanotubes (CNT) as the emitting material[56].

 

 

1.7.8   Other applications

 

A number of niche applications have recently been suggested that utilise diamond’s extreme properties.

 

The company GFD specialises in the production of medical scalpels coated with diamond[57], the scalpels are used in ophthalmic operations requiring extremely sharp high-precision instruments.  Diamond is deposited via CVD methods onto a sharpened silicon blade thereby ensuring the instrument remains sharp throughout its lifetime.

 

Due to diamond’s high wear resistance its use has been suggested as a coating in high wear environments such as the pumping components used in the recovery of crude oil[58].  The pumping of large quantities of crude oil, commonly containing large amounts of abrasive sand, has a detrimental effect on pump components hence requiring frequent replacement.  It is envisaged that diamond CVD coating of components would prolong the lifetime of the apparatus thereby reducing costly repair times.

 

One of the first applications envisaged using CVD diamond was in the formation of speaker diaphragms[59].  Speaker diaphragms require a stiff structure and are formed from materials with high sound velocities.  Natural diamond, with a sound velocity of 18.2 km s^-1, compares favourably with competitive materials (Beryllium: 12.6 km s^-1, Aluminium: 5.1 km s^-1) together with an unsurpassed stiffness.  Manufactured diamond diaphragms, produced via hot filament CVD methods onto a silicon substrate with subsequent etching, have exhibited sound velocities of 16.5 km s^-1 operating at a maximum frequency of 80,000 Hz, the highest generated by any dynamic speaker.

 

While previous estimates of the impact of synthetic CVD diamond may have proven to be over-enthusiastic[60] the last ten years have shown a steady increase in the demand for CVD diamond as more applications are found and the production costs decrease[61].  It seems inevitable that the use of CVD diamond will continue to grow; particularly in the electronics industry.

 

 

1.8       CVD synthesis methods

 

A number of different diamond CVD methods have been developed over the last twenty years, but for a number of reasons, none of these techniques have totally replaced the more traditional hot filament system.  Microwave and plasma jet CVD systems offer the advantage of increased growth rates as compared with hot filament systems, but the versatility, ease of production scale up and economic considerations associated with hot filament CVD reactors encourages their use in the majority of industrial production.

 

 

1.8.1   Hot filament CVD system

 

One of the simplest, cheapest and to some extents most versatile methods of diamond CVD is by a Hot Filament (HF) technique.

 

The major features in a HF system are a resistively heated wire, allowing thermal dissociation of H₂, and a heated substrate.  Figure 1.11 outlines a typical HF system.

 

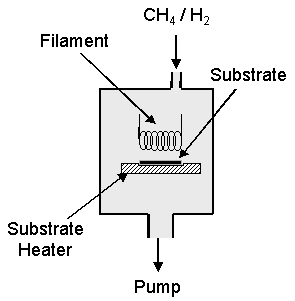
Figure 1.11  Schematic of a typical Hot filament system based on the NIRIM design

 

Originally devised by the NIRIM group, and later developed by Matsumoto et al.[62], the HF system used industrially today has changed very little.  Typically a gas mixture of approximately 1% CH₄ in hydrogen is passed over a heated coiled filament maintained at a temperature between 1800 and 2400°C.  The filament material maybe Tungsten, Tantalum, Rhenium or Molybdenum, the surface of which forms a metal-carbide layer in the presence of the hydrocarbon-hydrogen gas-phase environment.  Thermal dissociation of molecular hydrogen occurs at the filament surface to form atomic hydrogen, which instigates the gas-phase chemistry.   Atomic hydrogen, as mentioned earlier in this chapter, is the main initiator of the hydrocarbon chemistry.

 

Diamond growth occurs on the substrate surface, which is maintained at an optimum process temperature by a substrate heater.  Growth rates of approximately 1 mm hr^-1 are commonly achieved from a CH₄/H₂ input gas mixture using a typical HF system.  Although species transport typically occurs via diffusion from the filament, growth rates of 5 mm hr^-1 have been reported using forced convection[63].

 

HF CVD methods suffer from problems associated with filament material being incorporated into the grown film, the problem being more pronounced with high hydrocarbon gas mixtures.  Studies have shown that, while the increase in hydrocarbon content promotes the growth rate, it also causes increased deterioration of the filament surface.  This will, in effect, prevent the growth of high purity doped diamond films for electronic uses, hence the use of other activation techniques (i.e. microwave enhanced CVD).

 

Due to HF being the most available diamond CVD system, a relatively large number of studies have been undertaken.  These studies have included investigations into the optimum process conditions necessary for high growth and quality deposition.  Zhou et al.[64] has summarised a number of important growth factors.

 

• Increases in the nucleation density may be achieved by pre-treating the substrate.  This leads to the rapid formation of a film due to the improved initial incorporation of growth species.
• While the growth rate may increase with increasing methane fraction in the gas feed (0.1-2%), the non-diamond content of the film also increases.
• Maximum growth rate appears to occur at a chamber pressure of ~10kPa and a substrate temperature of ~850°C.
• The growth rate appears to increase with increasing filament temperature and decreasing filament-substrate separation.  This may be attributed to increased atomic hydrogen concentrations at the substrate surface.

 

Gas-phase studies have attempted to answer a number of questions about the growth environment.  Laser-based diagnostic techniques have been used to study the atomic hydrogen concentrations in a HF reactor.  Celii and Butler[65] used Resonance-Enhanced Multiphoton Ionisation (REMPI) techniques (See Appendix 1) to study the production and destruction of atomic hydrogen in the gas-phase.

 

Probing 8 mm from a tungsten filament at 2500 °C, they observed the atomic hydrogen number density to decrease by an order of magnitude as the methane concentration increased from one to three percent.  Using Laser-Induced Fluorescence (LIF), described in Appendix 2, Schäfer et al.[66] reported a decrease of 30% in atomic hydrogen concentration when the methane concentration increases to 5%.  Atomic hydrogen loss upon addition of hydrocarbon was also shown via Intercavity laser absorption spectroscopy[67], whereby, at low methane concentrations, small increments in the hydrocarbon input resulted in a sharp decrease of the atomic hydrogen number density.  Using Molecular-Beam Mass Spectrometry (MBMS) sampling via a hole in the substrate surface, Hsu[68] showed the concentration of atomic hydrogen to decrease by an order of magnitude when the methane concentration in H₂ increased from 0.4% to 7.2%.

 

These results all go some way to underlining the importance of atomic hydrogen in the gas-phase chemistry.  Atomic hydrogen loss is attributed, to varying extents, to both H atom abstraction reactions, outlined earlier in figure 1.4, and heterogeneous recombination.

 

Heterogeneous recombination of atomic hydrogen takes place via the third-body reaction 1.22.

 

2H  +  M  ®  H₂  +  M                                    Reaction 1.22

 

Being a third-body reaction the rate of recombination will be subject to the gas-phase composition and the gas pressure.

 

Early growth studies showed that diamond films may be grown at comparable qualities and growth rates irrespective of the hydrocarbon feed gas[69].  This discovery led to studies aimed at probing the gas-phase environment to ascertain the species present and to provide evidence of the reactions occurring[70].

 

Studies of the hydrocarbon gas-phase chemistry have focused on suggestions that the methyl radical, CH₃, or acetylene, C₂H₂, may be viable growth species[71].  Celii et al.[72] used infrared diode laser absorption spectroscopy to detect both CH₃ and C₂H₂ in a HF reactor.  Vibrational spectra of C₂H₂, C₂H₄ and CH₃ were measured in a HF activated 0.5% CH₄ in H₂ gas mixture at 25 Torr.  Acetylene, being the most stable hydrocarbon at lower reactor temperatures (i.e. far from the filament), was shown to be the most abundant gas-phase species, while concentrations of other stable hydrocarbons, such as C₂H₆, C₃H₄ and C₃H₈, were below the detection limit.

 

Using the highly sensitive laser-based absorption technique Cavity Ring Down spectroscopy (CRDS), described in Appendix 3, Zare et al.[73] studied the absolute number density of CH₃ radicals in the gas-phase environment.  Their results indicated a peak in CH₃ number density ~4 mm from the filament surface.  The significance and validity of this result is discussed further in Chapter 3, together with comparisons of REMPI measurements obtained at Bristol.

 

These studies have been backed up by theoretical simulation studies of the gas-phase environment and the growing surface[74].  Without doubt, the HF CVD system is the most studied of the diamond deposition techniques.  The need for a greater understanding of the gas-phase environment, gas-surface interactions and the growth scheme remains in order to increase understanding of the process and optimise deposition process conditions.

 

It is the ability to scale-up the HF process that encourages its use in the diamond tool coating industry.  The need to coat three dimensional tool edges and inserts requires a dynamic system such as provided by HF CVD.

 

 

1.8.2   Microwave-plasma assisted CVD system

 

In a microwave-plasma assisted CVD (MPACVD) system, as the name suggests, microwave radiation (typically 2.45 GHz) is coupled into the gas mixture thereby forming and sustaining a plasma.  Electron bombardment is a significant contributor to ionisation and decomposition of the gas.  Efficient coupling of energy into vibrational levels allows gas temperatures of 2000-3000 K to be attained, prompting thermal dissociation of molecular hydrogen.  As in HF CVD, atomic hydrogen initiates the necessary gas-phase chemistry.  Figure 1.12 schematically outlines the main parts of a MPACVD system.

 

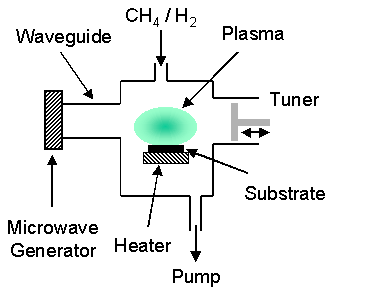
Figure 1.12  Schematic outlining the major components of a typical MPACVD system

 

While the gas composition, pressure, and obtained growth rates are similar to that of a HF system, microwave systems have the advantage of being able to produce large diameter films.  Since no electrodes or filaments are used to decompose the gas mixture, the films grown are not contaminated by metal impurities.  This has led to studies into the growth of MPACVD doped diamond films to exploit their electronic properties[75].

 

The substrate is usually positioned so as to make contact with the visible plasma ‘ball’.  Diffusion is thought to be the major transport mechanism by which active species reach the substrate.  Bias-enhanced nucleation (BEN), whereby a potential is applied to the substrate in order to enhance the nucleation stage, is commonly used in MPACVD systems[76].  The BEN effect occurs due to the presence of charged species produced in the plasma.

 

Since MPACVD systems are not reliant on filaments or electrodes (which may deteriorate in oxidising gas mixtures) to activate the gas-phase chemistry, a wider range of input gases have been studied from the viewpoint of diamond deposition[77].  Of these, studies of oxygen addition in particular have led to an increase in knowledge of the gas-phase chemistry involved, as summarised in chapter 1.5.4.

 

 

1.8.3   Oxyacetylene Torch CVD

 

One way of producing a sufficient number of active species for diamond deposition is via the highly exothermic reactions that occur in flames.  The Oxyacetylene torch CVD method, shown schematically in figure 1.13, burns a mixture of C₂H₂ and O₂ to produce a high enthalpy flame.

 

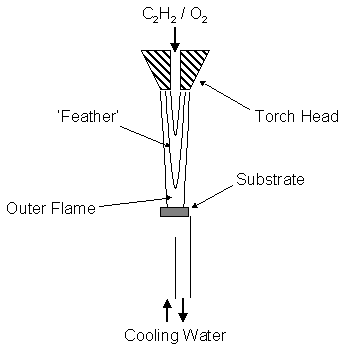
Figure 1.13  Schematic of a typical oxyacetylene diamond CVD system

 

The high velocity flame impinges onto a water-cooled substrate and has been shown to deposit high quality diamond[78].  The acetylene is oxidised to produce carbon monoxide and atomic hydrogen in a highly exothermic reaction (DH_reac ~ -448 kJ mol^-1), resulting in flame temperatures in excess of 3000 K.  Carbon monoxide is stable at such high temperatures and any unreacted acetylene may be converted into hydrocarbon radicals via reaction with atomic hydrogen.  For this reason, diamond deposition is typically carried out with an acetylene flow marginally greater than that of oxygen.  This in effect produces an optimum hydrocarbon radical concentration within a region of the flame known as the ‘acetylene feather’.  Diamond deposition is carried out onto a substrate positioned within this region.

 

Growth studies have demonstrated the deposition of polycrystalline diamond at growth rates approaching 200 mm hr^-1.  Films deposited by this technique suffer from non-uniform radial growth, reflecting the radial variation in flame composition and substrate temperature.  Attempts to overcome this problem via nozzle modifications and turbulent–flame techniques have so far shown only minimal improvements[79].  The introduction of flat-flame burners has been shown to enable uniform deposition over areas up to 13 cm² and such burners have started to replace the more typical welding torch design[80].

 

Extensive studies using Laser Induced Fluorescence (LIF) have been carried out focusing on radial distributions of C₂, CH, OH and CN within the flame[81].  While the gas-phase chemistry is very different from that in typical methane-hydrogen CVD environments, the actual growth mechanism is thought to be the same.

 

Since this technique is relatively inexpensive to set-up and, in terms of deposition, extremely flexible, its use has been postulated for thick film coating of objects that have niches or curved surfaces[82].  Unlike all other deposition techniques, oxyacetylene torch CVD may be carried out at atmospheric pressure without the use of vacuum equipment.  This has obvious advantages over HF and microwave CVD coating methods.

 

 

1.8.4   Plasma-jet CVD system

 

The term Plasma-jet refers to a medium to high pressure CVD system whereby convection is the main transport mechanism, energy may be provided by a number of means.  Radio-frequency (RF) inductively coupled plasma jets and microwave plasma assisted plasma jets have both been shown[83] to deposit high quality diamond films.  In general, direct-current (DC) plasma jets are most commonly used.

 

Figure 1.14 shows a schematic illustration of a typical DC plasma jet system used for diamond deposition.  DC plasma jets (also known as DC-arcjets) operate by passing an electric arc discharge through a gas flow, which via ohmic heating increases the gas enthalpy and kinetic energy, thereby producing a plasma jet (plume).  For diamond deposition, the plasma jet system typically operates on an Ar/H₂/CH₄ gas mixture, with the hydrocarbon usually being added downstream of the torch head to prevent the deposition of amorphous carbon on the exit nozzle.  The plasma jet expands into a reaction chamber maintained at a medium to high pressure and impinges onto a water-cooled substrate typically maintained between 1000–1500 K.

 

 

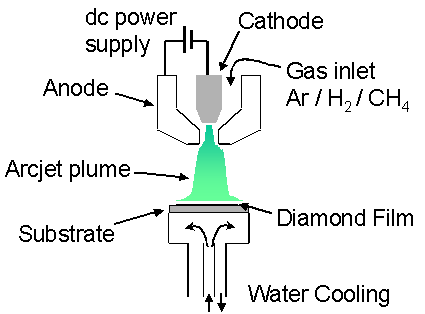
Figure 1.14  Schematic outlining the major components of a diamond depositing DC-arcjet CVD system.  Adapted from reference [84].

 

The expansion of the plasma jet is thought to be supersonic in some systems[85] with the plume velocity being dependant on both the design of the torch head and the pressure difference between the torch head and the main chamber into which the plume expands.  As the plume expands into the main chamber the pressure difference promotes the gas dynamic conversion of thermal energy into kinetic energy to form the plume.  The high convection velocity of species within such a system is thought to account for the high growth rates obtained.

 

Since convection dominates the species transport the residence time within the reactor is strictly defined.  This provides a significant conceptual advantage when modelling plasma jet systems, as compared with other CVD methods in which diffusion is the primary species transport mechanism and therefore the residence time is less clearly defined.

 

The high average gas temperature within the plume exceeds that obtained via thermal activation methods as used in HF CVD.  As a result of the high gas temperatures the decomposition of molecular hydrogen to form atomic hydrogen, a species fundamental to diamond deposition, is more complete.

 

Since the first demonstration of DC-arcjet diamond deposition by Kurihara et al.[86] published in 1988, a number of groups have endeavoured to optimise process conditions, determine growth characteristics and lower film production costs.  In 1990 Ohtake et al. demonstrated what remains the highest reported linear growth rate from a gas precursor using any CVD technique by using a DC plasma jet system[87].  The study achieved a growth rate of over 900 mm hr^-1 with a carbon conversion efficiency of approximately 8%.  However, by using a hydrocarbon liquid precursor injected through the substrate even higher growth rates of ~1mm hr^-1 have been demonstrated[88].

 

A range of other techniques have been shown to further improve both the rate and quality of film deposition.  For example, by using a secondary discharge, positioned above the substrate, an increase in both film quality and growth rate is achieved[89].  It is thought that the secondary discharge maintains an increased atomic hydrogen concentration above the substrate, hence counteracting its recombination in the boundary-layer.

 

Growth rates from the reported studies are extremely varied; this may be clarified when the large differences in input power are taken into consideration.  The growth rate has been shown to scale with the input power used[90].  Surprisingly, the content of non-diamond (or the defect density) was also found to increase as a function of input power.  The study concluded that the increase in input power increased the concentration of atomic hydrogen, which is consequently consumed in activating hydrocarbon radicals, leading to an enhanced C:H ratio (in excess of the optimal value), thereby causing an increase both in the growth rate and the defect incorporation in the growing film.

 

The number of gas-phase studies of plasma jets during diamond deposition is considerably less than for the more common CVD systems, but significant progress has nonetheless been made using a number of diagnostic techniques.

 

Kawarada et al.[91] used optical emission spectroscopy (OES), described in appendix 4, to ascertain some of the species present within the plume.  OES is restricted to detection of emitting species only and is subject to collisional quenching, for these reasons it is difficult to determine reliable species concentrations solely from emission data.  Another OES study by Loh and Cappelli[92] concluded that the high diamond growth rate is due to high gas flow rates and rapid quenching of the plasma at the substrate.  Rapid quenching of the high temperature plasma (>5000 K) was thought to produce super-equilibrium levels of hydrocarbon radicals.

 

Using both LIF and OES to ascertain plasma temperatures, Gicquel et al.[93] were able to refine a gas-phase model, thus providing one of the earliest and most fundamental studies of DC plasma jet diamond deposition.  The group incorporated a stagnation boundary layer at the substrate into their hydrodynamic model and, in conjunction with diagnostic measurements, found the plasma temperature to fall linearly from a maximum of 5000 K to 2100 K at the stagnation boundary in front of the substrate and to 1200 K at the substrate surface.

 

Plasma diagnostics found the electron and gas temperatures to be almost identical, leading to the conclusion that the plasma was essentially thermalised.  By utilising the hydrodynamic model, an atomic H mole fraction of 0.460 was calculated at the boundary layer, indicating that approximately 25% of the feedstock H₂ dissociates.  Once produced, atomic hydrogen and carbon both persist in the plasma since consumption of these species involves a three-body reaction (from inspection of data in reference 25).  Given the high atomic H concentrations in the plasma, it is unlikely that methyl radicals persist long enough in the gas-phase to propagate to the substrate at high enough concentrations to account for observed growth rates of over

100 mm hr^-1.  In their study the group therefore suggested that atomic carbon might play a role in diamond growth, with the majority of the total carbon balance being converted into polyatomic hydrocarbon species in the cooler regions peripheral to the plasma.

 

Further evidence of the plasma being close to thermalised in a low-pressure (20 Torr) regime was revealed by findings that the electron temperature was only a factor of two greater than the gas temperature[94].  Larger discrepancies in the electron and gas temperatures are commonly seen at higher pressures.  One other aspect of this study also identified a plateau in the gas temperature with increasing input power, an observation attributed to the absorption of energy by the reaction, H₂ ® 2H.

 

Modelling the SRI reactor using an experimentally determined temperature profile, together with gas-phase chemistry, stagnation flow hydrodynamics and diamond surface chemistry, Goodwin was able to calculate the atomic hydrogen concentration as a function of position, including close to the substrate surface[95].  At a distance of 0.2 mm from the substrate surface the atomic hydrogen mole fraction was calculated to be approximately 0.2, corresponding to about 11% dissociation of the molecular hydrogen feed.  In contrast to earlier studies, Goodwin was able to show that calculated CH₃ concentrations (~2.0´10^-4 mole fraction) were sufficiently high to account for the observed high growth rates in DC plasma jet CVD.  Atomic carbon concentrations were shown to be about a factor of 10 higher than that of methyl radicals in the gas-phase close to the substrate.

 

While these reports are informative, and go some way to providing an initial insight into the gas-phase chemistry involved in the diamond depositing DC plasma jet system, it is worth noting that the early reactor designs are fundamentally different to the modern reactor.  The realisation that remote addition of the hydrocarbon downstream from the torch head both improves the deposition rate and prevents the build up of amorphous carbon within the torch head, has promoted the use of remote hydrocarbon addition.  Improvements in modelling carried out by Dandy and Coltrin[96] took into account gas-surface chemistry, and the effect of a swirling gas flow upon stagnation flow hydrodynamics.  One of the conclusions from this influential study was the identification of two diamond growth regimes, which it was suggested, are dependant on the degree of H₂ dissociation in the gas phase.  For schemes where H₂ dissociation is low (~5%), CH₃ is thought to be the dominant growth species, whereas in the event of high H₂ dissociation (up to 95%), it was postulated that atomic carbon is the dominant growth species, with the growth rate increasing with the extent of H₂ dissociation.

 

While any reported model will be tailored to a specific reactor and deposition conditions a number of general trends have emerged.  In a combined diagnostic and modelling study Reeve et al.[97] identified a number of similarities in the trends of gas-phase species concentrations in previously published work.  By using the CHEMKIN gas-phase chemistry modelling package²⁴ the group calculated the CH₃ radical concentrations near the nozzle of the torch head.  They found CH₃ to be the dominant hydrocarbon within 5 cm of the nozzle implying that this region corresponded to the low H₂ dissociation regime.  Further from the nozzle exit, further H atom abstraction occurs, leading to formation of other hydrocarbon species.  As the Reeve et al. group typically deposit diamond onto a substrate positioned, at most, 5 cm from the torch head nozzle, their study goes some way to underline the role of methyl radicals in diamond growth in this plasma jet environment.

 

Reeve et al. have also postulated that systems using remote hydrocarbon addition, being subject to inefficient mixing of the hydrocarbon with the plasma, may in effect lower the residence time of active species in the hot plume.  Typically CH₄ is used as the input hydrocarbon which, via H atom abstraction, forms CH₃.  The CH₃ radical may in turn suffer H atom abstraction (as shown in figure 1.4).  It was suggested that the residence time might be sufficiently reduced by using a remote hydrocarbon addition system and so maximise CH₃ production.  Loh and Cappelli[98] also attempted to study the effect of reducing the species residence time by increasing the gas flow rates (in a study involving CH₄ addition through the torch head).

 

Thus it is clear that, in order to optimise diamond deposition from CH₃, a low residence time is required to minimise further abstraction reactions.  This would be easier to prove if it were possible to quench the hydrocarbon chemistry by reducing the available atomic hydrogen.  However, H atoms at the substrate surface are vital for high quality diamond growth.  Therefore, an optimum H₂ dissociation level must exist within this regime for a given species residence time, so as to achieve the necessary compromise between maximising CH₃ concentrations, while maintaining sufficient H atom flux at the substrate.

 

Mass spectrometry has been used to monitor the exhaust gases from a diamond depositing DC plasma jet reactor, the major stable reaction products being CH₄, C₂H₂ and C₂H₆ [99].  Little information of the gas-phase chemistry involved in diamond deposition may be gained via mass spectrometric analysis of the exhaust gases, the hot plume preventing any in-situ sampling.

 

Electrostatic probe analysis has been used to ascertain the electron temperature and densities within a diamond-depositing plume⁹⁶.  Reeve and Weimer used a floating double probe technique, yielding respectively, electron temperatures and electron densities of 2.3 eV and 7´10¹¹ cm^-3 near the nozzle exit and 0.4 eV and 1´10⁹ cm^-3 downstream.  This study shows the plasma to be weakly ionised concluding that reactions involving electrons must only play a minor role in diamond deposition.  The DC plasma jet in this study was generated by a 2.8 kW discharge with expansion into a chamber maintained at 60 Torr.  This study represents a low-power system and while both the electron temperature and density in the plume will increase with increasing input power, it is still thought that reactions involving electrons are not essential to diamond deposition.

 

By using a Langmuir probe, Stalder and Jefferies[100] measured the electron temperature (T_e) and density as a function of process gas composition in a

1-2 kW discharge plume expanding into a chamber maintained at 25 Torr.  Collisionless thin-sheath probe theory was used to interpret the I-V curves obtained.  In the high velocity plasma jet the mean free path will be significantly greater than the Debye length, validating the use of collisionless theory.  This study showed very little variation in T_e as a function of distance from the nozzle exit.  The group also measured the ion density and T_e to be respectively 6x10¹¹ cm^-3 and 1.1 eV at a distance of 13 mm from the nozzle exit operating on a diamond depositing gas mixture (49% H₂ / 51% Ar / 0.2% CH₄).

 

Furthermore, the group found that the electronic properties of the plasma deviated from that predicted by the Saha equation, with the electron density being more than six orders of magnitude greater than that calculated.  The Saha equation, described in detail in Appendix 5, relates the electron density to the ionisation potential and electron temperature, assuming Boltzmann equilibrium applies to both the neutral and ionised species of the plasma.  The deviation in the value from that predicted using the Saha equation signifies non-equilibrium between the electron-ion density and the gas and electron temperatures.  In order to produce such a non-equilibrium situation it was concluded that, while species ionisation is primarily carried out in the activating arc, the resulting free electrons are transported downstream via convection.

 

Brinkman et al.¹⁰³ have drawn comparisons between species emission and ion densities within the plume.  By studying the emission intensity and ion density as a function of distance from the nozzle exit, it was shown that the CH and H (Balmer-g) emission falls by a factor of 25 to 30 from 13 to 42 mm downstream of the nozzle exit, while the ion density drops by a factor of 10.  The emission from the C₂(d) state measured over the same range showed a smaller decrease, approximately a factor of three.  It was concluded that while emission from H and CH is by means of electron impact excitation, C₂ emission must arise by another means.  It has been postulated therefore that chemiluminescent reactions account for most of the C₂ emission.

 

Storm and Cappelli[101] have carried out similar studies finding electron densities of approximately 10¹³ cm^-3 in a 1.4 kW hydrogen arcjet.  While this level of ionisation is about ten times higher than that measured by Brinkman et al., it is thought to be consistent with a decrease in ion density with axial distance.

 

In the study of diamond depositing DC plasma jets, OES is the most commonly used diagnostic tool.  This non-invasive spectroscopic technique has been used to analyse the composition of the high luminescent plume by a large number of groups [102]^,[103].  OES relies on the collection of spontaneous emission from a species in an excited state.  The experimental set-up of each OES study is fundamentally the same.  Emission is collected along an axis at right angles to the plasma flow, defined into a column, and conveyed by a fibre optic into a spectrometer.  Wavelength dispersed emission is collected via a charge-coupled device (CCD) array or a photomultiplier tube positioned at the exit of the spectrometer.  Within the visible wavelength range

350-700 nm, emissions from the species C₂, CH, H, C, Ar and, where applicable, CN and CO are detectable.  This has led to studies measuring the emission intensity of these species as a function of process conditions, in order to ascertain rotational temperatures and species trends.  However, quantitative species analysis is complicated by collisional quenching and species self-absorption within the plume.

 

OES studies performed by Reeve, Weimer and Cerio[104] concentrated on the rotational and vibrational excitation temperatures of C₂ and CH.  Spatially resolved emission spectra were taken to ascertain species temperatures in a plane between the nozzle exit and the substrate.  Plasma excitation temperatures were determined by fitting calculated optical emission spectra associated with the d³P_g ® a³P_u transitions of C₂ and the A²D®X²P transitions of CH to measured spectra.  Only a scaling factor, the vibrational temperature (T_vib) and the rotational temperature (T_rot) were used as fitting parameters in a least-squares fit of the observed and calculated spectra.  To derive a meaningful temperature from an emission spectrum the emitting species must be thermalised.

 

As deviation from thermodynamic equilibrium is common in reacting plasmas, small differences between electronic, vibrational and rotational temperatures and the gas temperature are expected.  Any differences in these temperatures from the optical emission are directly linked to the excitation and de-excitation processes that produce non-equilibrated excited state populations.  The competing de-excitation processes include spontaneous emission, rotational and vibrational energy transfer and collisional quenching.  Results of the fitting procedure showed a good agreement between the C₂ and CH observed and calculated spectra.

 

Determinations of the T_rot and T_vib showed that while the plasma is not thermalised i.e. T_rot ¹T_vib, a general temperature trend existed as a function of distance from the substrate.  Reeve et al. thus concluded that excited state C₂ and CH are likely to be strongly quenched by H₂.  They also concluded that the excitation mechanism for C₂ and CH are very different, resulting in widely different rotational and vibrational excitation temperatures.

 

It is thought that in the bulk plasma, chemiluminescent reactions are responsible for producing CH emission, while rotational and vibrational temperatures, determined from optical emission spectra, indicated that C₂ excitation occurs via electron impact.  Close to the substrate, it was thought that thermal excitation is most likely to be the major excitation mechanism for both CH and C_2, as the plasma closely resembles a hot neutral gas.

 

In a study carried out by Cubertafon et al.[105] emission spectroscopy was used to produce rotational temperature maps of the plume.  Spatially resolved rotational temperatures of the CH (B²S®X²P) band revealed a relative plateau in the temperature profile from the nozzle exit, where

T_rot ~2600 ± 200 K, to a point approximately 5 mm from the substrate surface where the temperature drops rapidly towards the substrate temperature (~1200 K).  This trend has been substantiated by a pulsed laser Rayleigh scattering study[106].  Emission from atomic carbon (3s:¹P®2p²:¹D and 3s:¹P®2p²:¹S) was shown to be stable throughout the distance from the nozzle exit to close to the substrate surface where it decreased.  Cubertafon et al. hypothesized that atomic carbon is therefore consumed at the growing surface as a precursor to diamond growth.  This finding is consistent with a number of models which identify atomic carbon as a growth species[107]^,[108].

 

Results of measuring the electron density from the Stark broadening of the H Balmer lines have also been reported.  Due to the large electron flux within the plasma jet, Stark broadening of emission lines is observed and may be used to estimate the local electron density¹¹⁰.  H Balmer-a emission was collected and fitted in terms of a Voigt profile with a Gaussian contribution removed to allow for instrument broadening.  The resultant broadening of the emission line was shown to be strongly dependent on the torch anode-cathode separation.  Electron densities, obtained from the FWHM (Full-Width Half Maximum) of the Voigt profiles, are estimated to be in the region of

10¹⁵-10¹⁶ cm^-3 close to the nozzle exit of a torch operating between 3-5 kW on an Ar/H₂/CH₄ gas mixture.

 

While no data were published, it was stated that the electron density falls as a function of distance from the nozzle exit.  The report notes, that while the line broadening (and hence electron density) is influenced by the anode-cathode separation, the quality and growth rate of the films are not.  This provides further evidence that the precise value of the electron density plays a minor role in determining the gas-phase environment prior to diamond deposition.

 

Attempts have been made to estimate the electron temperature from the relative emission intensities of the atomic hydrogen Balmer series[109].  The method used by Luque et al. assumes the excited states of atomic hydrogen have similar electron impact excitation cross-sections and collisional quenching rates.  The emission intensity is then related to the electron temperature via equation 1.2,

 

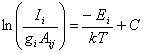                            Equation 1.2

 

where I_i is the emission intensity from level i, g_i is the degeneracy of this level, A is the Einstein A coefficient for the i®j transition, E_i is the energy, k the Boltzmann constant, T the electron temperature and C is a constant.  In previous studies[110] it was found that the departure from thermodynamic equilibrium deems this technique unreliable.

 

By using Laser-Induced Fluorescence (LIF) techniques, discussed in Appendix 2, absolute number densities for a series of species have been estimated[111]^,[112].  By probing the ground (or low-lying excited) state, LIF has the advantage over OES of providing absolute species number densities unaffected by deviations in thermal equilibrium.  Luque et al. have used LIF to determine spatial distributions of C₂, C₃ and CH.  It was shown that C₂ and CH both have a maximum radial number density in the centre of the plume, while C₃ is concentrated in a hollow cylinder about the jet axis.  As previously shown by OES, CH number density was found to maximise about 1 mm from the substrate.

 

Rotational and vibrational temperatures of the detected species were also measured and compared with a rotational temperature gained from NO, a non-reacting species.  Differences of ± 200 K were found in the free stream of the plume for CH rotational and vibrational temperatures and the rotational temperature of NO.  Within the axial centre of the plume a local gas temperature of 2300 ± 150 K was obtained.  Comparisons between optical emission-based measurements and LIF measurements of temperature have been drawn[113].

 

OES measurements from rotational and vibrational excited CH and C₂ radicals yielded temperatures in the range 3000-7000 K, whereas LIF measurements of the vibrational and rotational state populations in the respective electronic ground states, gave temperatures in the 1200-2200 K range.  These discrepancies merely serve to underline the problems associated with the non-equilibrium nature of the plasma, and some of the difficulties in interpreting plasma properties from the optical emission.

 

It is worth noting that while a number of general trends exist in both the gas-phase and surface chemistries, as well as the hydrodynamic properties within DC plasma jets, each diagnostic measurement and model calculation will be specific to the reactor used.  Contributions to any difference in observed parameters may come from torch head and reactor design, together with deposition conditions such as input power, input gas mixture, etc.

 

DC plasma jets have an advantage over other CVD techniques in that the deposition of diamond can proceed simultaneously with the deposition of ceramics and metals.  Kurihara et al.[114] deposited a 40 mm thick diamond film onto a tungsten-molybdenum substrate, by depositing a preliminary layer of tungsten carbide followed by a diamond-tungsten carbide layer.  Such graded material reduced the thermal stress between the diamond film and the substrate, and increased the overall film adhesion strength by an order of magnitude.

 

Commercially, the use of a DC plasma jet system to deposit diamond has not proven to be as successful as other techniques.  The initial cost of a DC plasma jet system is considerably higher than competitive microwave and hot filament reactors.  Since plasma jets require the consumption of large quantities of both power and process gases (argon and hydrogen) it is not thought currently to be economically viable except for the production of small diameter thick freestanding films.  Recent studies by a Chinese group have shown how gas recycling may lower the film production costs[115].  These studies demonstrated a recycling efficiency of 85%, with a concomitant reduction in diamond production costs from approximately $45 to $21 per carat.

 

Regardless of the economic drawbacks of DC plasma jet deposition, the unsurpassed growth rate and high quality deposition explains why plasma jets continue to attract interest as a deposition technique.

 

 

References