Chapter 3 : REMPI studies of H atoms and CH3 radical species
in a HF-CVD reactor
This chapter
contains the results of REMPI studies of H atom and CH3 radical
species in a hot filament CVD reactor, with the addition of CH4 or C2H2
to a H2 gas flow. Experimental
considerations were discussed in chapter 2.
The gas-phase
chemistry of H2 and CH4 input mixtures have been
previously studied in some detail[1]
with H atoms and CH3 radicals being widely recognised as
fundamentally important species in the hot filament diamond CVD environment.
H atom
(ground-state) detection in a diamond CVD environment has been carried out
previously using direct absorption on the n = 2 ¬ n = 1
Lyman-a transition[2],
LIF monitoring of the n = 3 ® n = 2 Balmer-a emission following n = 3 ¬ n = 1
two photon excitation[3],
3+1 REMPI[4]
and in-situ third harmonic generation
(THG)[5]. The experimental studies described in this
chapter concentrate on 2+1 REMPI of both H atoms and CH3 radicals,
the use and validity of which has been previous outlined in chapter 2.
3.1
H atom detection
For
simplicity, the initial studies described here were carried out in a pure H2
gas phase environment rather than the dilute hydrocarbon / hydrogen gas mixture
used in diamond deposition.
2+1 REMPI was
used to detect H atoms, via the collection of H+ ions. As discussed in chapter 2, the Doppler
broadened H atom lineshapes may be used to assess the relative H atom number
density and the local gas temperature.
Spatially resolved measurements of the H atom distribution and local gas
temperature were made as a function of distance from the hot filament surface,
in a chamber containing 100% H2 at 20 Torr. Figure 3.1a shows the trend in local gas
temperature (Tgas),
acquired from the Doppler broadening of the H atom lineshapes, as a function of
distance from the filament surface, d,
with a constant filament temperature of 2375 K.
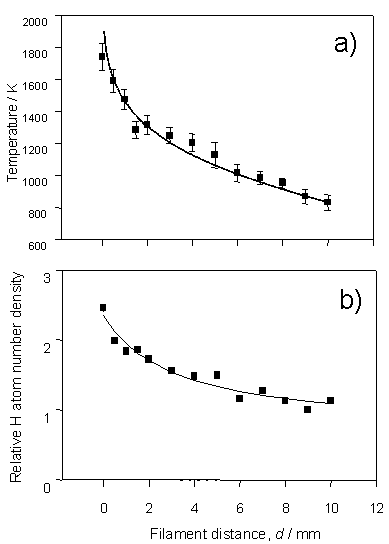
Figure 3.1 H atom lineshapes
yield a) local temperature dependence and b) relative H atom number density,
both shown as a function of distance from the filament surface. The data were recorded by monitoring the H
atom 2s ¬ 1s two-photon
transition using a chamber containing 20 Torr H2 at a flow rate of
100 sccm and a filament temperature, Tfil,
of 2375 K.
The solid
curve in figure 3.1a is obtained using equation 3.1, which has been used to
describe the radial temperature distribution in computational models[6].
Td = Td=0{1-[1-(TL/Td=0)2]ln((d + Rf)/Rf)/ln(L/Rf)}0.5 Equation 3.1
Td=0 and TL
in this equation are the gas temperatures in the immediate vicinity of, and at
a distance L from, the hot filament
surface. The filament radius, Rf, is 125 mm (the
diameter of the tantalum filament). The
correlation between the calculated temperature profile and that obtained
experimentally serves to validate the local gas temperature determinations from
the H atom Doppler profiles.
Figure 3.1b
shows the trend in relative H atom number density, also written as [H], as a
function of distance from the filament surface. Similar radial [H] profiles have been derived using Vacuum
Ultraviolet (VUV) absorption[7],
LIF3 and THG probing[8],
in hot filament systems. The peak in
[H] at the filament surface reinforces the claim that atomic hydrogen is formed
on the surface of the hot filament, by thermal dissociation of H2,
and diffuses into the bulk gas. The
recombination rate of H atoms at typical chamber pressures and temperatures is
sufficiently slow that [H] in the bulk gas is greatly in excess of that
predicted on the basis of equilibrium thermodynamics.
It has previously
been shown that no discernable change in [H] or Tgas is detected when operating on an identical set-up
with a total H2 flow rate of
50 sccm[9]. This supports the assertion that diffusion
is the principle transport mechanism in a hot filament reactor.
Once the use
of REMPI has been justified in the study of relative H atom number densities,
the [H] may be monitored as a function of process conditions. By using REMPI, [H] was found to be
essentially independent of the H2 pressure. This supports previous LIF studies[10]
and measurements of the pressure dependence as a function of filament power
consumption[11], concluding
that, at typical gas pressures and temperatures, H atoms are produced as a
result of H2 bond fission on the surface of the filament. The production of atomic hydrogen on the
filament surface represents a mechanism whereby the kinetics are zero-order,
with respect to the H2 pressure.
With the increase to higher H2 pressures a gradual fall in
[H] is observed and attributed to the three-body homogenous recombination
reaction,
H +
H + M(H2) ® H2 + M(H2) Reaction 3.1
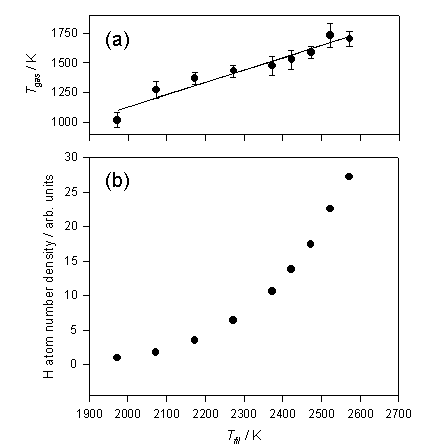
Figure
3.2 shows the trends in Tgas
and [H] as a function of filament temperature.
Figure 3.2 a) Tgas and b) relative H atom
number densities deduced from analysis of the H atom Doppler lineshapes
measured at d = 1 mm, measured as a function of filament temperature (Tfil).
Tgas scales relatively linear with Tfil, however, even at 1 mm from the filament surface
the gas is ~700 K cooler than the filament surface. Early studies by Langmuir[12]
also documented similar large temperature drops near the filament surface. Relative H atom number densities appear to
increase exponentially within the filament temperature range measured. Plotting ln[H] against 1/Tfil (a Van’t Hoff type plot)
yields a straight line, the gradient of which may be interpreted in terms of -DHDISS/R, where DHDISS has the value
240 ± 20 kJ mol-1
and is the deduced enthalpy for forming a mole of H atoms on the surface of the
filament. The surface mediated H atom
formation scheme is outlined in the reversible reactions 3.2 and 3.3.
H2 + S* ¾ H + SH Reaction 3.2
SH ¾ H + S* Reaction
3.3
These
reactions describe the dissociative adsorption of H2 on an active
filament surface site (S*) and H atom recombination on a hydrogen-terminated
filament surface (Reaction 3.2 forward and reverse). The reversible reaction 3.3 describes the desorption and
absorption of atomic hydrogen onto the filament surface. Changes in Tfil will influence the H atom filament production rate
by affecting the mean lifetime of chemisorbed species on the filament surface,
together with its energetic influence on the H atom formation reaction
scheme. The temperature of the filament
also affects the fraction of available S* and the local gas phase H atom number
density which, in turn, influences the fraction of active sites via the reverse
of reaction 3.3. Overall the filament
acts as a means of providing active sites and a medium by which H2
molecules may attain Tfil. In terms of a reaction scheme, the overall
total reaction facilitated by the hot filament surface (i.e. the sum of
reactions 3.2 and 3.3), is simply,
H2 ¾ 2H. Reaction
3.4
The addition
of a dilute hydrocarbon to the pure H2 environment complicates
matters, since, as described earlier in section 2.4, the filament surface
becomes carburised and thus changes the number and type of available sites at
the filament surface.
Previous H
atom REMPI studies have shown that the addition of small quantities of methane
causes a reduction of [H] for a given Tfil. This may be considered consistent with the
presumed change in the filament surface and a reduction in the fraction of
active sites. The loss of H atoms in
the gas-phase may also be explained by analysis of the gas-phase reactions that
are occurring. Abstraction reactions,
similar to that shown in reaction 3.5, provide a gas phase loss mechanism for H
atoms together with a route by which methyl radicals are produced.
H + CH4 ¾ H2 + CH3 Reaction 3.5
3.2
Methyl Radical detection
The detection
of methyl radicals in a diamond-depositing reactor via 2+1 REMPI has been
previously explored[13],
for the purposes of these studies the origin band of the 
transition was investigated. Figure 3.3 shows a power normalised spectrum
of the 
origin band transition of CH3,
recorded using a 1% CH4 / H2 gas mixture with Tfil = 2475 K, probing at d = 4 mm.
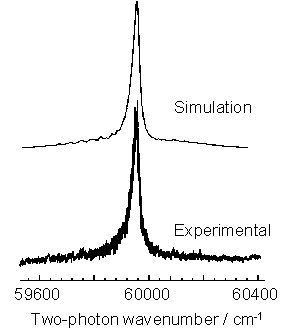
Figure 3.3 2+1 REMPI spectrum
of the CH3 (
) transition (lower trace)
with a best-fit simulation of the origin band contour (upper trace).
The Q branch
dominates the spectrum with weak underlying contributions from O, P, R and S
branch structures producing an underlying pedestal.
The simulation
shown in figure 3.3 (upper trace) was produced with prior knowledge of the
ground and excited state spectroscopic parameters (listed in table 3.1), the
nature of the excited state predissociation and the two-photon rotational
linestrengths.
The rotational
constants, detailed in table 3.1, define the rotational transitions for the
oblate symmetric rotor CH3 radical.
For such a structure, the ground and excited state respective rotational
values are given by,
Equation 3.2
The full width
half maximum of a line to a given excited state N,
is given by,
, Equation
3.3
where w is a
linestrength factor which determines the relative weights of the zero rank
(scalar) and second rank tensor components of the two photon transition
probability.
The only
variable parameter is the rotational temperature which, in the case shown, is
identified as 1150 K. This is in
agreement with the local gas temperature gained via H atom Doppler analysis for
equivalent conditions and serves to highlight that local thermodynamic
equilibrium (LTE) exists in this type of CVD reactor. With an estimated collision frequency of ~108
s-1, for typical gas pressures and temperatures reached in HF-CVD
reactors, the rotational temperature exhibited by CH3 radicals is
equal to the gas temperature denoted by H atom Doppler lineshape analysis, and
thus LTE exists.
|
Constant |
|
|
Units |
|
n0 |
59955(5) |
|
cm-1 |
|
B0 |
9.51(7) |
9.57789 |
cm-1 |
|
C0 |
4.62(3) |
4.74202 |
cm-1 |
|
DJ |
7.7 |
7.699 |
10-4
cm-1 |
|
DJK |
-13.6 |
-13.58 |
10-4
cm-1 |
|
DK |
6.3 |
6.34 |
10-4
cm-1 |
|
v0 |
12(1) |
|
cm-1 |
W |
2.5(1) |
|
|
|
a |
0.05(2) |
|
|
|
b |
-1 |
|
|
Table 3.1 Molecular constants
of the CH3 
band used in the simulations. All constants taken from J. Heinze, N. Heberie and K.
Kohse-Hoinghaus, Chem. Phys. Lett.,
1994, 223, 305. except W, v0, and n0 which were derived from simulations of the measured spectrum.
Given that 2+1
REMPI is a viable means of monitoring relative CH3 number densities
[CH3], studies were conducted to ascertain [CH3] as a
function of process conditions and distance from the filament, d.
Rather than recording the entire band contour for each set of
conditions, the REMPI signal was collected at a single probe wavelength within
the transition. In order to convert the
CH3 REMPI signal into [CH3], the local gas temperature
needs to be known as a function of d
together with the application of a correction factor that recognises that both,
the population of the probed n = 0 level and
the origin band contour are temperature dependent. The local gas temperature profile, as a function of d,
is known from H atom Doppler lineshape analysis and is shown in figure 3.1a for
a given Tfil. The two temperature dependant correction
factors, by which the measured CH3 REMPI signal must be divided in
order to attain [CH3], are summarised in figure 3.4.
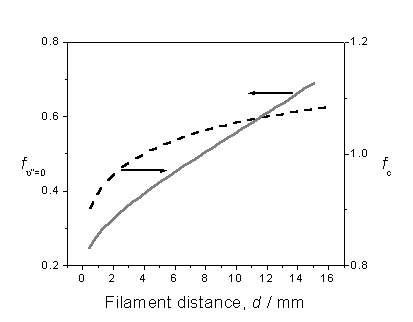
Figure 3.4 Plot illustrating the
variation in correction factors fc
and fn”=0 with filament
distance, assuming local gas temperatures provided by H atom Doppler lineshape
analysis.
Factor fc is obtained by calculating
the CH3 (
)
origin band contour for several different rotational temperatures, within the
range 600 – 1700 K, then determining the fraction of the total band contour
that falls within the bandwidth of the probe laser. The probe laser is assumed to have a Gaussian profile centred at
a two-photon energy of 59950 cm-1.
The other factor, fn”=0, recognises
that the REMPI probe wavelength only samples the fraction of methyl radicals
that are present in the ground vibrational state. Assuming that LTE exists, the temperature dependence of fn”=0 is calculated
given knowledge of the CH3 normal mode frequencies. The CH3 radical has two singly
degenerate fundamental modes, a symmetric stretch vibration
(n1 = 3004.4 cm-1)
and an out-of-plane bend (n2 = 606.5 cm-1),
together with two doubly degenerate modes, an asymmetric stretch (n3 = 3160.8 cm-1)
and an in-plane bend (n4 ~1400 cm-1).
The measured
REMPI signals will only provide a reliable measure of the total CH3
relative number density if the population in all of the populated vibrational
states is sampled with equal efficiency.
However, in the case of the CH3(
)
transition, the out-of-plane bending vibration (n2) participates
in the majority of the thermally populated levels with n” > 0. This, together with the Franck-Condon
requirement that Dn2 must be even,
ensures that all of the most significant hot band transitions in the 2+1 REMPI
spectrum of CH3 will be blue shifted with respect to the origin
band. Therefore, the measured CH3
REMPI signals must be corrected to reflect the trend in fn”=0.
The correction
factors were applied to CH3 REMPI signals collected from studies
focusing on [CH3] as a function of process conditions and filament
distance. Addition of trace quantities
of CH4 or C2H2 to a 100 sccm flow of H2
was studied in terms of CH3 production. Figure 3.5 shows the trend in [CH3] as a function of %
CH4 or C2H2 addition.
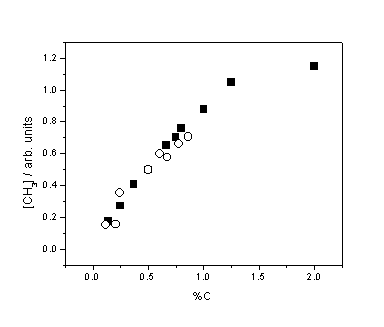
Figure 3.5 Relative CH3
number density as a function of %C from CH4 (¢) and C2H2 (™) addition. Measurements were
obtained with Tfil = 2475
K and d = 4 mm. The data points for the CH4 and C2H2
sets have been separately scaled vertically, in practice [CH3] is
approximately 2.5 times higher for CH4 than C2H2
for the same %C input.
The linear
trend in [CH3] at low CH4 addition (<2%) is in accord
with several previous measurements and is clearly different from the previously
identified constant [H] as a function of added H2. This reinforces the claim that methyl
radicals, unlike H atoms, are principally formed in the gas-phase and not on
the hot filament surface.
Monitoring the
CH3 REMPI signal, as a function of Tfil, reveals that in comparison to the H atom
dependence the CH3 REMPI signal rises less steeply. Figure 3.6 shows how both the H atom number
density and CH3 REMPI signal depend on Tfil.
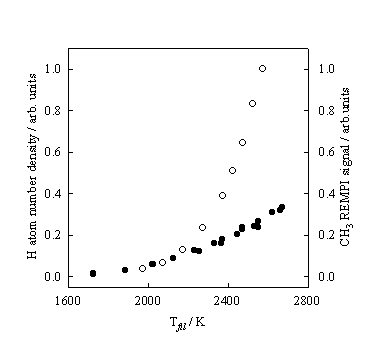
Figure 3.6 H atom number
densities (¡) and CH3 REMPI signal intensities (l) measured at, respectively, d
= 4 and 2 mm, and 20 Torr pressure, plotted as a function of Tfil.
The design of
the Hot-filament reactor and REMPI both allow spatially resolved number density
measurements to be undertaken. In this
case the filament was translated vertically, with respect to the laser focal
position and REMPI probe, to determine relative CH3 number densities
as a function of distance from the filament.
The collection
of spatially resolved H atom number densities has previously been discussed in
sub-section 2.3. Figure 3.7 shows the
radial dependence of the measured CH3 REMPI signal for a 1% CH4
in H2 gas mixture measured at a pressure of 20 Torr and Tfil = 2475 K. The plot shows how the measured signal (l) is
corrected, by inclusion of the correction factors fc and fn”=0 described
above, to form a relative number density measurement (¡).
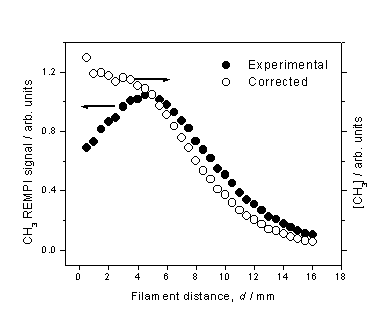
Figure 3.7 CH3 REMPI
signal (l) measured as a function of d
from a 1% CH4 in H2 gas mixture. The total CH3 relative number
density (¡) is obtained by scaling the measured REMPI signal by the temperature
dependent correction factors.
The peak in
measured CH3 REMPI signal is in accord with studies by Kruger, Zare et al.[14]
using cavity ring down spectroscopy (CRDS) to monitor a column of CH3
density in a hot filament reactor operating on a CH4/H2
gas mixture. We note, however, that
this peak becomes more of a plateau after correction for the temperature
dependant sampling efficiency. Nonetheless,
this observation is in marked contrast with the spatially resolved H atom
number density measurements, and may be explained by realisation that the CH3
number density is largely determined by the gas-phase equilibrium,
H + CH4 ¾ CH3 + H Reaction 3.6
Although the H
atom number density decreases monotonically with increasing d, the total gas number density (and
thus CH4 number density) increases.
This is due to the inverse dependence between number density and gas
temperature (for a constant pressure).
3.3 C2H2 gas-phase
chemistry
Previous
growth studies have demonstrated that the deposition of diamond may occur with
equal ability regardless of the hydrocarbon used[15]. Gas-phase simulations have been used to
study the species and reaction scheme.
A number of inconsistencies have been found, particularly in the
comparison of CH4 and C2H2 as hydrocarbon
sources1. Growth studies
have shown that growth by C2H2 occurs with similar
deposition characteristics (growth rate and quality) to growth from equivalent
carbon containing CH4 gas mixtures[16]. Close inspection of a C / H reaction scheme
(such as provided in GRI-Mech) reveals that there is not a viable route for the
production of CH3 radicals from C2H2 feedstock
gas at the elevated temperatures typically found in the CVD environment. This has led some to conclude that CH3
production from C2H2 must be facilitated by heterogeneous
conversion on the reactor walls, thereby providing a route to C-C bond breakage9.
With the
spatial resolution provided by REMPI and the reactor set-up, spatially resolved
CH3 REMPI signals, and hence, calculated number densities, were
obtained for a C2H2/H2 gas mixture. Obtaining the relative CH3 number
density as a function of d provides
an insight into the gas-phase chemistry, and serves to substantiate or
invalidate the conclusion that CH3 is formed via a gas-surface
reaction at the reactor walls. In the
experimental set-up the reactor walls are remote (>6 cm from filament) and
constantly cooled. Figure 3.8 shows the
measured CH3 REMPI signal obtained from a 0.5% C2H2
in H2 gas mixture as a function of d.
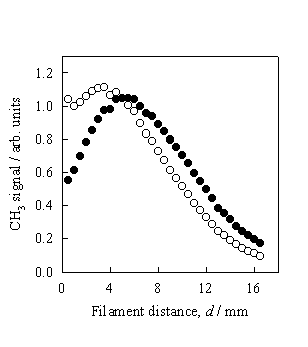
Figure 3.8 CH3 REMPI
signal (l) measured as a function of d
from a 0.5% C2H2 in H2 gas mixture. The total CH3 relative number
density (¡) is obtained by scaling the measured REMPI signal to the temperature
dependent correction factors.
The
measurements were taken at Tfil
= 2475 K and a chamber pressure of 20 Torr.
Clearly the trend shown in figure 3.8 is in close agreement to that
obtained using a 1% CH4 in H2 gas mixture (figure 3.7)
and serves to invalidate previous conclusions of CH3 production from
C2H2 via heterogeneous conversion.
Experimentally
determined CH3 number density variations with hydrocarbon/H2
mixing ratio, Tfil (Figure
3.9) and as a function of radial distance, all showed little sensitivity to
whether the carbon is introduced as CH4 or C2H2.
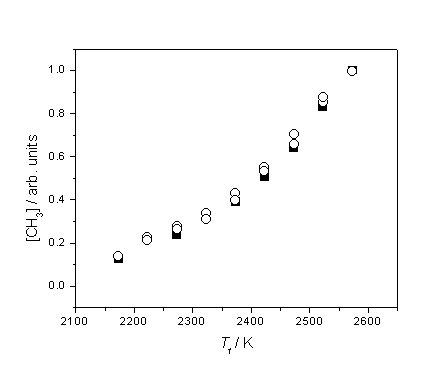
Figure 3.9 Plot highlighting
the similar trend of increasing [CH3] with Tfil using 1% CH4 in H2 (¢) and 0.5% C2H2 in H2 (™), probing at d = 4 mm.
The two datasets have been vertically re-scaled to coincide at Tfil = 2575 K.
Clearly the
two hydrocarbons must produce CH3 by different routes, but both must
be explained in terms of gas-phase chemistry.
Toyoda et al.2 have
argued that a sequence of H and H2 addition steps along the lines
of,
C2H2
+ H + M ¾ C2H3 + M Reaction 3.7
C2H4
+ H + M ¾ C2H5 + M Reaction 3.8
may provide a
gas-phase route to C-C bond cleavage.
Arguably the
most effective method to analyse the gas-phase chemistry, and to substantiate
experimental findings, is by comparison to a computer simulation. Working in collaboration with Moscow State
University, we were able to produce experimental data, the results of which
were analysed and compared to gas-phase computer simulations in Moscow.
3.4 Gas
phase simulations
Computer
simulations of the gas-phase and gas-surface chemistries in a diamond
depositing CVD environment have previously been used to identify and analyse
functional species and reactions. This
section describes gas-phase computer simulation studies carried out by Y.A.
Mankelevich and N.V. Suetin of Moscow State University, Russia. The 3-D model devised and used was tailored
to the Bristol Hot filament CVD reactor used in the REMPI studies, and was used
to assist in the unravelling of the complex gas-phase chemistry. Previous studies of the diamond depositing
HF-CVD gas-phase environment have implemented 1-D and 2-D models, however these
have yielded poor correlation with experimental results. 3-D modelling of the gas-phase environment
was expected to describe the species and heat transfer more accurately.
The model
consists of three sections that describe the activation of the gas mixture
(i.e. gas heating, filament activation), the gas-phase processes (heat and mass
transport and reaction kinetics) and the gas-surface growth process at the
substrate. Gas-phase chemistry and
thermochemical input is provided by the GRI-Mech 3.0 reaction mechanism[17],
which details gas-phase reaction mechanisms for C / H / O reaction
mixtures. For the present application
the reaction scheme was modified by removing all oxygen containing species and
reactions. Spatial distributions of the
gas temperature, the mass and heat flux, and species concentrations, are
calculated by integrating the conservation equations for mass, momentum, energy
and species concentrations in Cartesian co-ordinates, with appropriate initial
and boundary conditions, thermal and caloric equations of state, until a steady
state regime is achieved.
The Cartesian
co-ordinates used by the model are set to mimic that of the Bristol reactor
with the (0,0,0) point defining the centre of the filament. The z-axis
is set parallel to the gas flow direction and perpendicular to the filament,
the x- and y- axes lying respectively orthogonal to the filament and gas flow,
and parallel to the filament. The model
allows a degree of flexibility in the setting of certain parameters. In the studies detailed here the less well
known parameters Q, (the rate of
atomic hydrogen production at the filament surface) and DT, (the temperature difference between the filament surface
and the gas in the immediate vicinity of the filament) were varied. The temperature drop may also be expressed
in terms of the near-filament temperature, Tnf,
where DT = Tfil
- Tnf.
3.5 3-D calculations of CH4/H2
and C2H2/H2 chemistry
Calculations
of the methyl radical number density, as a function of distance from a
filament, were compared to the previously described spatially resolved CH3
REMPI measurements taken with dilute CH4 or C2H2
in H2 gas mixtures.
Figure 3.10
shows CH3 radical concentrations predicted by a full 3-D model
calculation, as a function of distance z
from the filament, for different Tnf
and Q.
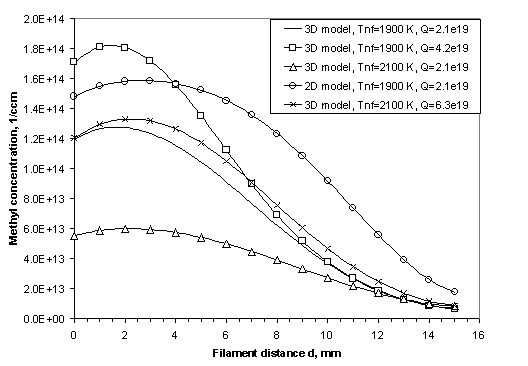
Figure
3.10 Calculated CH3 radical
concentration profiles in the model illustrating the effects of Q, Tnf
and the discrepancies introduced by a lower dimension calculation.
This diagram is included here simply to highlight the
errors that may be introduced by using a lower dimension calculation and to
show the general CH3 radial concentration trend observed with
changes in Q and Tnf.
Figure 3.11 compares the experimental CH3
radical relative number density measurements, obtained using both 1% CH4
in H2 and 0.5% C2H2 in H2 gas
mixtures, with the best fit 3-D model calculations which assume Q = 0.6 ´ 1019 cm-2 s-1
and Tnf = 2000 K (DT = 475 K).
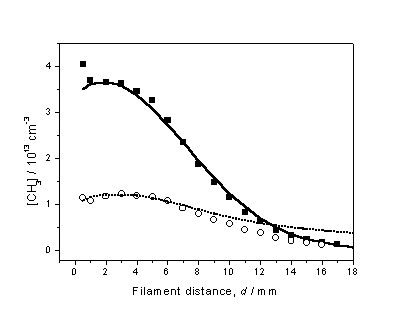
Figure
3.11 Experimentally determined d dependent [CH3] profiles
obtained using 1% CH4 in H2 (¢) and 0.5% C2H2 in
H2 (™) gas mixtures, with Tfil = 2475 K.
To establish a common vertical scale for this plot, measurements were
made while switching between CH4 and C2H2,
while maintaining a constant Tfil. The 3-D model calculations are represented
by the solid and dashed curves and, implicitly, yield the absolute number
densities shown on the left-hand axis.
With both the Q
and Tnf parameters
established, further investigations into the C2H2/H2
gas-phase chemistry could occur.
Inspection of the GRI-Mech 3.0
C / H reaction scheme reveals large variations in the
chemistry. This is due to dependence on
the local gas temperature and therefore the region studied in the reaction
chamber. Table 3.2 outlines a number of
reactions involving the production and loss of C2H2
together with calculated reaction rates for a given gas temperature.
Reaction
Rate / cm-3 s-1
Reaction 730
K 1200 K 1750 K 2000 K
H + C2H2+
M ® C2H3
+ M 1.85E
+16 4.00E +15 4.07E +14 1.64E +14
C2H3 + M ® H + C2H2
+ M 3.72E
+12 1.23E +15 1.93E +16 3.23E +16
H + C2H3 ® H2 +
C2H2 1.05E
+16 3.34E +15 5.24E +15 6.07E +15
H2 + C2H2 ® H + C2H3 7.15E +1 2.54E +9 8.58E
+12 6.97E +13
Total: C2H2
®
C2H3 8.00E
+15 -5.73E +14 -2.41E +16 -3.82E +16
H + C2H4
® H2 + C2H3 7.73E +13 7.99E +15 5.78E +16 9.71E
+16
C2H3 + H2 ® H + C2H4 7.64E +15 7.86E +15 3.35E
+16 5.47E +16
H + C2H3 + M ® C2H4 + M 3.12E +14 2.21E
+13 8.58E +12 5.93E +12
C2H4
+ M ®
H + C2H3 + M 0 5.25E +6 1.15E +12 2.38E +13
Total: C2H3 ® C2H4 7.87E
+15 -1.10E +14 -2.42E +16 -4.25E +16
C2H4
+ M ®
H2 + C2H2 + M 4.14E
+1 8.76E +10 5.94E +14 4.40E +15
H + C2H4 + M ® C2H5 + M 5.02E +15 6.14E
+14 3.55E +13 1.20E +13
C2H5 + M ® H + C2H4 + M 3.15E +11 2.29E
+14 1.47E +15 1.52E +15
H + C2H5 ® H2 + C2H4 4.32E +13 4.01E +13 3.13E +13 2.37E
+13
H2 + C2H4 ® H + C2H5 0 2.50E
+7 5.88E +10 4.25E +11
Total: C2H4 ® C2H5 4.97E
+15 3.45E +14 -1.47E +15 -1.53E +15
CH3 + CH3
+ M ®
C2H6 + M 4.22E
+14 2.77E +14 3.30E +13 1.13E +13
C2H6 + M ® CH3 + CH3 + M 6.74E +2 5.09E
+11 8.01E +14 3.02E +15
CH3 + CH3 ® H + C2H3 3.73E +11 3.25E +13 1.47E
+14 1.80E +14
H + C2H5 ® CH3 + CH3 5.39E +15 4.82E +15 3.13E
+15 2.18E +15
Total: C2H6/C2H6
® CH3 4.97E +15 4.51E +15 3.75E +15 5.00E
+15
H + C2H6
® H2 + C2H5 5.94E +14 4.55E +15 4.76E +15 3.86E
+15
C2H5
+ H2 ®
H + C2H6 7.34E
+12 8.57E +13 3.24E +14 3.97E +14
H + C2H5 + M ® C2H6 + M 1.63E +14 1.70E
+13 1.50E +12 4.98E +11
C2H6 + M ® H + C2H5 + M 0 2.10E
+8 1.71E +12 1.10E +13
Total: C2H6 ® C2H5 4.23E
+14 4.45E +15 4.44E +15 3.48E +15
Table 3.2 Gas-phase scheme including the major
elementary steps in the C2 ® C1 conversion mechanism, together with their
respective reaction rates calculated for gas temperatures observed in a hot
filament reactor. Third bodies are
represented by M; due to its large number density this is typically H2. The net reaction rates for each set of
conversions are shown in bold type.
The calculated H atom number densities at the gas
temperatures shown in the reaction scheme are 1.6 ´ 1014
cm-3 (730 K), 4.1 ´ 1014 cm-3
(1200 K), 5.7 ´ 1014 cm-3 (1750 K) and 6.2 ´ 1014
cm-3 (2000 K) respectively.
However, as we saw earlier (Fig. 3.1b), throughout the reaction chamber
the atomic hydrogen number density is greater than that calculated purely on
the basis of gas-phase thermodynamics, for any given local gas
temperature. This means that the
cooler regions of the chamber away from the filament will have relatively high
[H] with a low local gas temperature.
As table 3.2 shows, atomic hydrogen drives the C2 ® C1
conversion via a multi-step series of reactions at low gas temperatures (e.g.
730 K) whereas, at much higher gas temperatures closer to the filament, the
reverse process dominates[18]. This process is summarised in figure 3.12,
where the calculated d dependence of
the various source terms for key species, together with Tgas is shown for a 0.5% C2H2 in H2
gas mixture.
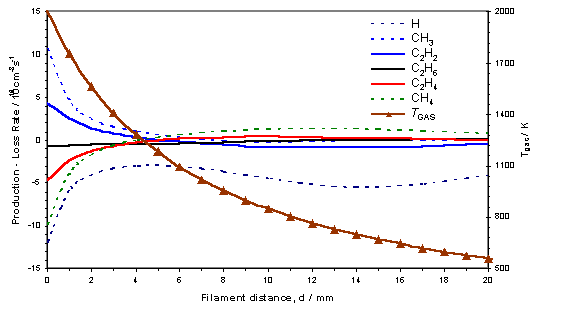
Figure
3.12 3-D model calculation showing the
source terms (production – loss terms in the gas-phase reaction scheme) for the
key species in a hot filament reactor operating with a 0.5% C2H2
in H2 gas mixture with Tfil
= 2475 K. The local gas temperature is
also shown with its corresponding scale on the right axis.
From this figure the C2 ® C1
conversion appears to maximise at d ~ 12
mm, at local gas temperatures in the range 600 – 900 K. The process of C2 ® C1
conversion proceeds by means of the multi-step addition of hydrogen to C2H2,
for example, via the scheme C2H2 ® C2H3
® C2H4
® C2H5
® CH3
® CHx
(for x = 0 – 4), which occurs preferentially in cooler regions of the
reactor. The calculations show that
approximately half of the reacted C2H2 is converted into
CH3, with the remainder being reduced to C2H4. The three-body recombination,
H
+ CH3 +
M ®
CH4 + M Reaction
3.9
is sufficiently fast at low gas temperatures to allow the
formation of CH4, which may
be recycled via diffusion to form CH3 close to the filament through
the abstraction reaction 3.5. This
effect is also shown by C2H4, which is primarily formed
in cooler regions, and may be reconverted into C2H2 close
to the filament through a series of hydrogen abstraction reactions. The produced C2H2 can
then itself diffuse to cooler regions to form C2H4 and CH4.
Close to the filament surface the unimolecular decay of C2H6
makes a significant contribution to the C2 ® C1
conversion through the reaction,
C2H6 +
M ®
CH3 + CH3 + M Reaction 3.10
In the hotter regions of the chamber, close to the
filament, interconversion between various hydrocarbon species occurs readily,
due to the high local gas temperature and atomic hydrogen number density. However, this volume is relatively small in
comparison to cooler regions in the reactor.
The rapid conversion of species at the filament is therefore
counter-balanced by the reverse reactions in the slower but more voluminous
cooler regions. The reaction time for C2
® C1
conversion is of the order 10-2 – 10-1 s and therefore
occurs slower than the fast hydrogen shift series of reactions that operate on
C1Hx and C2Hx.
The concentration distributions of key species calculated
in the 3-D model reactor are shown in figure 3.13 as a function of the z-axis for 1% CH4 in H2
and 0.5% C2H2 in H2 gas mixtures.
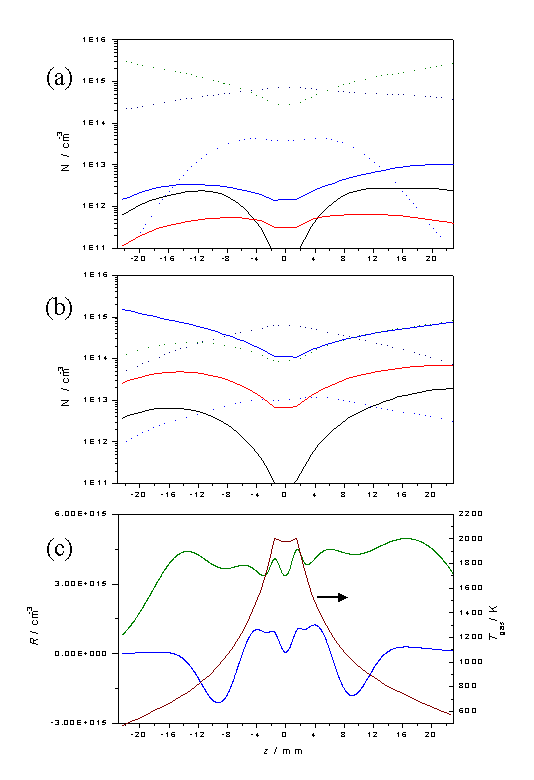
Figure
3.13 Plots showing [H], [CH3],
[CH4], [C2H2], [C2H4]
and [C2H6] as a function of z for input gas mixtures of a) 1% CH4 in H2
and b) 0.5% C2H2 in H2 using the same legend
as in figure 3.12. Calculations were
carried out assuming a chamber pressure of 20 Torr, Tnf = 2000 K and
Q = 6.0 ´ 1018
cm-2 s-1. Plot c)
shows the net C2 ® C1
conversion rate, R, for 1% CH4
in H2 (blue) and 0.5% C2H2 in H2
(green) gas mixtures, as a function of z
given the temperature profile shown.
The effect of increasing the filament temperature, and thus
Tnf and Q, can be seen by comparing plots equivalent
to those in figure 3.13, but with
Tnf = 2300 K and Q = 1.2 ´ 1020 cm-2 s-1,
these are shown in figure 3.14.
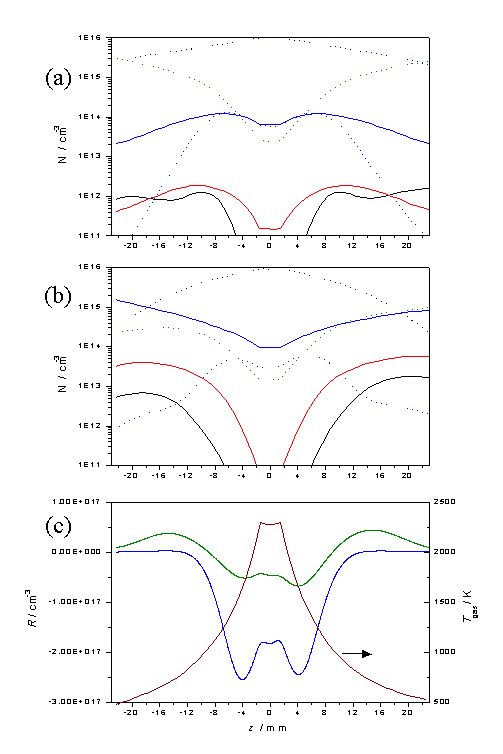
Figure
3.14 Equivalent plots to those in
figure 3.13, but with an increased filament temperature.
These figures serve to reinforce the view that the species
number densities close to the filament, and in the region z = 6 - 10 mm, where
diamond deposition would normally occur, are relatively insensitive to the
source hydrocarbon.
3.6
Conclusions
This chapter has discussed the results of a 2+1 REMPI study
of CH3 radicals in a hot filament CVD reactor operating on CH4
in H2 and C2H2 in H2 feedstock
gases. The results of these studies
were compared to 3-D model calculations to assist in unravelling the gas-phase
chemistry, in particular the C2 ® C1 conversion. Findings suggest that C2 ® C1
conversion occurs readily via a purely gas-phase route in the cooler regions of
the reaction chamber and contradicts previous assumptions that heterogeneous
processes (e.g. at the reactor walls) were necessary in order to cause the
conversion.
References
