Chapter 4 : Experimental and Theoretical studies of a nitrogen

containing HF-CVD gas-phase environment

 

 

The addition of small quantities of nitrogen to typical hydrocarbon/H₂ gas mixtures used during diamond CVD, in both hot filament and microwave reactors, has been shown to lead to enhanced deposition rates[1]^,[2], nitrogen addition appears to affect the growth habit and lead to some modest nitrogen incorporation in substitutional lattice sites[3].

 

Previous investigations at Bristol by May et al.[4] focused on diamond CVD in a hot filament reactor using CH₄/NH₃/H₂, CH₃NH₂/H₂ and HCN/H₂ gas mixtures.  The aims of these studies were to see whether use of alternative nitrogen containing precursors provided a route to enhanced nitrogen incorporation in the grown diamond film, Further aims were to unravel aspects of the chemistry prevailing in H/C/N containing gas mixtures using in-situ molecular beam mass spectrometry (MBMS), to sample the gas-phase composition in the vicinity of the hot filament.

 

The study observed diamond deposition from CH₄/NH₃/H₂ feedstock gas mixtures, provided the input gas ratio [CH₄]:[NH₃] ³ 1 was observed.  The addition of NH₃ was found to reduce deposition rates relative to those found for a simple CH₄/H₂ gas mixture.  CH₃NH₂/H₂ and HCN/H₂ gas mixtures were also shown to yield CVD diamond, with low efficiencies comparable to that found using 1:1 mixtures of CH₄ and NH₃ in H₂.  Such findings are explicable given the MBMS measurements, which showed substantial conversion of the input carbon to HCN (the thermodynamically favoured product), at the relevant process temperatures[5].  Thus it was proposed that, in the vicinity of the hot filament, HCN acts as a sink for carbon that might otherwise have participated in diamond growth.  The findings detailed in this chapter therefore build on the conclusions drawn by May et al.

 

This chapter describes a combination of experimental and 3-D computer modelling in order to provide a more detailed interpretation of the effects of controlled additions of nitrogen (in the form of N₂ and NH₃) to CH₄/H₂ process gas mixtures, in an HF-CVD reactor.  The experimental component involves use of REMPI spectroscopy to provide spatially resolved in-situ measurements of H atom and CH₃ radical number densities, and served to inspire subsequent Cavity Ring Down Spectroscopy (CRDS) measurements of NH radical column densities with the same gas mixtures, in the same HF-CVD reactor, by J.B. Wills, as a function of process conditions (e.g. feed-stock gas mixing ratio and the temperature, T_fil, of the Ta filament).  These REMPI measurements are a natural extension of our investigations of diamond CVD when using CH₄/H₂ and C₂H₂/H₂ gas mixtures in the same HF-CVD reactor detailed in chapter 3.  The results obtained are then compared with the output of a 3-D computer model, specifically tailored to this HF-CVD reactor.

 

The 3-D computer model has been described in detail in chapter 3, and therefore only changes to the previous modelling procedure will be discussed here.  The gas phase chemistry and thermochemical input is provided by the GRI-Mech 3.0 detailed reaction mechanism for C/H/N/O gas mixtures (plus one additional reaction allowing destruction of the species H₂CN), but with all reaction steps and species involving O atoms removed (shown in Appendix 6).   Comparisons between experimental and theory highlight the very different reactivities of N₂ and NH₃, in the present HF activated CH₄/H₂ gas mixtures.  These comparisons also help unravel details of the gas-phase chemistry prevailing when using H₂/CH₄/NH₃ process gas mixtures, and reveal clear evidence for a reduced H atom production rate, Q, (described in chapter 3) on the surface of the HF, when NH₃ is added to the process gas mixture.

 

The results of the CRDS study of NH[6] are also shown in this chapter purely to emphasize the accuracy of the 3-D model.

 

 

4.1      Experimental Set-up

 

Details of the HFCVD reactor, and the REMPI detection schemes used for spatially resolved measurements of H atom and CH₃ radical number densities, have been presented in chapter 2 and are essentially unchanged, save for accommodating the introduction of N₂ and NH₃ into the reaction chamber.  The H₂, CH₄, NH₃ and/or N₂ feedstock gases are metered through separate mass flow controllers, pre-mixed in a manifold, and enter the reactor through a port located above the cradle assembly, so as to maintain an overall flow rate of 100 sccm and total pressure of 20 Torr.

 

 

4.2      Modifications of the hot filament upon addition of nitrogen containing gases

 

Addition of NH₃ to a CH₄/H₂ gas mixture activated by a Ta hot filament was observed to cause a reduction in the T_fil value returned by the two-colour optical pyrometer.  No such trend was observed upon addition of a corresponding flow rate of N₂.  Fig. 4.1 illustrates these effects, via plots of T_fil versus time after the introduction of various partial pressures of NH₃ (and N₂) to an established 1% CH₄ in H₂ gas mixture.

 

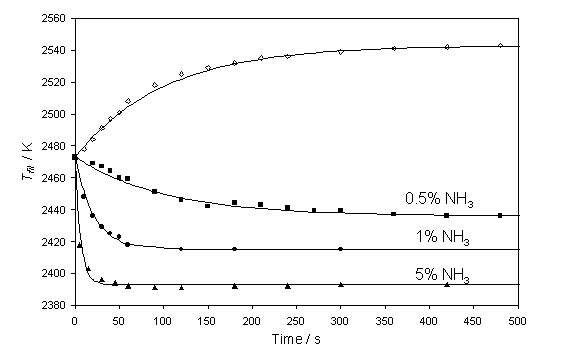
Figure 4.1  Variation in pyrometer measured T_fil as a function of time after introducing 0.5% NH₃ (¢), 1% NH₃ (˜) and 5% NH₃ (▲) to a 1% CH₄ in H₂ gas mixture.  The solid lines are best fits to these datasets in terms of equation 4.3 with t = 100 s (0.5% NH₃), 21 s (1% NH₃) and 6 s (5% NH₃).  Also shown is the time-dependent recovery of T_fil on the retardation of a 2% NH₃ flow (¯) together with a best fit with a time constant of t = 100 s.

 

In each case, the filament had been run for > 6 hrs with a CH₄/H₂ gas mixture prior to the NH₃ (or N₂) addition, and the power supplied to the filament was held constant throughout.  Clearly, both the rate and the extent of the temperature drop, DT_fil (defined as the difference between T_fil measured prior to any NH₃ addition, at t = 0 s, and the asymptotic value found at t = ¥) increase with increasing NH₃ fraction, whereas addition of 1% N₂ has minimal effect on the observed T_fil.  Each of the T_fil versus t trends measured for the various NH₃ partial pressures can be described by a function of the form:

 

                                    T_fil(t) - T_fil(t = ¥) = DT_fil exp(-t/t)                             Equation 4.1

 

with a time constant, t, that decreases as the NH₃ fraction in the input gas feed is increased.  Fig. 4.1 also illustrates how this temperature recovers with an apparently invariable time constant when the NH₃ flow is shut-off (¯).   Prior to any NH₃ addition, we foresee the filament as being largely 'carburised', i.e. to be mostly tantalum carbide with a surface that is partially covered by a coating of graphitic carbon.  Given knowledge of the input power supplied to the HF (P_input = 87 W (~12.4 V, 7.0 A) for T_fil(t = 0) = 2473 K in figure 4.1) and estimates of the power expended on H₂ dissociation (2 W) and conductive losses (10.7 W) from the 3-D modelling, we can estimate the power radiated by the HF (~74 W).  This, in turn, allows estimation of the mean emissivity, e, of the hot filament via Planck's radiation law,

 

                                                            P_rad  = e s S T_fil⁴,                                            Equation 4.2

 

where s is the Stefan-Boltzmann constant and S is the calculated surface area of the filament (0.63 cm²).  The emissivities derived, e ~ 0.56 and ~0.61, for the addition of respectively 0% and 1% NH₃ fall midway between literature values for the emissivity of TaC (e ~ 0.3)[7] and graphite (e ~ 0.9)[8] at T ~ 2500 K.  This implies that, under these conditions, approximately half the filament surface has a graphitic coating.

 

The observed time dependence of T_fil upon addition of NH₃ may be expressed in terms of dynamic competition between the adsorption, desorption and/or etching of the hot filament surface by nitrogen and carbon containing entities.  In this scheme, two limiting mechanisms merit consideration.  The first assumes that, both N and C containing species are present, and that the former are adsorbed preferentially onto the filament surface.  'N-termination' on the filament is presumed to alter the energy balance and increase the mean emissivity, leading to the observed reductions in T_fil and in Q (detailed in section 4.4).  Assuming this is so, the observed time dependence of T_fil (shown in equation 4.1) can then be rationalised by considering a simplified adsorption-desorption / etching kinetic scheme, in which accommodation of a N containing gas phase species on an available surface site, S*, leads to N-termination, i.e. via the dynamic equilibrium,

 

                                                            N + S* ¾ SN.                                                 Equation 4.3

 

The time dependence of, q, the N-terminated surface coverage, will then follow,

                                   

                                    q  = (1 - exp[-(k₅[N] + k_-5)t]                  Equation 4.4

 

where [N] is the number density of nitrogen containing species near the filament surface, and k₅ and k_-5 are, respectively, the forward and reverse reaction rate coefficients for the generic gas-surface reaction described in equation 4.3.  Fitting the experimental data for addition of 1% and 5% NH₃ to a 1% CH₄ in H₂ gas mixture with

T_fil = 2473 K (at t = 0), shown in figure 4.1, yields values of k_-5 ~ 0.01 s^-1 and

k₅[N] = 0.38 s^-1 and 0.157 s^-1, respectively.  The observed recovery of T_fil when the NH₃ flow is discontinued may also be calculated using equation 4.4.

 

It is also worth mentioning that similar decreases in T_fil have been reported previously in the case of carburised Ta filaments operating at high temperatures (T_fil > 2800 K) and constant P_input when the hydrocarbon content in CH₄/H₂ gas mixtures is suddenly reduced[9].  This may seem counterintuitive at first, since a reduction in the number density of gas-phase carbon would be expected to induce a concomitant reduction in the extent of any graphitic overcoat on the filament surface, which should therefore lead to a reduced emissivity and thus cause T_fil to rise.  This observation has been explained by realising that the graphitic ‘overcoat’ is considerably less efficient than a 'clean' TaC surface at catalysing H₂ dissociation; the observed drop in T_fil is thus attributed to the increase in the fraction of P_input expended on surface catalysed H₂ dissociation.

 

As shown previously, one effect of NH₃ addition is to convert CH₄ molecules into HCN in hotter regions of the gas.  HCN is a stable molecule in this environment, and thus acts as a 'sink' for gas-phase carbon near the filament surface.  Therefore, a second possible model for the time dependence of T_fil upon NH₃ addition presumes that, NH₃ addition has the effect of reducing the number density of gas-phase carbon available for formation of any graphitic layer on the filament surface.  This would have a similar effect to simply reducing the CH₄ input flow rate.  This, in turn, might then be expected to cause an increase in S*, capable of catalysing H₂ dissociation and could thus also give rise to the observed time dependent variations in T_fil.  Given our earlier estimates of the fraction of P_input used in dissociating H₂ molecules on the filament surface, at the comparatively low T_fil values used in this work, such an explanation seems incapable of accounting for T_fil reductions of the magnitudes observed upon NH₃ addition.

 

 

4.3      Gas-phase H atom and CH₃ radical relative number densities observed with the addition of NH₃ and N₂

 

Relative number densities of H atoms and CH₃ radicals were measured by 2+1 REMPI (in an identical manner to that used in chapter 3), as a function both of added NH₃ (or N₂) and T_fil.  Figures 4.2 and 4.3 show experimentally measured [H] and [CH₃] values, as a function of added N₂ and NH₃, for a 1% CH₄ in H₂ mixture (flow rate = 100 sccm, total pressure = 20 Torr and T_fil = 2573 K), measured at a filament distance d = 4 mm. 

 

Clearly, given the above change in filament characteristics, it was necessary to increase the power supplied to the HF progressively as the NH₃ input mole fraction increased in order to maintain a constant T_fil.

 

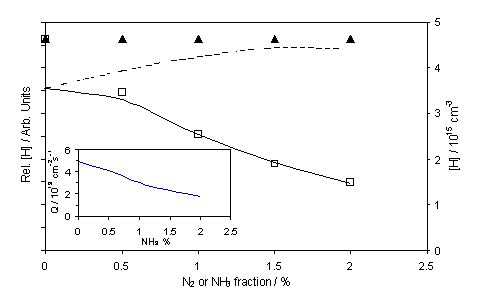
Figure 4.2  REMPI measured H atom relative number density, as a function of added NH₃ (£) and N₂ (p) to a 1% CH₄ in H₂ gas mixture.  The chamber was maintained at 20 Torr and the filament at T_fil = 2573 K.  The dashed curve shows the calculated variation in absolute [H] (right hand scale), assuming fixed values of

Q (4.92 ´ 10¹⁹ cm^-2s^-1) for T_nf = 2075 K using the previously established T_gas dependency on d.  The solid curve however shows a fit to the experimentally determined NH₃ data assuming that Q declines with added NH₃ with a function shown in the figure inset.  The theoretical and experimentally determined data were vertically scaled so as to match for 1% NH₃ addition.

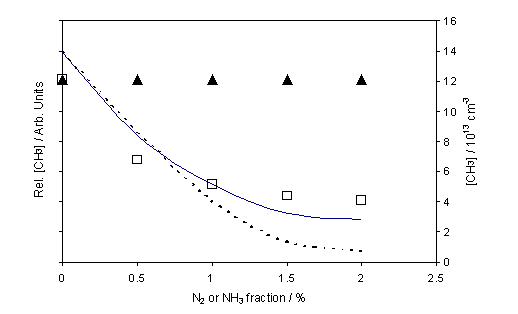
Figure 4.3  Equivalent plot showing REMPI measured CH₃ relative number density as a function of added NH₃ (£) and N₂ (p) to a 1% CH₄ in H₂ gas mixture.  The reactor conditions are identical to that stated for figure 4.2 with measurement also carried out at d = 4 mm.  The dashed and solid curves represent the calculated variation in absolute CH₃ number density given a fixed Q, and when assuming that Q varies as a function of added NH₃ as shown in the inset of figure 4.2.

 

Interpreting these, and subsequent, experimental data builds on previous modelling of the gas phase chemistry occurring in activated CH₄/H₂ and C₂H₂/H₂ gas mixtures in this same HF-CVD reactor (Chapter 3).  The modelled reactor (with no substrate present) is represented in Cartesian co-ordinates with the z-axis parallel to the direction of feedstock gas flow (input ® output) and perpendicular to the filament, the centre axis, of which, is along y.  x is orthogonal to both the filament axis and the direction of gas flow, the point (0, 0, 0) defines the centre of the filament, and d = 0 corresponds to the point (0, 0, 1.5 mm).  The model calculation extends to the volume enclosed within

x = ± 16 mm, y = ± 18 mm and z = ± 26 mm, with the gas temperature set to T_gas = 600 K at all boundaries of the numerical grid.  The positions (20 mm, 0, 0) and (0, 20 mm, 0) represent the reactor walls while (0, 0, -25 mm) and (0, 0, +25 mm) represent the gas outlet and inlet positions. 

 

The dashed lines in figures 4.2 and 4.3 show absolute H atom and CH₃ radical number densities predicted by 3-D simulations, assuming, the experimental values for T_fil  and the gas pressure, a net H atom production rate at the filament

(Q = 4.92 ´ 10¹⁹ cm^-2 s^-1), a near filament gas temperature (T_nf = 2075 K) and a d dependence for T_gas consistent with our previous measurements.  In both figures, the measured [H] and [CH₃] values appear insensitive to the addition of N₂.  This result can be readily understood by inspecting the calculated temperature (and thus position) dependent interconversion rates and number densities for the various participating species.  In the case of a 1%CH₄/1% N₂/H₂ gas mixture, N₂ is deduced to play the role of an essentially inert spectator, with a predicted fractional dissociation [N]/[N₂] < 10^-7 even at T_gas ~ 2000 K (i.e. as attained in the immediate vicinity of the HF).  Further simulations, in which this ratio was arbitrarily increased (such as could conceivably apply in the event of catalysed N₂ dissociation on the filament surface or, in the case of microwave activation, as a result of non-thermal plasma chemistry), indicate that the [N]/[N₂] ratio would have to be at least 100 times higher in order to cause a measurable reduction in [H] or [CH₃].

 

However, the addition of NH₃ into the hot filament activated 1% CH₄ in H₂ gas mixture, clearly changes the gas-phase chemistry.  The calculated z dependent interconversion rates and number densities for all major species present in a hot filament activated

1% CH₄ / 1% NH_­3 / H₂ gas mixture, displayed in figure 4.4, show this nitrogen containing precursor to be intimately involved in the high temperature gas-phase chemistry.  Temperature and pressure dependent rate constants, k(T,P), for the numerous elementary steps underpinning the H/C/N gas phase chemistry are taken from the GRI-Mech 3.0 reaction mechanism.  The addition of the highly exothermic reaction,

 

                                                H + H₂CN ® H₂ + HCN,                                           Equation 4.5

 

which was originally excluded from the GRI-Mech database due to its overall minor role in combustion analysis, curtailed the calculated build-up of unstable H₂CN in the cooler regions of the reaction chamber.

 

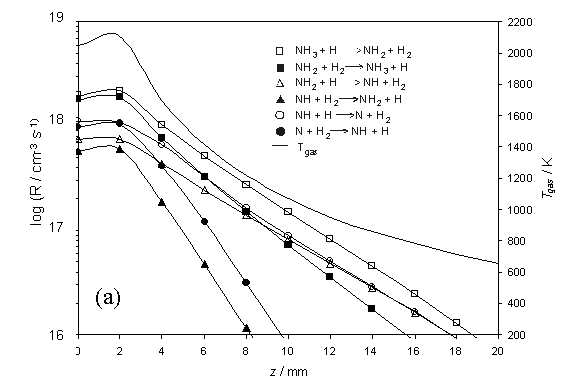
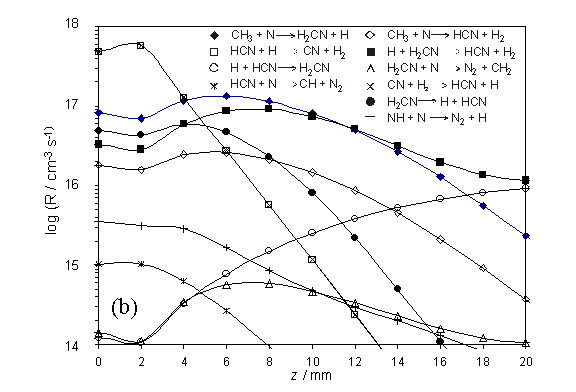
Figure 4.4  Plots showing the semi-logarithmic calculated rates, R (left-hand scale), for (a) the series of hydrogen shift reactions, NH_x + H  NH_x-1 + H₂, and (b) other selected reactions dealing with nitrogen containing species.  Both plots are shown as a function of distance z (with x = y = 0) for a chamber operating with 1% CH₄ / 1% NH₃ / H₂ and T_fil = 2573 K.  The R values were calculated assuming Q = 2.0 ´ 10¹⁹ cm^-2 s^-1, T_nf = 2100 K and a z dependent temperature profile as shown in (a) (right-hand scale).

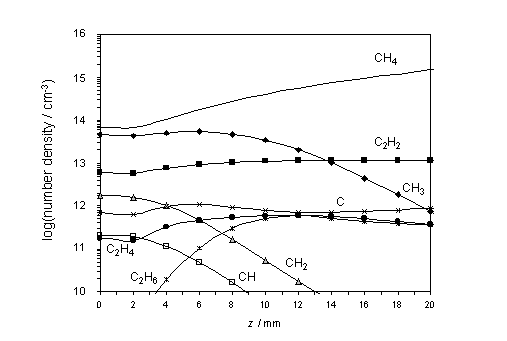
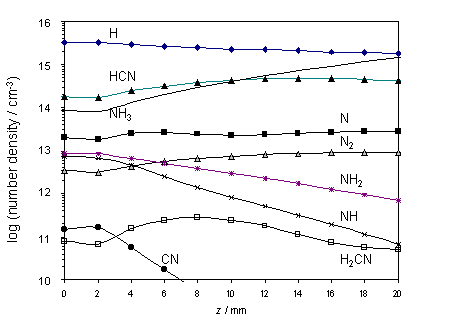
The calculated species number densities, clearly show HCN acting as a carbon ‘sink’ in both the hot and cool regions of the chamber.  This is shown in figure 4.5 together with other relevant species.

 

           

Figure 4.5  Plots showing the species number densities calculated for equivalent conditions as used to determine R in figure 4.4, for (a) species involved in the nitrogen shift reactions and (b) other important species.  Both plots are shown as a function of distance z.

 

The experimental results, shown in figures 4.2 and 4.3, and the calculated rate constants and species number densities, shown in figure 4.4, are for a constant T_fil, gas pressure and flow rate.  As the dashed lines in these figures show, no single value of Q is capable of fitting all data recorded as a function of added NH₃.  To match the experimental observations it is necessary to assume Q to be NH₃ dependent, i.e. to assume that N-termination of the HF surface causes not just an increase in emissivity but also a reduction in the mean H atom production rate, Q.

 

This much improved agreement is illustrated by the solid lines in figures 4.2 and 4.3, which demonstrates that it is possible to obtain a reasonable fit with the experimentally measured [H] and [CH₃] versus T_fil dependencies, if Q for the filament, maintained at a constant T_fil, declines with the percentage of added NH₃.  The deduced functional form of Q(NH₃; T_fil = 2600 K) is shown in the inset to figure 4.6.  Such a dependence may be considered plausible given the previous conclusions that NH₃ addition leads to modification ('N-termination') of the filament surface and of its emissivity.

 

 

4.4      Gas-phase H atom and CH₃ radical number densities in a 1%CH₄/1%NH₃/H₂ gas mixture as a function of T_fil 

 

Figure 4.6 compares H atom relative number densities measured 4 mm from the filament surface as a function of T_fil for a 1%CH₄/H₂ input gas mixture, with and without 1% added NH₃, while figure 4.7 shows the corresponding plots for the measured CH₃ radical relative number densities.

 

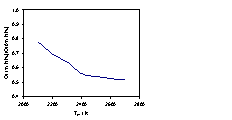
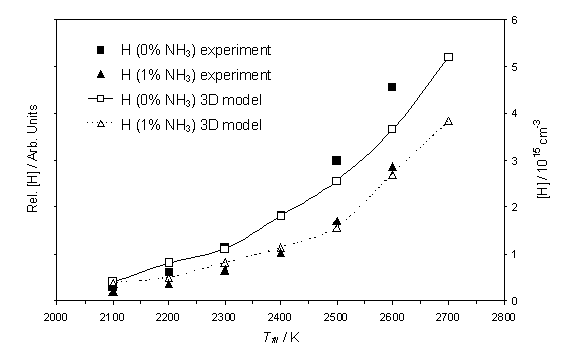
Figure 4.6  Calculated [H] and measured relative H atom number density as a function of T_fil.  Both the calculation and the measurements were carried out using a 1% CH₄ / H₂ gas mixture, with and without the addition of 1% NH₃, at 20 Torr.  REMPI measurements were carried out at d = 4 mm.

 

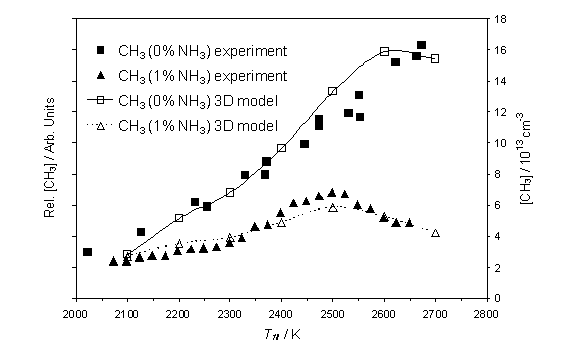
Figure 4.7  Calculated [CH₃] and measured relative CH₃ number density as a function of T_fil.  Both the calculation and the measurements were carried out using the same conditions as described in figure 4.6.

 

As shown in previous experiments in Chapter 3 (Figure 3.6), the H atom number density increases almost exponentially as a function of increasing T_fil.  The observation that the decrease in the H atom number density, with the addition of NH₃, continues throughout the filament temperature range is also shown.  As in figure 4.2, model calculations based purely on gas-phase chemistry, together with the assumption of a constant Q, suggest that [H] should increase upon addition of NH₃.  In order to obtain convergence between experimental observation and the model calculations it is necessary to assume that the NH₃ induced modification of Q is itself a function of the filament temperature.  As figure 4.6 shows, a reasonable match between experiment and theory can be obtained if the ratio Q(1%NH₃)/Q(0%NH₃) is assumed to vary with T_fil.  Figure 4.7 shows, in accord with previous findings, that [CH₃] rises smoothly with increasing T_fil for the standard 1% CH₄/H₂ mixture, but that addition of 1% NH₃ causes a marked decrease in [CH₃], most notably at high T_fil.  Both trends are reproduced well by the 3D model calculations but, again, better agreement with the trends measured in the presence of 1%NH₃ can be obtained by assuming that Q(1%NH₃)/Q(0%NH₃) is T_fil dependent.

 

The value of Q may be seen as a function of factors attributed to T_fil and the NH₃ fraction.  Let us consider both factors in terms of H production on the filament surface.  Q may be related to T_fil via the equation,

 

Q(T_fil) ~ exp(-DH_diss/RT_fil)                                         Equation 4.8

 

where DH_diss is the enthalpy of formation of H atoms from the surface of a hot filament (~240 kJ mol^-1) and R is the gas constant.  With the addition of NH₃, H production is retarded, therefore Q being by definition, the rate of H atom production on the filament surface may be expressed in terms of T_fil and %NH₃ addition by the expression,

 

Q(T_fil, NH₃) = Q₀(NH₃).exp(-DH_diss/RT_fil)                             Equation 4.9

 

where the parameter Q(NH₃ = 0) (also written Q₀) is calculated from the results of the REMPI measurements of H atom relative number densities at a given T_fil with no NH₃ added.  The effect of the Q parameter is seen in figures 4.6 and 4.7 where the best-fit ratio Q(1% NH₃)/Q(0% NH₃) = 0.57 and Q₀ = 3.6 ´ 10²⁴ cm^-2 s^-1.  The Q₀ quoted was obtained by fitting to the local maxima in [CH₃] for a 1%NH₃/1%CH₄/H₂ gas mixture at high T_fil and the measured rise in [CH₃] for the 1%CH₄/H₂ gas mixture both observed in figure 4.7.

 

 

4.5      NH radical number densities and spatial profiles in 1% CH₄ / x% NH₃ / H₂ gas mixtures.

 

Analysis of the modelling results of the z dependent species concentrations and elementary reaction rates, detailed in figure 4.5, indicate that the number density of NH radicals in the vicinity of the hot filament (>10¹² cm^-3), should be sufficient to permit their detection by a sensitive absorption method like CRDS.  Unlike REMPI, such measurements offer a route to absolute column densities, and thus provide a further test of the absolute values of Q, and their dependence on T_fil and [NH₃], returned by the gas phase chemistry modelling.  Such measurements have been undertaken by J.B. Wills⁶.  As with the REMPI measurements, number densities were determined as a function of radial distance from the lower edge of the coiled filament, and as a function of input NH₃ mole fraction.  Figure 4.8 compares the measured and predicted filament distance, d, dependence of NH radicals in a hot filament activated 1% CH₄ / 5% NH₃ / H₂ gas mixtures with T_fil = 2473 K, monitored via the R₁(2) and R₁(3) transitions of the NH(A-X) origin band.

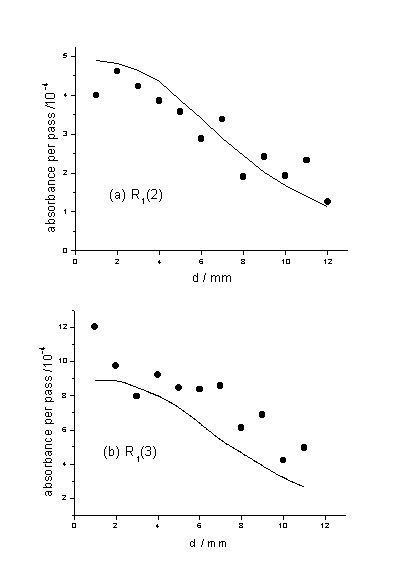
Figure 4.8  Measured (˜) and calculated(¾) d dependence of the NH absorbance.  The measured data were obtained by monitoring (a) the R₁(2) and (b) the R₁(3) transitions of the NH(A-X) origin band.

 

Naturally the NH absorbance, and thus [NH], is found to scale essentially linearly with the input NH₃ mole fraction. The level of agreement (to within ~20% in the implied absolute number densities) provides strong support for the validity of the foregoing modelling of the gas phase chemistry of H/C/N containing mixtures in a HFCVD reactor, and the spatially resolved absolute number densities returned by the simulations for all major species.  

 

 

4.6      Conclusions

 

The results presented here, and elsewhere, provide a reasonably self-consistent picture of the gas phase transformations occurring in a HF CVD reactor operating at typical modest filament temperatures when trace amounts of NH₃ are added to a hydrocarbon/H₂ gas mixture.  Input CH₄ molecules pass through a multi-step sequence of reactions en route to stable products C₂H₂ and HCN, thereby depleting the number densities of CH_x species both near the HF and in the surrounding volume, extending out to distances where the substrate would normally be positioned in a diamond growth experiment.  HCN also acts as a sink for input NH₃ molecules.  The studies detailed here show that NH₃ additions to an activated CH₄/H₂ gas mixture lead to reductions in the CH_x number density in the vicinity of the HF in two ways.  Firstly, addition of NH₃ introduces additional, purely gas-phase, CH_x loss processes.  Secondly, NH₃ additions are deduced to cause modifications of the HF surface, increasing its emissivity and thus lowering T_fil (for a given input power) and reducing its efficiency for catalysing H₂ dissociation even if T_fil is maintained constant.

 

Additional confirmation of the REMPI measurements and the modelling results was provided by CRDS analysis of NH radicals, which afforded knowledge of the radical radial number density dependence as a function of the distance from the filament.

 

It is worth noting that the modelling study predicts CN radical concentrations at typical filament – substrate distances to be < 10⁹ cm^-3.  If, as thought, nitrogen incorporation into a diamond film is carried out via CN addition into a vacant surface site, this may provide an explanation for low nitrogen doping efficiencies.

 

References