Chapter 8

Intensity Modulated Photocurrent Spectroscopy

 

8.0       Outline

 

·            This chapter presents the results of Intensity Modulated Photocurrent Spectroscopy (IMPS) experiments on boron doped diamond films.

 

·            A theory is presented to explain the results.

 

8.1       Intensity Modulated Photocurrent Spectroscopy (IMPS)

 

IMPS is electrochemical technique where the working electrode is illuminated by a sinusoidally modulated source. ¹³⁵ An AC photocurrent may be generated by the fluctuating level of illumination. The harmonic response of the photocurrent to the illumination may be phase shifted. This photocurrent may be analysed as a function of the modulation frequency of the light source.

 

It has been shown that IMPS can provide information about charge transfer ¹³⁶ and recombination ¹³⁷ at the illuminated semiconductor-electrolyte junction.

 

8.2       Experimental Set-up

 

A Solartron 1250 Frequency Response Analyser (FRA) was used to generate a sinusoidally oscillating potential. This was used to drive a light emitting diode (LED). The potential had a DC component of 4.5 V and an AC component of ±0.5 V.  The ‘turn on’ potential of the LED was approximately 3 V. At the potentials used, the intensity of the light produced by the LED was linear with respect to the applied potential. Therefore, the electrochemical cell was constantly illuminated and the light had a fluctuating component which was sinusoidal and in phase with the driving AC potential.

 

A custom built potentiostat was used which was known not to apply a phase shift to the signal. The applied DC potential between the working electrode and the reference electrode was fixed while the frequency of the light oscillation was varied. The circuitry in the potentiostat was able to accurately record signals fluctuating at frequencies up to 2000 Hz.

 

The potentiostat signal was fed into the FRA. The FRA measured the harmonic component of the signal. The quotient of this harmonic current to the harmonic component of the driving signal was then recorded as a function of the harmonic frequency. As the harmonic current was phase shifted from the harmonic light intensity, the resulting quotient was complex. A bode plot of the quotient could therefore be plotted.

 

IMPS experiments require a monochromic light source with a controllable and variable intensity.  Lasers or LEDs are commonly used to provide the light. In these studies two LEDs were used. One LED emitted light at a wavelength of 470 nm. The other LED emitted 430 nm light. The 470 nm LED was more efficient and produced a more intense light beam than the 430 nm LED.

 

The data were recorded with Z-plot software and viewed with Z-view 2 software (Scribner Associates, Inc.). The Z-view 2 software enabled curves to be fitted to IMPS curves. Values could therefore be found for the frequencies at which the maxima of the IMPS curves occurred.

Figure 8.1 shows a schematic diagram of the IMPS set-up.

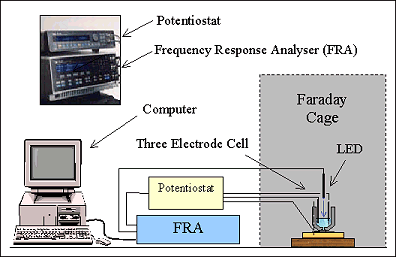
Figure 8.1

The IMPS Set-up

 

8.3       Experimental Results

 

Sample B121a was grown in a hydrogen/methane/diborane atmosphere with a [B]/[C] ratio of 254 p.p.m. in the gas phase (corresponding to a boron doping level of 4 ´ 10¹⁹ cm^-1).

 

Figures 8.2 to 8.7 show IMPS plots for B121a, which were recorded with a minimum depth of electrolyte. Details of the aqueous solutions and wavelength of the illuminating LED used are listed in table 8.1. The frequency of the AC component of the illumination was varied from 1 Hz to 4000 Hz.

 

 

 

Table 8.1

Summary of IMPS experimental conditions

 

Solution A was an aqueous solution of

0.5 mol dm^-3 H₂SO₄, 1 ´ 10^-3 mol dm^-1 FeSO₄ and 5 ´ 10^-4 mol dm^-1 Fe₂(SO₄)₃.

 

Solution B was an aqueous solution of

0.5 mol dm^-3 H₂SO₄ and 1 ´ 10^-3 mol dm^-1 FeSO₄.

 

Solution C was an aqueous solution of

0.5 mol dm^-3 H₂SO₄ and 5 ´ 10^-4 mol dm^-1 Fe₂(SO₄)₃.

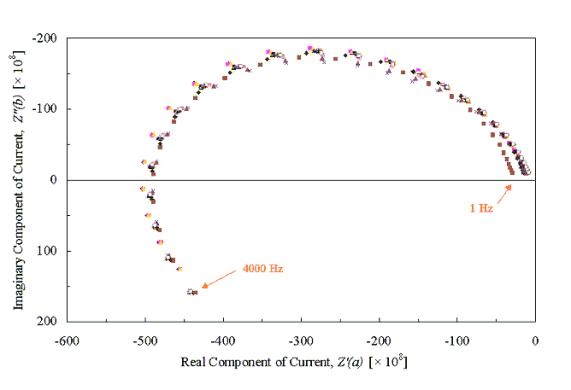
Figure 8.2 – Diamond Sample B121a, I.M.P.S. @ 470 nm, 1 mM Fe²⁺, 1 mM Fe³⁺, 1 M H⁺ various applied DC potentials, frequency range 1 Hz – 4000 Hz

 

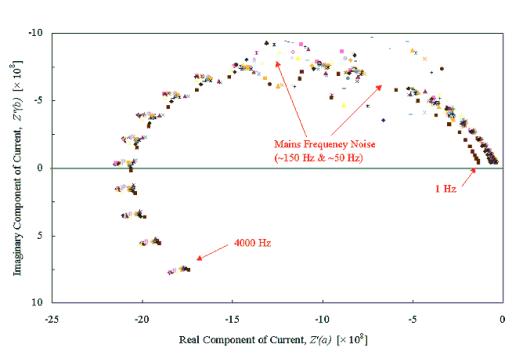
Figure 8.3 – Diamond Sample B121a, I.M.P.S. @ 430 nm, 1 mM Fe²⁺, 1 mM Fe³⁺, 1 M H⁺ various applied DC potentials, frequency range 1 Hz – 4000 Hz

 

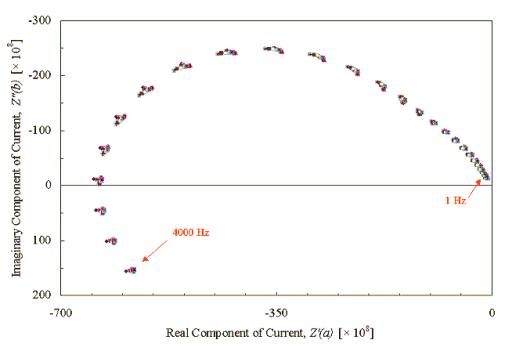
Figure 8.4 – Diamond Sample B121a, I.M.P.S. @ 470 nm, 1 mM Fe²⁺, 1 M H⁺

various applied DC potentials, frequency range 1 Hz – 4000 Hz

 

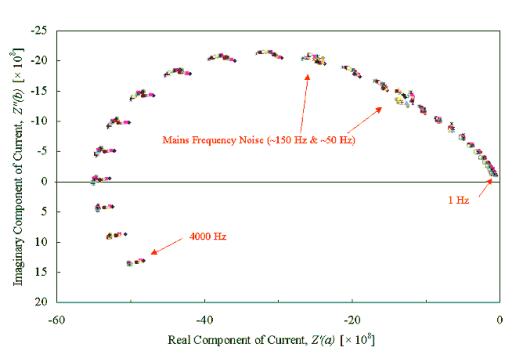
Figure 8.5 – Diamond Sample B121a, I.M.P.S. @ 430 nm, 1 mM Fe²⁺, 1 M H⁺

various applied DC potentials, frequency range 1 Hz – 4000 Hz

 

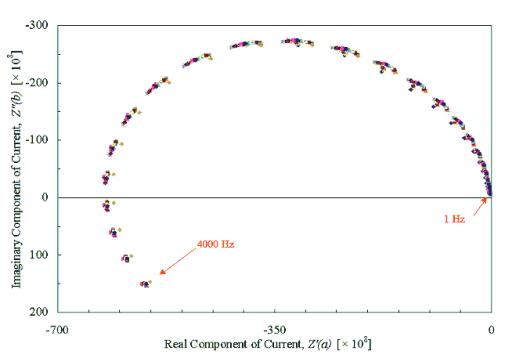
Figure 8.6 – Diamond Sample B121a, I.M.P.S. @ 470 nm, 1 mM Fe³⁺, 1 M H⁺ various applied DC potentials, frequency range 1 Hz – 4000 Hz

 

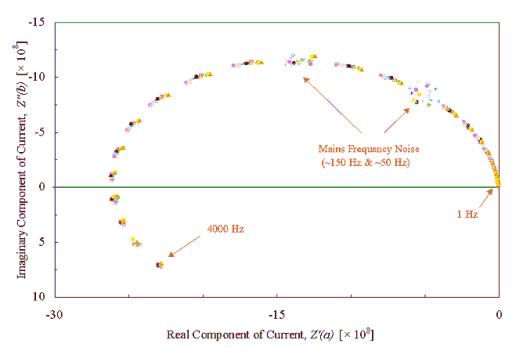
Figure 8.7 – Diamond Sample B121a, I.M.P.S. @ 430 nm, 1 mM Fe³⁺, 1 M H⁺

various applied DC potentials, frequency range 1 Hz – 4000 Hz

 

Table 8.2 – Key to DC voltages in Figure 8.2  Fe²⁺/Fe³⁺ 470 nm

 

Table 8.3 – Key to DC voltages in Figure 8.3 Fe²⁺/Fe³⁺ 430 nm

 

Table 8.4 – Key to DC voltages in Figure 8.4  Fe^{2 +} 470 nm

 

Table 8.5 – Key to DC voltages in Figure 8.5 e^{2 +} 430 nm

 

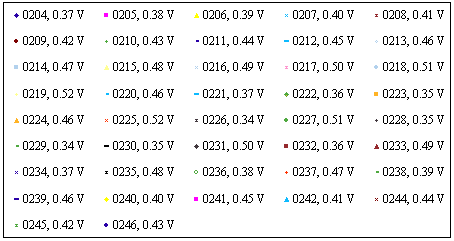
Table 8.6 – Key to DC voltages in Figure 8.6  Fe³⁺ 470 nm

 

Table 8.7 – Key to DC voltages in Figure 8.7  Fe³⁺ 430 nm

 

It can be seen that the w_max was found to be independent of the applied DC potential.

 

Table 8.8 below summarises the results for the above experiments. The value of w_max was averaged for the scans recorded with applied DC potentials between 0.40 V and 0.52 V vs. Ag|AgCl (3 M Cl^-) inclusive.

 

 

 

Table 8.8  frequencies of IMPS maxima for several experimental conditions

 

Figures 8.8 and 8.9 show graphs comparing the results for the IMPS experiments taken with an applied DC voltage of 0.46 V vs. Ag|AgCl (3 M Cl^-).  This corresponded to the open circuit potential as determined by the mAutolab and Solartron potentiostats.

 

The high frequency sections of the plots that cross the origin can be disregarded as artefacts of the potentiostat circuitry, which was considered to be unreliable above a frequency of approximately 2 kHz

 

The scans showed IMPS signals that tended to zero at high and low frequencies. These results are unusual and can be explained by the surface state model that has been developed for boron doped diamond electrodes.

 

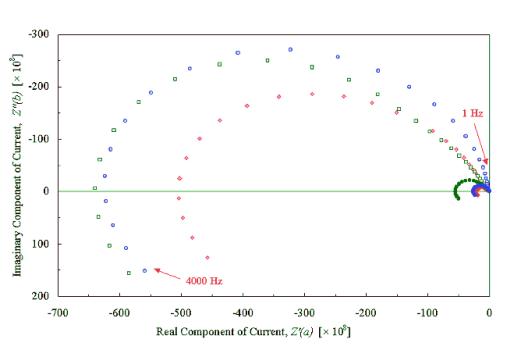
Figure 8.8 – Diamond Sample B121a, I.M.P.S. @ 470 nm & 430 nm

applied DC potentials = 0.46 V (near OCP), frequency range 1 Hz – 4000 Hz

 

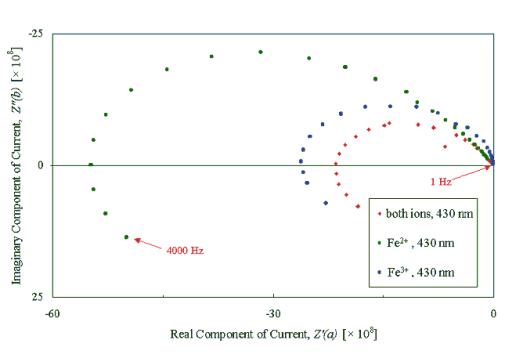
Figure 8.9 – Diamond Sample B121a, I.M.P.S. @ 430 nm applied DC potentials = 0.46 V (near OCP), frequency range 1 Hz – 4000 Hz

 

 

The IMPS results were independent of the applied DC potential.

 

The values of w_max were not effected by the excitation wavelength. The magnitude of the signals were smaller for the 430 nm experiments due to the reduced intensity of the illumination.

 

The two excitation wavelengths used were 430 nm and 470 nm. These corresponded to energies of 2.88 eV and 2.64 eV respectively. Therefore, a photocurrent was being produced by illumination with sub-bandgap radiation. This suggested that a photoexcited surface state was involved.

 

The magnitude of the responses for the different aqueous solutions are not indicative as the coloured solutions absorbed some of the light as it passed through the cell. Therefore, the transmission through different solutions varied and no compensation was made for this effect.

 

8.4              Theory

 

8.4.1    Effect of Constant Illumination on the Current Density

 

If it is assumed that illumination may cause direct excitation of valence band electrons to a surface state, then a photocurrent may be generated.  Figure 8.10 shows the effect of illumination on a system that is forward biased relative to the flat band potential.

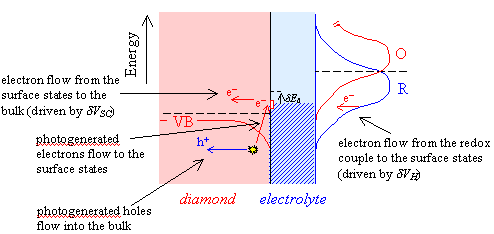
Figure 8.10  photogenerated electrons at the diamond-electrolyte interface

 

Photogenerated electrons flow to surface states while the photogenerated holes flow into the bulk. Flow of electrons from the redox couple to the surface state will be driven by the potential drop across the Helmholtz layer, dV_H. Flow of electrons from surface states into the bulk will be driven by the potential drop across the space charge region, dV_SC.

 

Considering the system in the dark as a reference and assuming no significant recombination of photogenerated electrons and holes, a series of equations can be derived for the system.

 

The general equation for the current density across Helmholtz current, j_H, (equation 4.8) is:

                                                                        (equation 8.1)

 

The semiconductor / surface state junction treated as a Schottky-diode
 (adapted from equation 4.18):

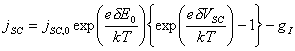                                      (equation 8.2)

 

where g_I is the current across the space charge region due to illumination.

 

g_I corresponds to the product of the charge on an electron and the number of photons absorbed per second per unit area. g_I may also been considered to be the rate of generation of surface state charge caused by illumination.

 

Kirchoff’s first law still applies and the consideration of equivalent circuits in section 6.3 can be easily adapted to include the term g_I. The effect of illumination alters the j_sc term but the other terms are unaffected.

 

Equation 7.8:

                                                                        (equation 8.3)

where dV is the applied potential relative to open circuit in the dark

 

Equation 7.9:

                                                                              (equation 8.4)

 

This leads to a version of equation 7.16 for the case where g = 1. This gives an expression relating the DC current under illumination to the potential.

 

j_I is the total current density when the system is illuminated (i.e. the sum of the current density in the dark and the photcurrent density).

 

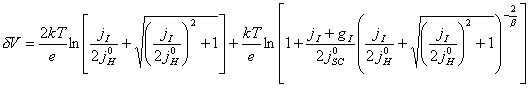
                                                                                                               (equation 8.5)

 

Figure 8.11 shows a Mathcad plot of equation 7.16 (dark) and equation 8.5 (illuminated). A value for g_I of 1 ´ 10^-2 A cm^-2 was used. This is high value and it should be noted that high levels of illumination are required to generate a significant change in the j-V curve. It can also be seen that there is a shift in the open circuit potential when the system is illuminated.

 

A series of experiments were performed where diamond samples were exposed to bright broad-spectrum (white) light.  Conclusive results were not obtained intense illumination heated the electrolyte solution and this would also have altered the measured current.

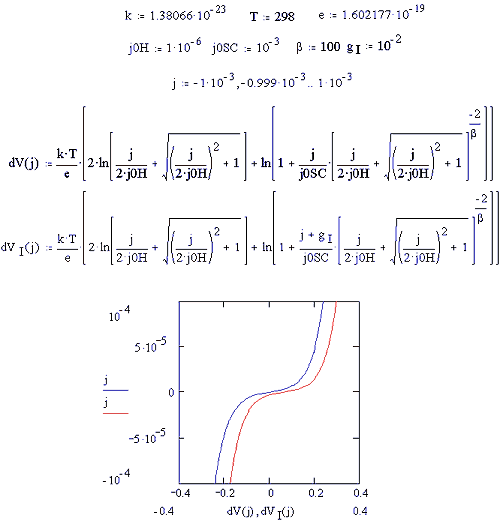
Figure 8.11  Mathcad plots of equations 7.16 (dark) and 8.5 (illuminated)

 

8.4.2    Effect of Modulated Illumination on the Current Density

 

Adapting the AC impedance model developed in section 6.4 to incorporate the current density due to a modulated intensity of illumination ().

 

Equation 7.22 states that:

                                                                                          (equation 8.6)

 

When the system is under potentiostatic control:

 

                                                                                                     (equation 8.7)

 

The current across the Helmholtz layer is given by equation 7.26:

 

                                                     (equation 8.8)

 

Adapting equation 7.28 for a photocurrent density gave:

 

                                          (equation 8.9)

where j_I is the DC current flowing while the system is under illumination.

 

Equation 7.29 can be adapted to incorporate  and :

 

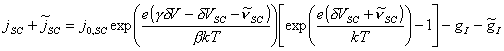
                                                                                                             (equation 8.10)

 

The term j_0,SC is defined as the open circuit potential in the dark and dV is the applied potential relative to j_0,SC.

 

As the modulations are small, equation 8.10 can be expanded using Taylor’s theorem.

 

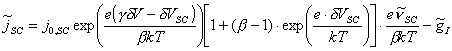
                                                                                                             (equation 8.11)

 

Equation 8.11 may be rewritten to give:

 

                                                                                (equation 8.12)

 

where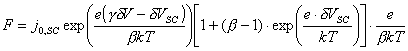     

                                                                                                             (equation 8.13)

 

Applying Kirchoff’s first law to the equivalent circuit gives equations 7.37 and 7.38.

 

                                                                               (equation 8.14)

 

                                                                            (equation 8.15)

 

The above equations may be combined to give an equation for the IMPS signal:

 

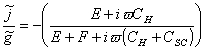                                                          (equation 8.16)

 

Equation 8.16 is a single semicircle which goes to zero at high and low frequencies. This in line with the experimental results presented in section 8.3.

 

Figure 8.12 shows a Mathcad plot of equation 8.16.

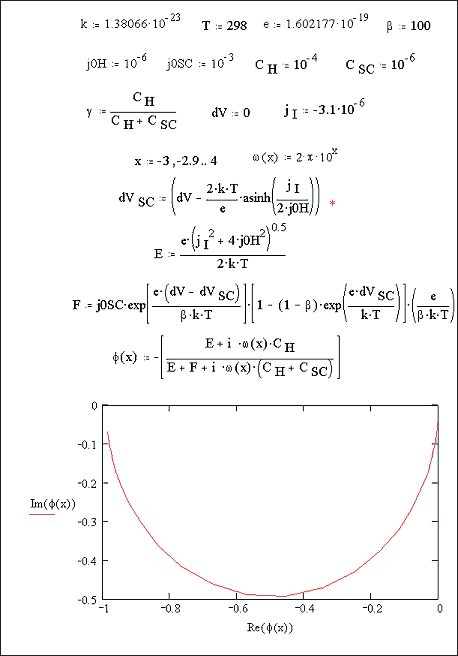
Figure 8.12  -  Mathcad plot of IMPS equation 8.16

 

8.5       Summary

 

IMPS results have been obtained for boron doped ploycrystalline diamond electrodes. Values for w_max have been obtained for the Fe^2+/3+ redox couple. The values of w_max are independent of DC potential and the choice of excitation wavelength (470 nm or 430 nm).

 

The surface state model developed for the AC impedance of the diamond electrodes has been extended to cover intensity modulated photocurrents.

 

The results suggest that charge transfer occurs via a surface state.