Chapter 5 - Plasma Temperature Measurement

“Auspicium melioris aevi”

5.1 Introduction

The rates of gas phase reactions generally depend strongly on the temperature of the gas. Recalling the diagram of Butler et al (Fig. 1.8) [[1]], CVD reactors contain an activation source (i.e. high temperature region), and cooler regions nearer the walls. Thus, the gas temperature varies spatially throughout the reactor, and hence the gas phase composition will depend on the local gas temperature (thermal chemistry), and transport properties of the gas. It is known that the transport mechanism of the gaseous species is governed by diffusion in low pressure (~20 Torr) MW and HF CVD systems. An additional complication encountered for plasma systems are reactions arising from charged species (electron- and ion-neutral chemistry). These reactions are harder to consider, as they depend critically on the electron energy distribution function (eedf) and plasma density, which are generally not known, and may vary from point to point in the reactor.

Hot filament CVD reactor gas phase temperature profiles have been actively studied, and it has been noted that large temperature gradients exist within a few mean free paths of the filament surface [[2]]. The filament is usually heated to a temperature of ~2600 K, and the substrate maintained at ~1100 K, ~5 mm from the filament. The typical gas phase temperature in the region between filament and substrate is ~1500 K, as noted in Section 1.9.5.

5.2 The source of Plasma Heating

In HFCVD, thermal energy is transferred from the hot filament to the gas during collisions between gas molecules and the filament. In MWCVD, electrons are the essential intermediate for the conversion of microwave energy to thermal motion of gas molecules. Because electrons are less massive than neutral or ionic species, they respond more readily to the oscillations of the microwave field, and thus extract significant energy from it. The microwave driving frequency, n_MW = 2.45 GHz, is therefore the maximum frequency at which electrons can oscillate in the plasma in response to the applied electromagnetic field. Electrons attempt to oscillate at this frequency, however they will also undergo collisions with gas molecules. This is the principal mechanism for transferring microwave energy to thermal energy of the gas. The microwave driving frequency, n_MW, corresponds to an angular frequency w_pe (the electron plasma frequency) given by:

Eq. 5.1

This frequency is related to the electron number density, n_e, by the following equation [[3]]:

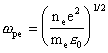Eq. 5.2

where e₀ is the permittivity of free space, and e and m_e are the electronic charge and mass respectively.

Since the microwave frequency is a (fixed) maximum, an upper limit to the electron density, n_e(max), can be found by solving for n_e in Eq. 5.2:

= 7´10¹⁰ cm^-3. Eq. 5.3

Therefore, electrons are constrained to be present in the plasma at a number density n_e<7´10¹⁰ cm^-3 (for 2.45 GHz excitation). This should be compared to the neutral gas number density of 2´10¹⁷ cm^-3, calculated assuming ideal gas law behaviour (using a neutral gas temperature of 1400 K, and 20 Torr pressure). This gives a maximum ionisation degree for the plasma (ratio of charged species number density to neutral species density) of 4´10^-7. Therefore, the plasma considered here is very weakly ionised.

The ‘cut-off density’ derived above has a physical meaning. If the cut-off density were exceeded, all the microwave energy would be absorbed by electrons in the outer ‘skin’ of the plasma - no energy would reach the centre. The electrons inside the plasma would no longer gain the kinetic energy from the microwave field, vital to create ionisation, which is in turn necessary to support the plasma state. Hence, the requirement that the cut-off density is not exceeded is related to the spatial and temporal stability of the plasma region.

The average kinetic energy of the electrons in the plasma is greater than that of the ‘heavy’ molecules and ions, as they respond more readily to the applied microwave field. Thus the temperatures of the electrons and neutral species (T_e and T_g respectively) are not the same, and two temperature fields are needed to totally characterise the plasma environment. Computer modelling of the neutral species spatial temperature profile, T_g, in the plasma has been undertaken in the work of Rau et al [[4]-[5][6]], and Grotjohn et al [[7]]. These models indicate that the plasma temperature in the discharge centre is sensitive to the gas pressure and microwave power used. Low power systems (<2 kW) appear to have T_g~2000 K, whilst temperatures ~5000 K are attained at high powers (6 kW plus) and pressures (>200 Torr).

As with studies of microwave plasma composition, measurements of the gas temperature found in the plasma are scarce. Weimer et al used a shielded thermocouple to measure a maximum T_g of 1100 K in a 170 W microwave plasma at 20 Torr [[8]]. Erickson et al measured a gas temperature of (1200±100) K using H₂ emission spectroscopy [[9]]. Gicquel et al used coherent anti-Stokes Raman spectroscopy to obtain the rotational and vibrational temperatures of H₂ [[10]]. The vibrational temperature, T_vib was found to be ~200 K higher than the rotational temperature, T_rot at ~2150 K using a microwave power of 600 W to sustain the plasma. It was assumed that T_rot was identical with the neutral gas temperature, T_g. The electron temperature, T_e was determined from T_vib and T_rot and found to be between 14000 and 18000 K and insensitive to gas-phase composition and electron density. The computer models mentioned earlier [4-7] show reasonable agreement with the experimental measurements.

5.3 Gas Temperature Determination by MBMS

The fact that the sampling efficiency (gas throughput) of the MBMS sampling probe orifice is temperature dependent [[11][12]-[13]] suggests a route for determining the temperature, T_g, of the sampled gas. The mass spectrometer signal for argon in a 2% Ar/H₂ gas mixture was found to scale as T_g^-1.6 in previous work [12,13] using an almost identical MBMS system to that employed for the present study. In the previous work, an electrically powered tungsten filament was used to heat the gas, and a thermocouple used to monitor the gas temperature close to the sampling orifice [12]. In the present work, we have assumed the same T_g^-1.6 relationship to extract gas-phase temperature information from a 2% Ar/H₂ plasma. For calibration, the room temperature signal for 2% Ar/H₂, measured prior to generating the plasma, was used. Gas temperatures determined from a 2% Ar/H₂ plasma should be very similar to those encountered in typical CH₄/H₂ CVD plasmas, as both use a small amount of a second gas, diluted in H₂. The gas temperature will therefore be largely determined by the properties of the bulk H₂.

The Ar mass spectrometer signal from a 2% Ar/H₂ gas mixture (determined previously, [12]) at room temperature, T₀, can be written as:

Eq. 5.4.

where C is a constant.

For a typical temperature determination experiment a 2% Ar/H₂ gas mixture was admitted to the CVD chamber at the process pressure (usually 20 Torr). The room temperature is known, either from the substrate holder thermocouple, or wall-mounted temperature sensor. The mass spectrometer signal for argon, I_RT(Ar) was then measured at room temperature. Values of T₀ and I_RT(Ar) were put in Eq. 5.5 to determine the value of the constant C.

Eq. 5.5

At a different gas temperature, T_g, for example during plasma excitation of the gas:

Eq. 5.6.

C was determined prior to striking a plasma, and during the experiment the argon signal was monitored. The quantities C, and I(Ar), can be substituted in Eq. 5.7, which is the rearrangement of Eq. 5.6, solved for the gas temperature, T_g.

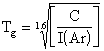Eq. 5.7

The above equation allows determination of gas temperatures from a mass spectrometric signal. The assumption made in the use of the T_g^-1.6 signal dependence relationship (Eq. 5.6) is that the dilute Ar/H₂ mixture has the same thermal properties when heated by a plasma as when heated by a hot filament. Additionally, it is assumed that the thermocouple used previously to determine the T_g^-1.6 dependence gave an accurate measure of the gas temperature. Specifically, this assumption was that the thermocouple did not act as a significant heat sink, lowering the gas temperature in its immediate vicinity.

5.4 Gas Temperature as a Function of Microwave Power - Probe 1

The dependence of the gas temperature of a 2% Ar/H₂ gas mixture on the applied microwave power was examined initially. The results are presented in Figure 5.1. Probe 1 (described in Section 3.3.1) was used for this experiment.

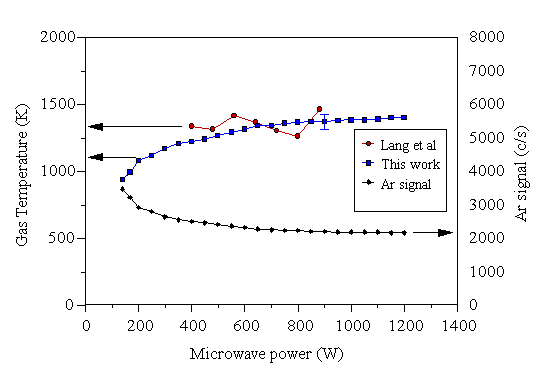
Figure 5.1 Gas temperatures determined using MBMS (probe 1), as a function of applied microwave power. The Ar signal from a 2% Ar/H₂ gas mixture is shown on the right hand axis. The gas temperature calculated using the T_g^-1.6 dependence of the Ar signal is shown on the left hand scale, with the results of Lang et al [[14]] (see text).

The temperatures measured by this technique compare well with the results of Lang et al [14], who used H₂ visible emission spectroscopy to determine the neutral gas temperature of a 1% CH₄/H₂ plasma. They reason that the Doppler temperature of H₂ can give a reliable measure of the neutral gas temperature. Their gas temperatures determined by this method for a range of microwave powers were measured at a pressure of 80 mbar (~60 Torr). Fig. 2 of reference [14] shows a linear correlation between gas temperature and reactor pressure. Extrapolation to our working pressure of 20 Torr (~27 mbar) suggests a reduction in T_g of 600 K in the data. Adopting this correction, the data of Lang et al has also been included in Fig. 5.1, and is in excellent accord with the present results. So too, is the work of Weimer et al [8] who measured a maximum gas temperature of 1100 K for a 170 W microwave plasma using a shielded thermocouple, and that of Erickson et al [9], who used H₂ emission spectroscopy to deduce a gas temperature of (1200±100) K. The agreement between the non-intrusive (optical) techniques and the present results reinforces our assumption that the presence of the sampling probe does not appreciably affect the sampled gas. The agreement with the results of Gicquel et al [10] is not so good, as a considerably higher temperature ~2150 K was measured at 600 W applied microwave power. Their measurements, however, were made approximately 25-30 mm above the substrate - well within the main bulk of the plasma. In the present experiment, at 600 W applied power the plasma encompasses 5-10 mm of the probe tip, so the current measurements were made closer to the edge of the plasma discharge, and not deep in the bulk. Given this, our measured temperatures are expected to be lower than those of Gicquel et al. Further credence will be given to this explanation in the following section where the temperature just inside, and just outside the visible plasma edge is considered.

5.5 Gas Temperature as a Function of Microwave Power - Probe 2

We have also used probe 2, which was 10 mm shorter than probe 1, to repeat the above temperature determination, and the results are shown in Fig. 5.2. Probe 2 samples a region just inside the visible plasma edge for microwave power levels >700 W. As with the gas-phase composition results using probe 2 (Section 4.9), the plasma was observed to jump to the side of the substrate holder below a microwave power level of about 600 W. The points below 600 W therefore indicate heating of the gas by the substrate heater, and microwave heating of the gas.

Figure 5.2 Gas temperatures determined using MBMS (probe 2), as a function of microwave power. Input gas composition: 2% Ar/H₂. The gas temperature was calculated from the Ar signal using Eq 5.7.

Comparison of Fig. 5.2 with Fig. 5.1 shows that the temperature of the gas sampled by probe 2 was substantially lower (~400-600 K) at all microwave powers. The gas temperature, however, rises rapidly at the highest powers as the visible plasma ball extends to encompass the probe tip, and the inside of the visible plasma region is sampled. Thus, the gas was significantly cooler at r=25 mm than r=15 mm (probe 1). This indicates that a drop of ~1000 K over a 10 mm radial distance has occurred in the vicinity of the visible plasma edge. This is evidence for a significant temperature gradient which may be responsible for the observed mass-dependent thermal diffusion effects mentioned in the previous chapters (4 and 6). Such temperature gradients are generally believed to exist between the hot discharge core, and the surrounding cool gas [[15]]. Temperature gradients of the magnitude found here are also predicted by computer models of H₂, and CH₄/H₂ microwave discharges, studied by Rau et al [4-6]. Such a temperature gradient could also explain the disagreement between the results of the previous section, and those of Gicquel et al [10]. Gicquel et al measured a gas temperature ~2150 K close to the plasma centre, whereas we determined a temperature ~1200 K approximately 5 mm inside the visible plasma edge (both at 600 W). The existence of a significant radial temperature gradient implies that the gas temperature must increase as the plasma centre is approached, qualitatively explaining the discrepancy between the results of Gicquel, and those of Section 5.4.

5.6 Vertical Plasma Temperature Profile

Using the bellows at the base of the CVD chamber it was possible to translate the substrate, and plasma, relative to the (static) sampling probe, as described in Section 4.7. This changes the cavity geometry, and hence the matching of the microwave cavity. It was found that the substrate could be translated vertically through about 40 mm, whilst maintaining a stable plasma. As noted in Section 4.7, the plasma follows the substrate holders motion to some extent (Fig. 4.29). It was therefore possible to extract a spatial (vertical) temperature profile from the plasma by using a 2% Ar/H₂ gas mixture, and the T_g^-1.6 dependence of the Ar signal. In moving the substrate holder from being almost in contact with the sampling probe (Z=6 mm), to ~Z=40 mm from the probe, the sampling point is changed from the base of the plasma, to a point approximately 10 mm from the top of the plasma (see Fig. 4.29). This is the vertical range over which it was possible to deduce a temperature profile. Such a profile is shown in Fig. 5.3, for three microwave power levels. The gas temperatures measured without a plasma present (i.e. substrate heater only, set at 973 K) are also shown.

Figure 5.3 Gas temperatures determined using MBMS (probe 1), as a function of vertical position of the substrate holder. Input gas composition: 2% Ar/H₂. The gas temperature was calculated from the Ar signal using Eq. 5.7.

The plasma temperature remains remarkably constant throughout the range studied, being slightly cooler at the lower edge of the plasma. These results compare well with those in Section 4.7 where the gaseous composition over such a vertical traverse was found to also be almost independent of the vertical sampling position in the plasma. It is also, perhaps, unexpected not to see a stronger variation of gas temperature with vertical position, in the light of the radial temperature gradient noted earlier (Section 5.5). This is perhaps because it is all too common to refer to the plasma as a ‘ball’, which implies spherical symmetry. In fact the microwave field mode is supported inside a cylindrical resonant cavity. Since this determines the electric field strength, and hence the electron density, it is physically more reasonable to expect cylindrical symmetry of plasma properties about the reactor z-axis. Cylindrical symmetry of the plasma neutral species temperature field would lead to gas temperature isotherms that were more barrel-shaped than spherical. In this case, a radial temperature gradient would be observed (as this direction is perpendicular to the isotherms at the side of the discharge), but no strong vertical dependence of the gas temperature would be seen, as this direction is parallel to the isotherms at the side of the plasma.

5.7 Effect of Substrate Temperature on Gas Phase Temperature

The effect of substrate heating on the gas temperature has been studied. To do this, room temperature calibration of a 2% Ar/H₂ gas mixture was carried out, as described for the other experiments in this chapter. A plasma was struck under standard conditions (1000 W microwave power, 2% Ar/H₂, 20 Torr pressure), with no applied substrate heating. The substrate was allowed to heat up until a constant thermocouple temperature (due solely to plasma gas heating) was reached (~650 K). The first Ar signal was recorded under these conditions, then the substrate heater set to a slightly higher value than that read by the thermocouple. The substrate heater was switched on, and the second Ar signal measurement made at a slightly higher temperature. The temperature was incremented, and Ar signal measurements made across the range of operation of the heater (up to ~1100 K). The temperature of the plasma gas was determined from the Ar signal using Eq. 5.7, and is shown in Fig. 5.4.

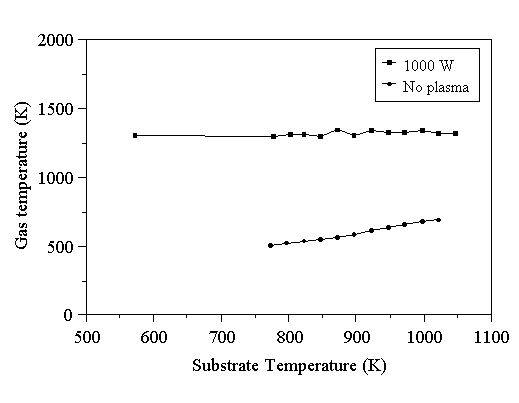
Figure 5.4. Gas temperatures determined as a function of substrate heater temperature. Conditions: 1000 W microwave power, 2% Ar/H₂ gas mixture at 20 Torr, 204 sccm total flow rate.

In the presence of a 1000 W plasma, the gas temperature is insensitive to the substrate temperature over the range examined here. This was not found to be the case when a plasma was not present in the reactor - the gas temperature was then found to increase with the substrate temperature. The most probable explanation for the observed behaviour is as follows. The temperature field in the reactor strongly affects the motion of gas molecules. The temperature field found in the presence of a plasma was different from that found when only substrate heating was applied. The plasma is a strong heat source, and therefore heat will diffuse away from the plasma. Cooler gas may diffuse into the plasma region, however by the time it has reached the sampling region it will have become heated by collisions with gas molecules in the plasma. Hence, in the presence of a plasma, the temperature field in the sampling region is determined by collisional heating. When the plasma is not present, substrate-heated gas molecules can rise into the sampling region without their temperature being raised by collisions with hot plasma gas. In fact, the effect of collisions of the substrate-heated gas with the cooler, unheated gas is to reduce the temperature of the substrate-heated gas as the vertical height above the substrate heater is increased. This was the behaviour observed in Section 5.6.

5.8 References