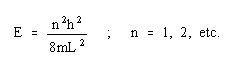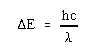Particle in a Box Theory - A Brief Summary

Absorption of electromagnetic radiation by chemical systems is due to the promotion of electrons. According to Quantum Theory, electrons in atoms (and hence molecules) can only occupy certain individual and well defined energy levels. Electrons can move between these orbitals, but can never occupy an energy value between the defined levels. Hence, it follows that a certain, precise amount of energy is needed to move the electrons between these energy levels. This energy is found in a photon of given frequency. When electrons decay to the ground state the same energy is released again (as heat or a photon or both)

Using the de Broglie relationship,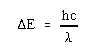where h is Planck's constant, c is the velocity of light, and lambda is the wavelength, we can verify that this energy is equivalent to the near Infra Red region for conjugated cyanine dyes.

The delocalization of the pi electrons along the conjugated carbon chain shifts the energy needed for the electronic absorption down into the IR region, and the wavelength of the transition increases with the length of the conjugated system.

This system can be treated theoretically by the "free electron" model, as proposed by Kuhn. This model states that if the absorption is due to transitions between energy levels of the pi electrons are those in the visible region, the pi electrons can then be treated as "freely" in motion along the conjugated chain. This is a "particle-in-a-box" system, one of the simplest applications of quantum mechanics. It assumes that the electrons are not hindered in their motion along the chain, but at the end of the chain there lies an energy "wall" which prevents any possibility of escape, by providing a huge energy potential.

According to quantum mechanical theory, the behavior of a particle is completely specified by its wave function, according to the Schroedinger equation.

The Cyanine Dye System

According to Kuhn's model, the "box" is the chain of conjugated double bonds with "walls" at the nitrogens. We can predict the energies of the levels available to the pi electrons. The lowest energy (longest wavelength) transition corresponds to promotion of an electron from the highest filled level (HOMO) to the lowest vacant level (LUMO).

The value of this highest filled level is determined by the Pauli Exclusion Principle, which limits the number of electrons in each level to two with opposed spins.

Estimation of the effective box length is much more difficult. The problem is to decide on the locations of the "walls". Kuhn assumed that the chain ends extend one bond distance past each nitrogen. Thus L may be taken as the sum of the bond lengths between the two nitrogens plus one additional bond distance at each end. Because of the delocalization the carbon-carbon bonds should all be equivalent with bond lengths of about 1.39 angstroms, as in the benzene molecule. For the carbon-nitrogen distance the average of 1.47 angstroms (C-N) and 1.28 angstroms(C=N) may be used, and 2 x 1.47 angstroms accounts for the extra distance at each end.

Particle in a box theory therefore explains how the presence of a conjugated chain of carbon atoms can lead a compound to absorb light in the coloured or near IR regions when the natural atomic absorbtions would be in the invisible UV area of the spectrum only.

Application of the Scrodinger equation for energy levels in a 1 dimensional box will give an estimate of the frequencies involved.