Conical Intersections

13.1 What is a conical intersection?

Figure 12.1 illustrates what we will be concerned with in this section – a conical intersection between (adiabatic) potential energy surfaces. Figure 13.1 (below) shows another view of this conical intersection.

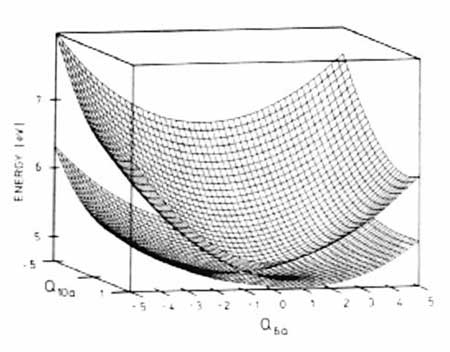Figure 13.1 - Conical intersection of the adiabatic S1 and S2 PE surfaces in the two-dimensional space spanned by the tuning mode Q6a and the coupling mode Q10a[32]

Conical intersections are interesting, firstly for the simple reason that they exist – between adiabatic surfaces, where we would often expect an avoided crossing. The distortion observed at a conical intersection is a consequence of the breakdown of the Born-Oppenheimer separation.
At a conical intersection, one can distinguish two directions, X₁ and X₂, such that if the energy in the subspace (the branching space) of these two geometric variables (combinations of the bond lengths, angles, etc.), the potential energy would have the form of a double cone in the region of the degeneracy. The remaining n–2 directions define the crossing surface (the intersection space) over which the energies of ground and excited states are equal. A movement in the plane (X₁, X₂) from a point on the intersection will result in the degeneracy being lifted. The two vectors X₁ and X₂ correspond to the gradient difference vector and non-adiabatic coupling vector, respectively. See Figure 13.2 and equations (13.1) and (13.2) (below).

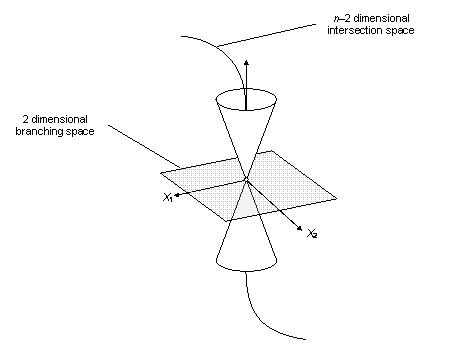Figure 13.2 - A conical intersection as described by a double cone geometry using two variables, X1 and X2

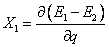(13.1)

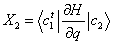(13.2)

The special case of a conical intersection is also sometimes termed a Jahn-Teller distortion, following the advent of the Jahn-Teller theorem concerning such intersections in 1937.[34]
Conical intersections differ topologically from the accidental meeting of energy surfaces – this is the essence of a Jahn-Teller distortion, where it is shown that, for a conical intersection, the wavefunction changes sign when transported (adiabatically) round a closed loop in the area of the intersection.
The conclusion can be drawn from this that somewhere inside the loop, there must be a single point where the wavefunction is degenerate – i.e. a conical intersection, leading to a transition between surfaces. Longuet-Higgins derived a topological test for locating a conical intersection based on this principle, further using it as an argument as proof that the non-crossing rule does not apply to polyatomics (the opposite of which was suggested by Naqvi (see section 11).
The remarkable feature of Longuet-Higgin’s test is that it enables one to locate the conical intersection purely from the wavefunction without any prior knowledge of its existence.
This sign reversal in the wavefunction is often termed the geometric phase (or Berry’s phase) effect. Such non-adiabatic behaviour is, of course, not fully accounted for by the Born-Oppenheimer approximation, yet it has been shown that the geometric phase (GP) effect has a quantifiable effect on the reaction probability in molecular scattering calculations at high energies, for instance.

We have seen an example of a conical intersection present in pyrazine (Figure 12.1 and Figure 13.1); conical intersections also exist in the H₃ system, the H₄ system, HNO (H + NO), H+SiO, H+F₂, ozone, NO₂, Li+H₂, and HCN, to name but a few.

13.2 Features of conical intersections

We discussed, in section 12, the probability of transitions between adiabatic surfaces at a near intersection, and the diabatic representation of such crossings.
The main feature of a conical intersection is its non-adiabatic nature – that is, that the breakdown of the Born-Oppenheimer approximation allows non-adiabatic electronic transitions to take place. Clearly, it is simple to visualise how an actual intersection facilitates easier transitions than an avoided crossing. In fact, an actual intersection (i.e. a conical intersection) allows radiationless decay (or non-absorbing when considering the transition from lower to upper surfaces). This is illustrated in figure 13.3:

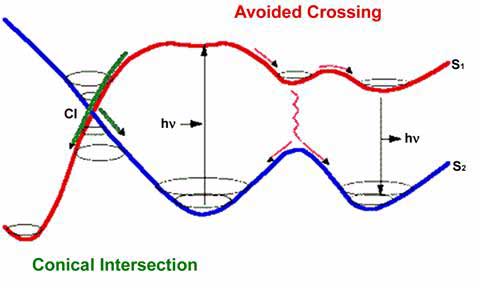Figure 13.3 - Radiationless decay at a conical intersection (M.A. Robb, “What is a Conical Intersection?”, King’s College, London)

This is an important consideration in processes such as photodissociations, isomerisations, charge-transfers, exchange collisions and energy transfers.
Worth and Cederbaum, for instance, have proposed the conical intersection is an important feature in biological systems for the mediation of ultra-fast electron transfers.[35] Jimeno, et al. discuss conical intersections in a study of H+SiO collisions, with reference to circumstellar SiO maser radiation, which can be used in the identification of long-period variable stars.[36]