a) Use the Product Rule to differentiate the function:

p(q) = (q - 4)(q - 1)

b) Multiply out the brackets in p(q). Then show that the differential of p(q) in this form is the same as that obtained in part (a) above.

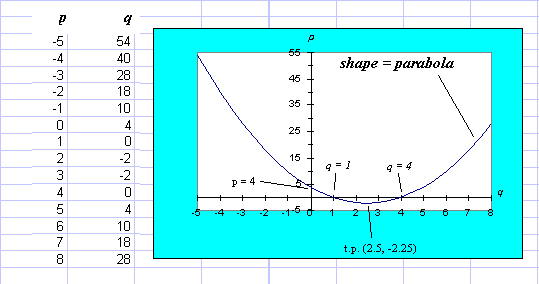
c) Determine the co-ordinates of the turning point of p(q), and prove whether it is a maximum or a minimum.

d) Sketch the curve p(q).

e) What is the area beneath this curve between q = 0 and q = 1 ?

1) Product Rule: dp/dq = u.(dv/dq) + v.(du/dq), where u = (q - 4) and v = (q - 1).

So, du/dq = 1, and dv/dq = 1

Therefore the Product Rule gives:

dp/dq = (q - 1).1 + (q- 4).1

= 2q - 5

b) Multiplying out the brackets gives: p(q) = q² - 5q +4

Differentiating this gives: 2q -5, as we found before.

c) At the turning point, dp/dq = 0, so 2q - 5 = 0, so q = 2.5. Putting this value back into p(q), we find that p = -2.25. So the turning point is at (2.5, -2.25).

d²p/dq² = +2, which is positive. This means the turning point is a minimum.

1. We know the curve crosses the p-axis at +4. We can also see from part (a), that if q = +1 or q = +4, then p(q) = 0, i.e. it crosses the q-axis at +1 and +4. Since the curve is a function of q², it will be parabola. So the curve looks like:

Need to label every point where the curve cross an axis, plus the t.p, plus label the axes correctly.

e) Area is given by: =           =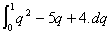

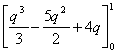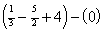
     Area = 1.833 sq. units 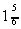    (= sq.units)