a) Use the Product Rule to differentiate the function:
p(q) = (2q - 2)(3q + 1) (8 marks)
b) Multiply out the brackets in p(q) given in part (a). Then show that the differential of p(q) in this form is the same as that obtained in part (a) above. (8 marks)
c) Determine the coordinates of the turning point of p(q), and prove whether it is a maximum or a minimum. (8 marks)
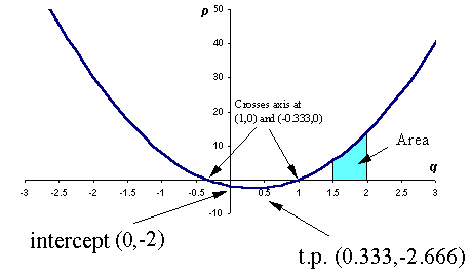
d) Sketch the curve of p(q) versus q between q = -3 and q = +3. (8 marks)
e) What is the area beneath this curve between q = 1.5 and q = 2 ? (8 marks)
a) dp/dq = (2q - 2).3 + (3q + 1).2 = 6q - 6 + 6q + 2 = 12q -4 [8 marks]
b) Multiplying out gives: p(q) = 6q2 - 4q - 2, so dp/dq = 12q - 4, as above. [8 marks]
c) At the turning point, dp/dq = 0, so, 12q - 4 = 0, meaning q = 0.333.
Substituting this value back into the original equation, we get the value of p = -2.666.
So the coords of the t.p are: (0.333, -2.666).
d2p/dq2 = +12, which is +ve, which means the t.p. is a minimum. [8 marks]
d) The curve is a function of q2, so it will be a parabola. We know it has a minimum t.p., so it will be a 'U'-shaped curve. The intercept will be at q = -2. From the original equation we can see that p = 0 when either (2q - 2) = 0 or (3q + 1) = 0, that is, when q = +1 or q = -0.333. We now have enough information to sketch the curve.

[8 marks, given for correct shape, and labelling of t.p and intercepts]
e) The trick here is to realise that we can integrate the equation in either of its forms. Since we haven't yet covered how to integrate functions of the form given in (a), we will integrate instead the expanded version we calculated in (b).Area = 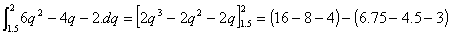
= (4)-(-0.75)
= 4.75 sq.units. [8 marks]