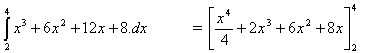
1. Answer all parts (a) to (c).
Consider the function y(x) = (x + 2)3.
(a) Differentiate this function (without multiplying out the brackets) (4 marks)
(b) Multiply out the brackets and differentiate it again, confirming that your answer agrees with that obtained in part (a) (4 marks)
(c) Determine the co-ordinates (x,y) of the stationary point(s). (8 marks)
(d) Do the stationary point(s) correspond to local maxima, minima, or point(s) of inflection? (8 Marks)
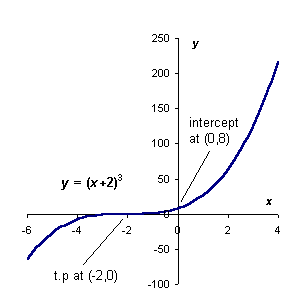
(e) Hence sketch this function between x = -4 and x = +1. (8 marks)
(f) What is the area beneath this curve between x = 2 and x = 4 ? (8 Marks)
a) Using Function Of Function Rule: dy/dx = 3(x + 2)2.(1) = 3(x + 2)2
b) Multiplying out gives y = x3 + 6x2 + 12x + 8,
so dy/dx = 3x2 + 12x +12 = 3(x + 2)2 as before.
c) At the t.p., dy/dx = 0, so 3(x + 2)2 = 0, so there's only one solution at x = -2.
Feeding x = -2 back into the original eqn, we get that the t.p is at: (-2, 0).
d) d2y/dx2 = 6(x + 2), and at x = -2 this has a value of 0. So the t.p. is a point of inflexion!
Checking the gradient either side of the t.p.: at x = -3, dy/dx = +3, so it's increasing.
At x = -1, dy/dx = +3, so it's increasing too. So the t.p. is a +ve pt of infection.
e) When x is very large and +ve, y is v. large and +ve. When x is large and -ve, y is large and -ve. When x = -2, y = 0, and this is the t.p. When x = 0, the intercept y = 8.

f) We need to integrate it in the expanded form from part (b):
Area =