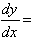1. (a) 2e^x      (b) 2x - e^x      (c) - 5e^-5x      (d) 5/x      (e) 2/x      (f) -1/x

2. (a) 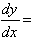e^x - 2 with the value -1 at x = 0.

(b) 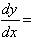2x + 2e^x with the value 18.78 at x = 2.

(c) 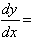e^x(x³ +3x² -2) with the value 5.437 at x = 1.

3. These are to practice the function of a function rules (Chain Rule). The important thing is the differentiation, not necessarily the simplification afterwards.

(a) 2(3x + 1).3 = 6(3x + 1)

(b) ½(2x⁴ - 5)^-½(8x³) =

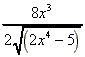
(c) x.3(2x + 3)².2 + (2x + 3)³ = 6x(2x + 3)² + (2x + 3)³

(d) x².½(x-2)^-½.1 + 2x(x-2)^½ =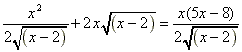

(e) { (x+2).1 - (x+1).1 } / (x+2)² = 1 / (x+2)²

(f)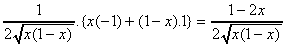

(g)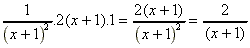

(h) 5exp (x² + 1).2x = 10x exp(x² + 1)

(i) -5(ln (3x + 1)^-2). =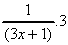

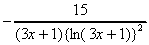
4.

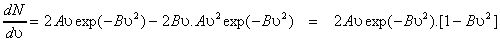
The stationary value of N(ν) is therefore given by equating the factor in the [ ] to zero which leads to:

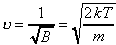
Examination of the distribution function itself shows that it is a product of a function ν² which rises with increasing ν and a function exp(-Bν²) which falls with increasing ν, both being positive functions. This stationary point must therefore be a maximum. Substitution of the given values of the parameters then leads to a most probable speed of ν = 422 m/s. You might like to draw out this function to show them what it looks like...