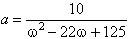
These are to be discussed in your tutorial in week 3.

1. (a) Calculate and write down the values of the function;

for values of x equal to -2, -1.5, -1, -0.5, 0, 0.5, 1, 1.5, and 2, and plot these as a graph.

Can you relate the shape of this graph to the various terms in the equation? [Hint: start with just the term 1, then include the term -2x, then finally consider what the term x³ does for large positive and for large negative values of x].

(b) Molecules absorb far-infrared radiation because it excites their rotation. The absorption coefficient (a) of a given liquid varies with the frequency (ω) of the radiation according to;

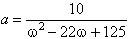
Write down the values of the function a for ω equal to 7, 9, 10, 11, 12, 13 and 15, and plot these as a graph.

For what value of the frequency is the absorption a maximum? What do you notice about the shape of this graph? [Note: with appropriate parameters this function describes the shapes of the lines in many kinds of spectroscopy].

2. Sketch the graphs of the following two functions by considering the nature of the terms in their equations:

(a) ,

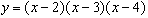[Hint: By examination you should be able to spot values of x for which y must be zero. Then consider the behaviour for large positive and large negative values of x].

(b)

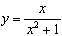
[Note: this second function is another spectroscopic lineshape function, where x is the frequency offset from line centre].

3. Use the general formula for the differential of powers of x to differentiate the following:

(a) x⁵ (b) 2x² (c) 7x³

(d) 0.5x⁴ (e) ¼x⁶ (f) 100x³⁴

(g) 14.6x³ (f) 0.05x^23.2 (h) 510³ x⁴

4. Use the general differentialion formula to calculate the following:

(a) dm/dp if m = 2p³ (b) dy/dt if y = 15t (c) df/dh if f = 5h⁴

(d) dE/dz if E = 15z⁸ (e) dβ/dx if β= 3x³ (f) dφ/dλ if φ= ¾λ⁶

(g) dΨ/dξ if Ψ= 2x¹⁸ (h) dΖ/dζ if Ζ= ½ζ³ (i) d£/d¥ if £ = 21¥³