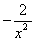 (b)
(b) 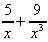 (c)
3x (d)
(c)
3x (d) 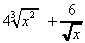
These are to be discussed in your tutorial in week 10.
1. Differentiate each of the following functions with respect to x:
(a) sin (4x) (b) cos (&pi-2x) (c) sin xcos x
(d) esin x (e) ln (cos x) (f) cot x
2. Each hydrogen atom in a hydrocarbon molecule in its lowest energy state oscillates at a frequency of 9x1013 s-1 with an amplitude of ±10pm. The expression for the time dependence of the displacement of a hydrogen atom from its equilibrium position is x = x0 sin (2t). Differentiate this with respect to time. Hence find its maximum velocity, and the maximum kinetic energy of vibration of a mole of such hydrogen atoms.
3. Integrate with respect to x
(a) 3x2 (b) 4x5 -3x2 +2 (c) 1 - 2x7
4.Integrate:
(a) 4t2 (b) 8m3 -2 (c) 4Φ4 - &Phi (d) 120ξ79 + ξ2 (e) φ3+4φ -2
5. What is the area under the curves:
(a) y = 3x2 + 1 between x = 1 and x = 4 ?
(b) p = 2q3 - 2 between q = 5 and q = 6
(c) λ = 5θ - θ2 between θ = 0 and θ> = 1
6. Integrate the following with respect to x:
(a) 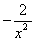 (b)
(b) 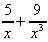 (c)
3x (d)
(c)
3x (d) 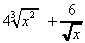
(e) e6x (f) exp (-3x) (g) 4e2x
(h) 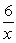
(i) 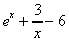 (j) 3cos x (k) 2sin x
- 3sec2 x (l) sin 5x (m) 4cos 2x
(j) 3cos x (k) 2sin x
- 3sec2 x (l) sin 5x (m) 4cos 2x
 To answers
To answers