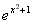 . (Note
- This exp is not the same EXP on your calculator, which refers
to 10x)
. (Note
- This exp is not the same EXP on your calculator, which refers
to 10x)
Variants of the Exponential Function
In most applications the exponent is not simply x, but
some function of x, or the exponent is multiplied by some
other function of x.
Notation: We normally write the exponential function as
y = ex, but if the exponent
is a function (e.g. x2 + 1), it's often
easier to write it as y = exp(x2
+ 1), which is equivalent to 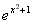 . (Note
- This exp is not the same EXP on your calculator, which refers
to 10x)
. (Note
- This exp is not the same EXP on your calculator, which refers
to 10x)
Examples
y = ebx, y = e-bx, y
= 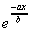 ,
,
y = e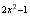 or y = exp(2x2 - 1)
or y = exp(2x2 - 1)
y = 5ex, y = 5x.e-bx,
y = (x2 - 1)e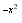 , etc.
, etc.
The reason why ex is so important is that it is the only function which doesn't change when you differentiate it.
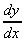 = ex
= ex
Examples
1. y = 5ex, 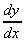 = 5ex
= 5ex
2. y = 3ex + 2, 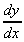 = 3ex
= 3ex
3. y = ebx, use chain rule with
u = bx, 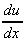 = b
= b
and y = eu, 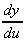 = eu
= eu
So 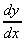 =
= 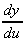 .
. 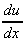 = bebx
= bebx
Alternatively, using the sequential rule:
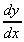 = ebx .
b
= ebx .
b
So a general result is
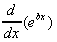 = bebx
= bebx
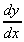 = -e-x
= -e-x
5. y = exp(x2 + 1), 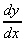 = exp(x2 + 1) . 2x
= exp(x2 + 1) . 2x
6. y = x.e-bx. This requires the product rule
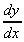 = u
= u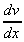 + v
+ v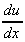 = x(-be-bx) + e-bx.(1)
= (1 - bx)e-bx
= x(-be-bx) + e-bx.(1)
= (1 - bx)e-bx
7. What is the gradient of the curve y = 5e-2x
+ 1 at the point x = 2?
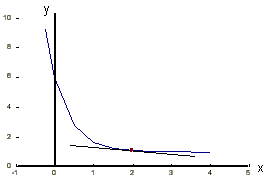
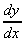 = -10e-2x,
and at x = 2, slope = -0.183.
= -10e-2x,
and at x = 2, slope = -0.183.
6. Logarithmic Functions
If we have the relationship
then there must be the inverse relationship such that
We call the function, f (y), the logarithm to base
a.
There are 2 types of logarithm in common use:
a) Common logs have base 10 and are written log10x
b) Natural logs have base e and are written logex
or ln x
So, if
y = ex, then ln y = x
y = 10x, then log10 y
= x
Laws of Logarithms
Examples
1. ln 2 + ln 3 = 1.792 = ln 6
2. ln x + ln (x2+1) = ln {x.(x2+1)}
= ln (x3+x)
3. ln 6 - ln 3 = 0.693 = ln 2
4. ln (x+1) - ln (3-x2) = ln
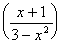
5. ln x + ln (x+3) - ln (x2+4)
= ln 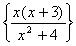
6. ln (x2 + 1)3
= 3ln (x2+ 1)
7. ln (x2+3)x+1
= (x+1) ln (x2+3)
8. ln 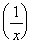 = ln(x-1)
= -ln x, (important)
= ln(x-1)
= -ln x, (important)
Numerical Example: when x =2,
9. ln 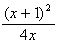 = ln
= ln 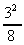 = ln
= ln 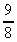 = 0.118
= 0.118
or = 2ln (x+1) - ln (4x) = 2ln 3 - ln 8 = 0.118
The Differential of ln x
It can be shown that, if
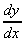 =
= 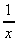
We can now use this, together with the Product, Chain and Sequential
Rules to find the Differentials of log functions.
Examples
1. y = ln (ax + b)
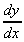 =
= 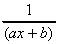 a
=
a
= 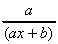
2. y = ln (2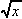 ) + 3x2 = ln (2x½)
+ 3x2
) + 3x2 = ln (2x½)
+ 3x2
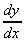 =
= 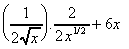 =
= 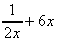
3. What are the stationary points in y = ln(x) - x?
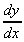 =
= 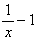
So the slope = 0 when 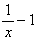 = 0, i.e.,
when x =1, and y = -1.
= 0, i.e.,
when x =1, and y = -1.
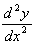 = -
= -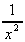 , which
at (1,-1) is -ve, so it is a maximum.
, which
at (1,-1) is -ve, so it is a maximum.
 Next lecture
Next lecture