Definite & Indefinite Integrals
There are 2 types of integral - (i) Indefinite, in which
we aren't given the limits of integration, i.e. x=a
to x=b, and (ii) Definite, in which we are
told a and b and so we can calculate a value for
an area.
Indefinite integrals
If the differential of x3 is 3x2,
then
![]() 3x2.dx = x3
3x2.dx = x3
But 3x2 is the differential of x3-1
and x3+8, etc. so that this reversal
is not unique - we've 'lost' the constant!
So in general, 3x2 is the differential
of x3+k where k is any
constant - known as the 'constant of integration'.
We write this as: ![]() 3x2.dx
= x3 + k
3x2.dx
= x3 + k
Integration 'Magic' Formula
Since integration is the reverse of differentiation, for any polynomial y(x) = xn, the integral is given by:
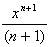 + k, (except for n = -1)
+ k, (except for n = -1)
In words: Add one to the power, then divide by the new power. Then add k.
Examples
1. ![]() x2.dx =
x2.dx = 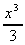 + k
+ k
2. ![]() 20x4.dx
= 4x5 + k
20x4.dx
= 4x5 + k
3. ![]() 7x.dx =
7x.dx = 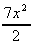 + k
+ k
4. ![]() a.dx = ax + k
a.dx = ax + k
Roots follow the same rule
5. ![]()
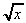 .dx =
.dx = ![]() x½.dx
=
x½.dx
= 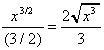 + k
+ k
Inverse powers follow the same rule
6. ![]()
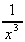 .dx =
.dx =
![]() x-3.dx =
x-3.dx = 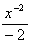 = -
= - 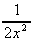 + k
+ k
This is true so long as the exponent is not -1. ![]()
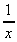 cannot be calculated using this
formula because we get a divide by zero error.
cannot be calculated using this
formula because we get a divide by zero error.
We can use other variables as well
7. ![]() 2m2.dm
=
2m2.dm
= 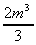 + k
+ k
8. ![]() 5
5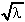 .dλ =
.dλ = 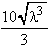 + k
+ k
9. ![]()
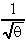 .dθ =
.dθ = ![]() -½.dθ =
-½.dθ = 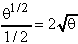 +k
+k
Sums of terms
Just as in differentiation, a function can by integrated term by term, and we only need one constant of integration.
10. ![]() 3x2 + 7x.dx
=
3x2 + 7x.dx
= ![]() 3x2 +
3x2 + ![]() 7x = x3 +
7x = x3 + 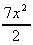 + k
+ k
11. ![]()
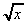 +
+ 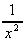 +
+ 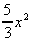 + 4x3.dx
=
+ 4x3.dx
= 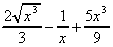 + x4 + k
+ x4 + k
Definite Integrals
We now know how to integrate simple polynomials, but if we want
to use this technique to calculate areas, we need to know
the limits of integration. If we specify the limits x
= a to x = b, we call the integral a definite integral.
To solve a definite integral, we first integrate the function
as before, then feed in the 2 values of the limits. Subtracting
one from the other gives the area.
Example
1. What is the area under the curve y(x) = 2x2 between x=1 and x=3? (Note: this is the same problem we did graphically earlier).
Area = 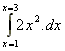 we write the limits at the top
and bottom of the integration sign
we write the limits at the top
and bottom of the integration sign
= 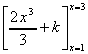 we use square brackets to
indicate we've calculated the indefinite integral
we use square brackets to
indicate we've calculated the indefinite integral
= (18 + k) - (2/3 + k) feed in the larger value, then the smaller, and subtract the two.
= 18 - 2/3
= 17.33 sq. units (compare the approximate value we got graphically of 17¾).
Note: the k's cancel. So when we evaluate a definite integral we can ignore the constant of integration.
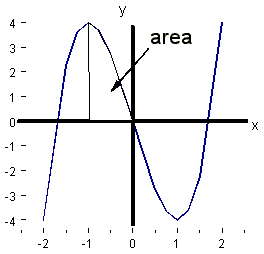
2. What is the area under the curve y(x) = 2x3
- 6x between x = -1 and x = 0?
A = 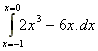
= 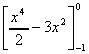
= (0) - (½ - 3) = 2½ sq.units
3. What is the enthalpy of a gas at 20 K given that its heat capacity
as a function of temperature is given by C = 2T2,
over the range T = 0 K to 30 K?
The enthalpy of a gas, H, is given by the area under the curve of heat capacity vs temperature. In most cases, we approximate it by saying that the heat capacity doesn't change much with T, so is in fact a constant. In this case the enthalpy is just given by H = C(T2-T1) since
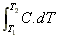 = [C.T]
= [C.T]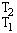 = C(T2
- T1).
= C(T2
- T1).
However in this question, we are asked for a more accurate answer, and are told C is not constant, it's a function of T.
So H = 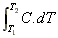
= 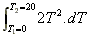 =
= 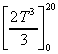 = (16000
/ 3) - 0
= (16000
/ 3) - 0
= 5333.3
= 5.3 kJ mol-1
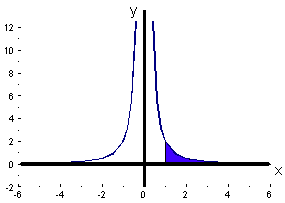
4. What is the area under the curve y(x) = 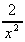 between x = 1 and x = infinity?
between x = 1 and x = infinity?
A = 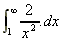
= 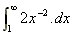
= [-2x-1]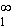 =
= 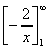
= (0) - (-2) = 2 sq.units.
Consider the function y(x) = 2x within the
limits x = -2 to +1.
A = 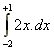 = [x2]
= [x2]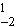 = (12) - (-22) = -3
units
= (12) - (-22) = -3
units
What does negative area mean?
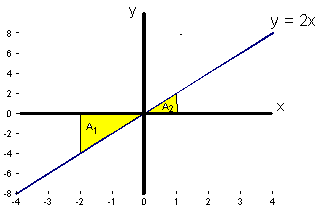
The area A1 = ½ x 4 x 2 is below the x axis and is counted as -ve.
The area A2 = ½ x 1 x 2 is above
the x axis and is counted at +ve.
Therefore it is always a good idea to sketch a curve before you integrate, to see if it goes -ve anywhere between the limits.
For any function for which the differential has been established, reversal of the process gives the integral.
Examples learn these!
1. Exponential Functions
![]() ex.dx = ex + k
ex.dx = ex + k
![]() eax.dx
=
eax.dx
= 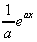 + k
+ k
2. Logarithmic Functions
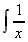 .dx = ln x + k (this is the one we cannot do using the 'magic formula').
.dx = ln x + k (this is the one we cannot do using the 'magic formula').
![]() ln x.dx = x.(ln x - 1) + k
ln x.dx = x.(ln x - 1) + k
3. Trigonometrical Functions
![]() cos x.dx = sin x + k
cos x.dx = sin x + k
![]() sin x.dx = - cos x + k
sin x.dx = - cos x + k
![]() tan x.dx = - ln (cos x) + k
tan x.dx = - ln (cos x) + k
Examples
1. What is the area under the curve y(x) = 3e-5x from x = 1 to x = infinity ?
A = 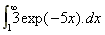
= 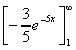
= (0) - (-0.004) = 0.004 sq.units
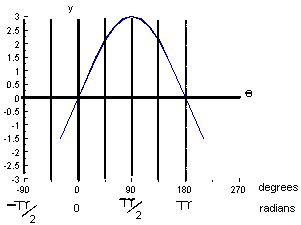
2. What is the area under the curve y(θ) = 3sin θ between θ = 0 and 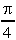 ?
?
A = 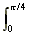 3 sin θ.dθ
3 sin θ.dθ
= [-3 cos ]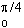
= (-3 x 0.876) - (-3)
= 0.373 sq.units
3. Integrate y(x) = 4cos x + 3e2x - 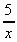
![]() 4cos x + 3exp(2x) -
4cos x + 3exp(2x) - 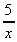 .dx
.dx
= 4sin x + 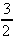 e2x- 5ln x + k
e2x- 5ln x + k