1S Summer Exam 2005 - Calculus Dr Paul May

1. Answer all parts (a) to (d). All parts carry equal marks.

Determine the following:

1. dy/dx    if    y = 9x³
2. dk/dp    if    k = 3p² + 2p - 5
3. dβ/dθ    if    β = 7tanθ
4. dj/dm    if    j = 10e^-190m

(4 marks)

2. Answer all parts (a) to (d). All parts carry equal marks.

Differentiate the following functions with respect to x, and simplify the result where possible:

1. y = (7x + 5)(10 - 5x)
   
   
2. y = 4x²¹ln x
   
   
3. 
   
   
4. y = 5sin (x⁶ - 2x⁷)
   
   

(8 marks)

3. Answer all parts (a) to (c).

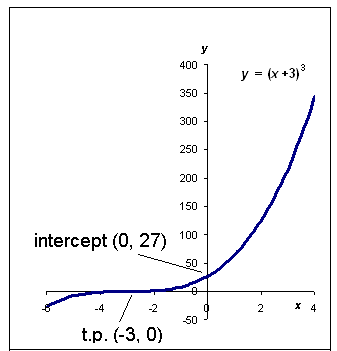
Consider the function      y(x) = (x + 3)³.

(a) Differentiate this function (without multiplying out the brackets) and thence determine the co-ordinates (x,y) of the stationary point(s).

(4 marks)

(b) Do the stationary point(s) correspond to local maxima, minima, or point(s) of inflection?

(4 Marks)

(c) Hence sketch this function between x = -5 and x = +1.

(4 Marks)

Answers

1)

1. dy/dx = 27x2
2. dk/dp = 6p + 2
3. dβ/dθ = +7/cos²θ
4. dj/dm = -1900e^-190m

2)

a) Product Rule:    (7x + 5).(-5) + (10 - 5x).7    =   45 - 70x

b) Product Rule:    4x²¹(1/x) + (ln x. 84x²⁰)   =   4x²⁰(1 + 21ln x)

c) Quotient Rule:       =   

d) Funct. of a Funct.:    5cos(x⁶ - 2x⁷)(6x⁵ - 14x⁶)   =   5(6x⁵ - 14x⁶)cos(x⁶ - 2x⁷)

3) a)

Using Func. of Func. Rule, dy/dx = 3(x + 3)².(1)   =    3(x + 3)²

At the t.p., dy/dx = 0,    so 3(x + 3)² = 0,    so there's only 1 soln at x = -3.

Feeding x = -3 back into the original eqn, we get that the t.p is at: (-3, 0).

b) d²y/dx² = 6(x + 3), and at x = -3 this has a value of 0. So the t.p. is a point of inflection!

Checking the gradient either side of the t.p.:    at x = -4, dy/dx = +3, so it's increasing.

At x = -2, dy/dx = +3, so it's increasing too.

c) When x is very large and +ve, y is v. large and +ve. When x is large and -ve, y is large and -ve. When x = -3, y = 0, and this is the t.p. When x = 0, the intercept y = 27. Students must label axes, t.p. and intercept on graph.