1S Summer exam 2007 - Calculus Dr Paul May

1. Answer all parts (a) to (d). All parts carry equal marks.

Determine the following:

(a) dy/dx if y = 270x⁶⁷

(b) du/dg if u = 1.62g³ + 5g – 3×10⁶

(c) dΩ/dΞ if Ω = 3tan Ξ

(d) d!/dö if ! = 9 exp(–7ö) + 6ö
(4 marks)

2. Answer all parts (a) to (d). All parts carry equal marks.

Differentiate the following functions with respect to x, and simplify the result where appropriate:

(a) (b) y = 9e^6x cos x

(c) (d) y = 6 ln
(8 marks)

3. Answer all parts (a) to (c).

The function has a stationary point at r = ‑ ¥

a) Differentiate this function and thence determine the co-ordinates (r,y) of the remaining stationary point.
(3 marks)

b) The second differential of this function is:

Determine whether the stationary point you just found is a local maximum or minimum.
(3 Marks)

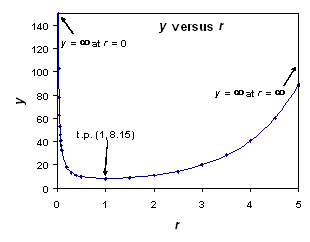
c) Hence sketch this function between r = 0 and r = 4.
(6 marks)

Answers

1)

a) dy/dx = 18090x⁶⁶ b) du/dg = 4.86g² + 5

c) dΩ/dΞ = 3 / cos²Ξ d) d!/dö = ‑63 exp(‑7ö) + 6

2)

a) Rules for Indices: y = x^‑3 – x^4/5 + 3x^‑1/2 dy/dx = ‑3x^-4 – (4/5)x^-1/5 – (3/2)x^-3/2

=

b) Product Rule: 9e^6x ( ‑sin x) + (cos x) 54e^6x = 9e^6x (6cos x ‑ sin x)

c) Quotient Rule:

d) Funct. of a Funct.: dy/dx =

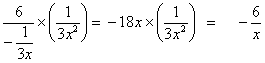
Alternatively, by the Laws of Logs,

6 ln is the same as ‑6 ln(‑3x), so dy/dx =

3) (a) Quotient Rule: dy/dr = (r.3e^r ‑ 3e^r.1) / r² = 3e^r(r ‑ 1) / r²

For turning point, 3e^r(r ‑ 1) / r² = 0, so either: r² = ¥ Þ r = ¥,

or 3e^r = 0 Þ r = ‑ ¥

or (r - 1) = 0, Þ r = 1

The last answer is the required one.

When r = 1, y = 3e¹/1 = 8.15. So the turning point is at (1, 8.15).

b) Putting in the value of r = 1, we get d²y/dr² = 3e, which is +ve, so the t.p. is a local minimum.

c) Sketch: (must get correct shape, label axes, and indicate t.p. for full 6 marks).

When r = 0, y = ¥.

When r = large, the e^r term makes y = ¥

When r = a small number (e.g. 1/100), the r in the denominator makes y very large.