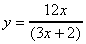1S Summer Exam 1998 - Calculus Dr Paul May

1) Determine the following:

a) dy/dx if y = 3x⁴     b) dy/dm if y = 2m⁹ + 5m⁴ - 1

c) dy/dx if y = -8 sin x     d) dp/dq if p = 510⁴ e^-q     (7 marks)

2) Differentiate the following functions with respect to x, and simplify the result where possible:

a) y = (x + 5)(x - 3)     b) y = x³ cos x

c) 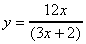     d) y = ln (4x² - 1)      (7 marks)

3) Consider the function y(x) = (x + 1)³.

a) Differentiate this function (without multiplying out the brackets) and thence determine the co-ordinates (y,x) of the stationary point(s).      (4 marks)

b) Do the stationary point(s) you have just found correspond to local maxima, minima, or point(s) of inflection?      (4 Marks)

c) Hence sketch this function between x = -3 and x = +1.      (3 marks)

Answers

a) dy/dx = 12x³         b) dy/dm = 18m⁸ + 20m³

c) dy/dx = -8 cos x         d) dp/dq = -510⁴e^-q

2) [1 mark for (a), 2 marks for the rest].

a) Product Rule: (x + 5).1 + (x - 3).1 = 2x + 2

b) Product Rule: x³(-sin x) + (cos x).3x² = 3x² cos x - x³ sin x

c) Quotient Rule: =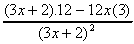

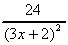
d) Function of a Function: =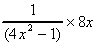

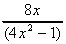
3a) This is a function of a function, so use Chain Rule or Sequential Step method:

If we let u = x + 1, then du/dx =1,

and y = u³, so that dy/du = 3u², i.e. dy/du = 3(x + 1)²

then dy/dx = dy/du du/dx = 3(x + 1)²      [2 marks]

The turning point will be when this is equal to 0, i.e. when 3(x + 1)² = 0, which occurs at only one value of x, namely x = -1. (Note that even though the function is cubic, and therefore we would normally expect 2 turning points, because it is such a symmetrical function both t.p.s overlap at the same point!).      [1 mark]

Substituting this value of x back into the function we get that the coords of the t.p. are at (-1, 0).     [1 mark]

1. To find whether the t.p. is a max or min, we first calculate the value of d²y/dx². We can do this by using the Chain Rule again.

d²y/dx² = 6(x + 1). [1 mark]

So at x = -1, d²y/dx² = 0, which means it's a point of inflection.     [1 mark]

To find out the shape of the inflection we must examine the sign of the gradient (dy/dx) either side of the t.p.

So, at, say, x = -2, dy/dx = +3, which is +ve.

And at say, x = 0, dy/dx = +3, which is also +ve.     [2 marks]

Putting in some easy-to-calculate values of x, we get:

when x = 0, y = 1

when x = -1, y = 0 (the t.p.)

when x = large and +ve, y = very large and +ve

when x = large and -ve, y = large and -ve.

And we know the gradient is +ve either side of the t.p.

So the curve looks like:

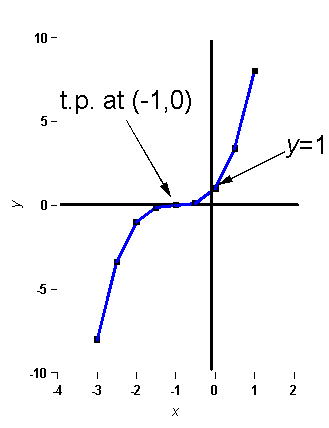
[3 marks total, given for correct shape, position of t.p., and labelling of coords of t.p. and y-intercept.]