or: introducing the sheep horn effect.
| An experimental challenge: will this molecule racemize easily? |  |
|  |
Helicenes are benzologues of phenanthrene.
With four or more rings
(tetrahelicene, or [4] for short, pentahelicene [5], etc.) the compounds exist
in two helical, enantiomeric forms, with C2 symmetry.
Racemization
experiments, carried out in the seventies, gave surprising results (see table).
Not only did racemization occur at lower temperatures than expected from
hardware models; the barriers even showed a tendency to level off for a
higher number of rings:
Very recently (more than twenty years after the measurements) three groups, remarkably close in space and time, but independently, performed calculations on the racemization process for the compounds [4] to [9], published in two papers:
A preliminary web poster (ECCC1, November
1994) showed an animation of the racemization of octahelicene (which can also be
found in Henry Rzepa's collection of hyperactive
molecules and on J.Gosper's Re_view
page).
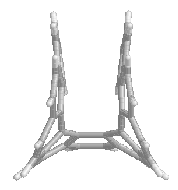 The
calculations confirmed that for [4] to [9] the racemization occurs via a
symmetric transition state (TS).
The
calculations confirmed that for [4] to [9] the racemization occurs via a
symmetric transition state (TS).
For [4] this TS is flat. In the larger
compounds this is obviously not possible and the TS adopts a kind of saddle
shape, with Cs symmetry (mirror plane).
This model explains why the energy barrier is not simply rising with an
increasing number of rings.
In the ground state, the helical forms with
C2 symmetry, the strain increases regularly with every extra ring
that is added.
In the Cs structures, this strain is more severe
and the barriers increase going from [4} to [7].
In the [7] TS however, the
end rings are almost parallel to each other. One or two extra rings added are
hardly distorted and less extra strain is introduced.
So one would expect the
barrier to decrease rather than increase for a higher number of rings, as is
actually found in the calculations for [8] and [9] (not in the
experiment, however no error is given for these measurements).
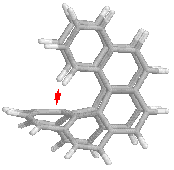 On the
other hand, larger values of n, the number of rings, introduce a new
complication. In the Cs structure, the end rings bend inside and
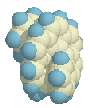
approach the central part of the molecule, as can be seen in the side view on
the right. It reminds me of the horns of certain types of sheep.
On the
other hand, larger values of n, the number of rings, introduce a new
complication. In the Cs structure, the end rings bend inside and
approach the central part of the molecule, as can be seen in the side view on
the right. It reminds me of the horns of certain types of sheep.
Calculations suggest that the Cs structure with the mirror plane is relatively stable indeed, even to such an extent that it becomes an intermediate, a local minimum, 33.7 kcal above the helical ground state. A difference which is in between that of hexa- and heptahelicene! (Also calculated with AM1, which underestimates the experimental barrier. Grimme (ref. 2) showed that DFT calculations are the most accurate for this type of structures.)
This result implies that the actual transition state, the maximum in the
racemization path, is asymmetric. The potential energy surface around the
Cs structure appears to be rather flat with respect to the dihedral
angles defined along the inner rim of the helix.
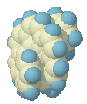
On its way from
Cs to helix the structure passes through a conformation that
resembles the [9]TS (+ an extra benzene ring) and subsequently the [8]TS (+ a
naphthalene unit attached to one end, structure on the left).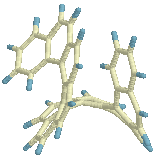
 Up to this point, the
energy is still rising! Closer inspection reveals that this is caused by the
'sheep horn' effect: the 'extra' naphthalene unit is not flat anymore, but
forced outwards so as to avoid the central bridge. So while in the pure [8]TS
the energy falls when one end of the molecule rotates underneath the other end
on its way to the helix, in the [10}TS this is compensated for by the strain in
the other end of the molecule.
Up to this point, the
energy is still rising! Closer inspection reveals that this is caused by the
'sheep horn' effect: the 'extra' naphthalene unit is not flat anymore, but
forced outwards so as to avoid the central bridge. So while in the pure [8]TS
the energy falls when one end of the molecule rotates underneath the other end
on its way to the helix, in the [10}TS this is compensated for by the strain in
the other end of the molecule.
By approximation (what an AM1 calculation is anyway) the [10] transition
state (left) is some 5.9 kcal above the symmetric Cs structure
(above, right), and the calculated racemization barrier is 39.6 kcal/mol. This
is much higher than calculated for [8] and [9].
Energy diagrams can be
found on a separate page.
So, a question for the experimentalists, what is the 'real' value?
And,
synthetic chemists, think of the nice structures you can
make if you can trap the relatively stable intermediate and connect
(photochemically?) the two end rings, lying side by side . . .
In the mean
time we'll have to continue our calculations using better, more laborious
methods.
And, now we are at it, take dodecahelicene, or, extrapolating even further, cut the coiled part of your telephone cord.....
| Switch to Java (Jmol) version (updated August 2004). | Switch to Netscape plug-in (e.g. Chemscape Chime) version. |