As an example, consider HCl:

We can think of a wavefunction in which the bond is formed between H and Cl by pairing an electron in the hydrogen in the H 1s orbital with one in the Cl 3p_z orbital.

This describes covalent bonding. Let’s call this wavefunction 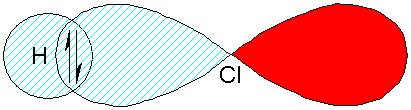Y_cov.

Y_cov

The energy of this wavefunction is e_cov.

However, this wavefunction doesn’t give the full picture of bonding in HCl: because the electrons are paired, it doesn’t allow both electrons to be simultaneously on the chlorine atom. It is only a partial description. Chlorine is highly electronegative, so it is quite likely that a full description would allow more polar structures to play a part in the full description of HCl.

We can write down another wavefunction which goes to the ionic extreme, and has both electrons on the chlorine atom, i.e. representing the H⁺Cl^– structure. In this wavefunction, Y_ion, both electrons are in the chlorine 3p_z orbital.

Both of these wavefunctions, Y_cov and Y_ion, give only a partial description of the bonding in HCl, each representing one extreme. A better overall description - a better wavefunction- is given by combining the two:

Y = c_covY_cov + c_ionY_ion

The coefficients c_cov and c_ion are numbers which give the relative contribution of the ionic and covalent forms.

The variation principle tells us that the best wavefunction (of this sort) is the one with the lowest energy.

This means we can find the best wavefunction by varying the coefficients until we find the wavefunction which has the lowest energy - this is the variational method.

We might find, for example, that the best wavefunction at a particular internuclear distance is

y = 0.3 y_cov + 0.95 y_ion

(indicating that the ionic form plays a bigger role than the covalent form).

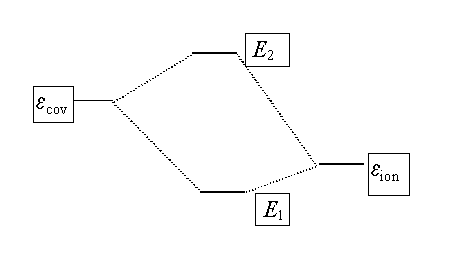
The energy of the better wavefunction resulting from a combination of the original wavefunctions is lower than the energies of either of the original wavefunctions.

The values of the coefficients is found by minimizing the energy with respect to them - the variational method.

The variational method is the most important way of finding molecular wavefunctions.

Molecular Orbitals and the Linear Combination of Atomic Orbitals (LCAO) Approximation