If we multiply out the secular determinant we obtain:

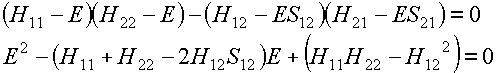(16)

which you should now be able to recognise as a quadratic equation for E. It has two solutions E₁ and E₂. These are the two molecular orbital energies.

We now take one of these, E₁ , and place it in the secular equations (eq. 14). These equations now have a nontrivial solution and we find the ratio c₂/c₁ by solving them. The absolute value of the coefficients c₁ and c₂ can only be found by using the normalization condition:

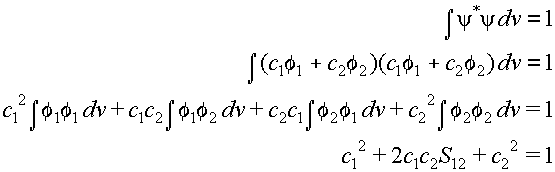(17)

We now add an extra index to the coefficients c₁ and c₂ to show that they belong to molecular orbital no. 1. We obtain the coefficients for molecular orbital No. 2 in the same way by substituting the second solution of the secular equations, E₂ , into the secular equations.

Molecular orbital no. 1

Molecular orbital energy: E₁

Molecular orbital:

Molecular orbital no. 2

Molecular orbital energy: E₂

Molecular orbital:

Lecture 2