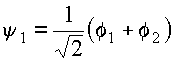The Hückel secular determinant for ethene is:

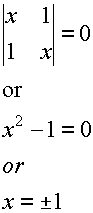
Therefore E=a + b (x = –1) or E=a – b (x = 1).

For the lower energy E₁=a + b (x = –1) we substitute into the secular equations (eq. 6):

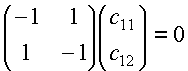
This gives c₁₁=c₁₂

y₁ = c₁₁ ( f₁ + f₂ )

The normalization condition is:

Therefore:

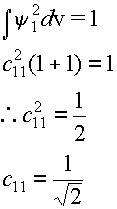
Summary: the Hückel MOs of ethene