Finding the p molecular orbitals of ethane using the LCAO approximation

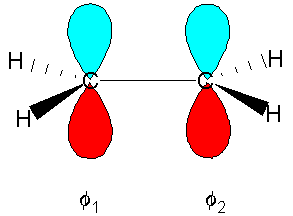
The expression for the energy can be written as:

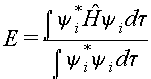
where the integrals are over all space. The energy calculated in this manner will depend on the coefficients c_i1, and c_i2,

The variational principle states that if an approximate wavefunction (such as this) is used to calculate the energy, the value obtained for the energy is always greater than or equal to the exact ground state energy of the system, i.e.

E ³ E_exact

So the next stage in this case is to minimize the energy with respect to the c_ip,, i.e, c_i1 and c_i2. This minimized energy will still be above the true ground state energy. The wavefunction with the values of c_i1 and c_i2 that give the minimum energy is the best wavefunction it is possible to obtain using just a simple combination of two atomic orbitals. It gives the energy closest to the exact ground state energy.

As we have seen in the previous lecture this leads to secular equations and the secular determinant:

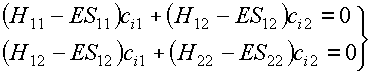
We can write them in matrix form:

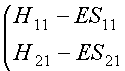
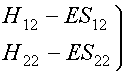
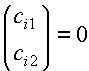(2)

The trivial solution of these is c_i1 = c_i2 = 0. (Why is this of no interest?)

Next: the secular determinant and the energies of the molecular orbitals of ethene