Bond stretching

As you know, a useful function for modelling typical potential energy curves for bond stretching is the Morse potential. This is usually not used in molecular mechanics (it involves 3 parameters for every bond, and is also time-consuming to calculate). Instead, the simpler harmonic form (above) is used, requiring two parameters (the force constant, and the reference bond length l₀). With the harmonic form, the energy of bond stretching can be calculated quickly, and the behaviour close to the minimum is given reasonably well. However, modelling bonds as springs means that they can't dissociate - this is one of the reasons that standard molecular mechanics methods cannot be used to model chemical reactions. Typical values of force constants are of the order of several hundred kcal mol^-1Å^-2.

Angle bending

The energy bending of valence angles is also calculated using a harmonic term. Less energy is needed to distort an angle away from its equilibrium value, so force constants for angle bending are smaller.

Rotation around bonds: torsion angle energy

Torsion terms are very important in determining the structure of 'organic' type molecules. The energy for rotation of torsions are represented by series of cosine functions, i.e. the energy for a torsion angle w is given by:

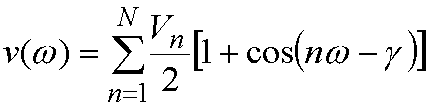(2)

Typically 1-3 cosine terms will be used for every torsion. V_n is often called the barrier height, but this is not a very good description - it can even take negative values - and each torsion may be associated with several V_n. Also, other terms (e.g. non-bonded 1-4 interactions) will contribute to the barrier height. n is the multiplicity, giving the number of minima as the torsion is rotated through 360º. g is the phase factor - this gives where the cosine function has its minimum.

'Improper' torsions

These are needed, for example, to keep the 3 atoms bonded to an sp² carbon in the same plane. Molecular mechanics potential function do not include the effects of p-bonding, for example, and so to model a carbonyl group correctly, an additional improper torsion term is needed. This is described as an improper torsion because the atoms involved are not bonded together in the normal A-B-C-D order.

For example, for the carbonyl fragment shown, an improper torsion could be defined as 1-4-3-2.

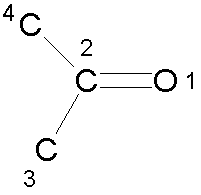
A cosine potential is then used to restrain the improper torsion angle to 0º or 180º:

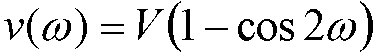(3)

Cross terms

In reality, individual bond stretches, angle bends and torsion twists are not independent of one another. For example, as a valence angle bends, the bonds involved are likely to change at the same time. Another example is shown in this figure:

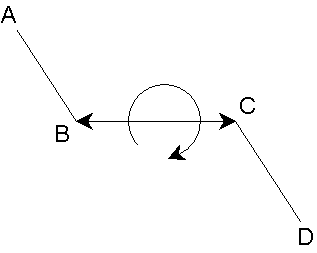
With rotation around the bond, the bond should lengthen, (stretching of the bond leads to a reduction in the barrier, facilitating rotation around the bond). This could be represented by a stretch-torsion cross term (for the bond length, l (e.g. B-C in the figure), and the torsion angle w (e.g. A-B-C-D in the figure):

To represent the coupling between angle bending and bond stretching, Urey-Bradley terms may be used, effectively applying a harmonic restraint on the distance, r, between atoms 1,3 with respect to each other.

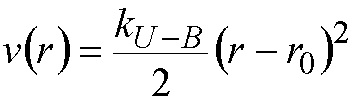
Non-bonded Interactions

Van der Waals and electrostatic forces play vital roles in determining the structures of molecules, and their interactions. Electrostatic forces act over large distances. Non-bonded interactions play an important role not only in the interaction of separate molecules, but also within molecules.

van der Waals interactions

Deviations from ideal gas behaviour (e.g. in noble gases) were studied in detail by van der Waals, and so the interactions giving rise to these deviations (not due to the effects of electrostatics) are referred to as van der Waals interactions. These can be thought of as being made up of an attractive (longer range) and a (short range) repulsive component. The attractive contribution is due to dispersion forces, created by instantaneous fluctuations in electronic distribution, giving rise to an instantaneous dipole in a molecule or atom, which in turn creates a dipole in neighbouring molecules or atoms. Dispersion interactions were analysed in the early days of molecular quantum mechanics by London, and so are sometimes referred to as London forces.

Next: more on non-bonded interactions