‘Ab initio’ Molecular Orbital Calculations

The electronic energy of a molecule can be calculated by treating the overall electronic wavefunction as being a product of molecular orbitals (strictly as a Slater determinant of molecular orbitals to satisfy the Pauli principle; we should also include the electron spin).

So we can write a molecular wavefunction as:

Y = y₁y₂y₃y₄…y_n (27)

Each molecular orbital, y_i, is written as a linear combination of atomic orbitals (the familiar LCAO approximation):

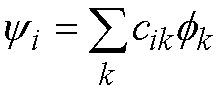(28)

The molecular orbitals can be found by the Hartree-Fock method. The Hamiltonian operator contains terms for the potential and kinetic energy of the electrons. It includes the interactions between the nuclei and the electrons, and the electron-electron repulsion. The molecular orbitals are found by making an initial guess at the coefficients. Then the determinant

½H–ES½= 0 (29)

H contains the Hamiltonian matrix elements, and S the overlap matrix elements. Solving this determinant gives the molecular orbital energies E, which are substituted into the secular equations to give new values of the coefficients c_i. This whole process is repeated until the coefficients do not change from one cycle to the next. The orbitals are then described as self-consistent, and this process as a self-consistent field procedure.

Each molecular orbital is made up of a combination of atomic orbitals:

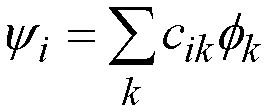(28)

The set of atomic orbitals (f_k) used is called a basis set. When one function is used for each filled atomic orbital (e.g. using 1s, 2s and 2p orbitals for a carbon atom, this basis set is called a minimal basis. Using more functions than this will improve the calculation – it will increase the flexibility and quality of the overall wavefunction. From the variational principle we know that a better wavefunction will give a lower energy. The bigger the basis set, the better the calculation. If a very large number of functions – a very large basis set – is used to represent the atomic orbitals, we approach the Hartree-Fock limiting energy: the lowest energy (best molecular wavefunction) that can be achieved by the Hartree-Fock method.

Correlation energy