Molecular Mechanics
Empirical Potential Functions
Ideally, we would like to model molecules using quantum mechanical methods, to calculate the electronic properties of the molecule. However, quantum mechanical methods are very demanding of computer time and memory. Many interesting molecular systems are simply too large for quantum mechanical calculations to be practical.
Instead, can get useful results for many properties (e.g. molecular
structure) from simpler methods which do not include the electrons – ‘molecular
mechanics’ methods. The molecular potential energy is calculated as a function
of the nuclear (atomic) positions. The total potential energy is the sum of
several contributions, each representing a particular type of interaction in
the molecule (e.g. for stretching of chemical bonds).
As mentioned above, a typical molecular
mechanics potential function (or ‘force
field’) is:
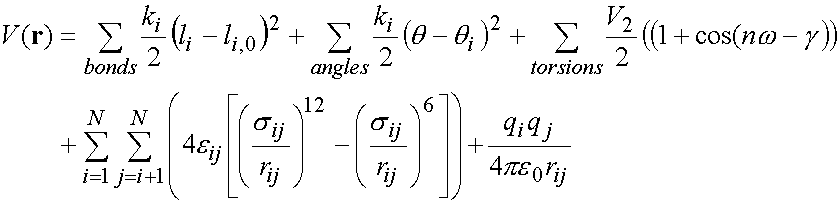 (1)
(1)
·
The first term models bond
stretching (here represented by a harmonic potential for each bond, with force
constant ki/2 and reference length l0),
with the sum over all bonded atom pairs in the molecule.
·
The second term
represents valence angle bending (i.e. for angles X-Y-Z, in which X and Z are
both bonded to Y), again as a harmonic potential here, summing over all valence
angles in the molecule.
·
The third term represents the
energy of rotation around torsion angles.
·
The remaining terms represent the non-bonded
interactions (here represented by a Lennard-Jones potential for van der Waals
interactions, and a Coulomb term for electrostatic interactions (here between
atoms i and j, with atomic partial charges qi
and qj). Non-bonded
interactions are calculated between atoms in different molecules, and between
atoms in the same molecule separated by at least 3 bonds.