For the Newton-Raphson step, we need the Hessian, the matrix of second derivatives of the function,

i.e. for our 2-dimensional function, a 2´2 matrix:

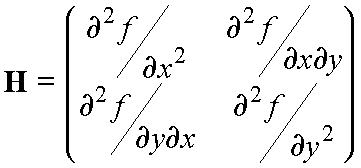
For f(x,y)=x² + 3y²,

d²f/dx² = 2;

d²f/dy² = 6;

d²f/dxdy = 0,

so:

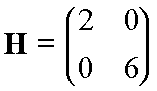
and the inverse matrix is

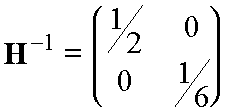
The gradient is (df/dx = 2x ; df/dy = 6y):

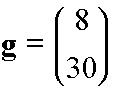
for (x,y)= (4,5)

So the new coordinates are

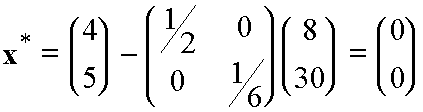
The minimum is the point x=0, y=0.

For a purely quadratic function like this one, the Newton-Raphson method finds the minimum in a single step from any point on the surface.

Check this is true for the function f(x,y) = 2x² + 2y^2..

Next: features of the Newton-Raphson method