Energy levels of a harmonic oscillator
Remember that for a harmonic
oscillator, solving the Schrödinger equation gives energy levels
Ev=(v+1/2)hn v=0,
1, 2…..
(1)
This shows that an oscillator like this
cannot be at rest - the minimum vibrational energy it can have is hn/2 - the
zero-point energy.
The frequency, n, is related to the force constant, k, for the vibration:
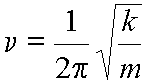 (2)
(2)
The force constant, k, is given by the second derivative of
the potential energy, which in one dimension is k=(d2V/dx2).