The mass-weighted Hessian matrix is:
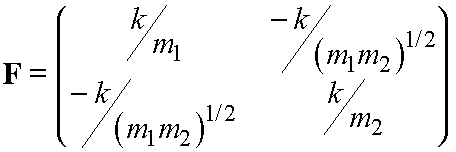 (8)
(8)
To find the eigenvalues, the secular determinant is solved:
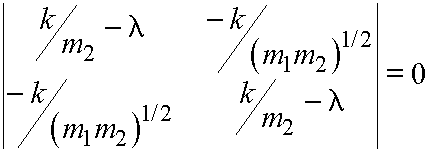 (9)
(9)
This gives
a quadratic equation, with solutions
l1=0
and
l2=k/m (where the reduced mass m = m1m2/(m1
+ m2)).
The solution l = 0 corresponds to a translation (in
the x direction, the only coordinate
we are considering here).
The solution l = k/m gives the frequency of the vibration - from equation (5) above,
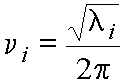
Therefore
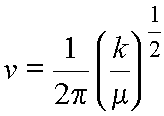 (10)
(10)
as expected for a harmonic oscillator.