Molecular simulations

· The examples above include only one structure to represent each molecule (an energy minimum or transition state structure).

· This can be OK for small molecules where a single conformation predominates.

· At best, ab initio calculations could include several conformations of a molecule, resulting from a number of geometry optimizations.

· However, with larger molecules, many different conformations may need to be considered.

· Also, of course, we are often interested in molecules in condensed phases, e.g. in solution, in solids, at surfaces, etc. Macroscopic systems of this sort contain huge numbers of atoms (e.g. solvent molecules), so the number of energy minima (and transition states) will be vast.

· For modelling condensed phase systems, we really need to use molecular simulations. These examine the structure and properties of large numbers of atoms, and different configurations of these systems.

· We will consider three molecular simulation techniques: lattice dynamics, molecular dynamics and Monte Carlo.

Lattice dynamics

· Useful for periodic solids (e.g. MgO, MnO, CaO, MgSiO₃…).

· Empirical potential functions, including electrostatic interactions, and e.g. Buckingham potential (see under discussion of van der Waals interactions above) for nonbonded interactions are used

· Based on calculation of normal modes, and associated partition functions. Vibrations in the sold state are called phonons.

In lattice dynamics, calculate Helmholtz free energy of a structure:

A = U – TS

(i.e. constant volume equivalent of Gibbs free energy G = H – TS).

A has components due to stattic lattice energy (U_stat) and to the vibrations:

A = U_stat + U_vib – TS

· Need vibrational frequencies for Uvib and S – these are found from the vibrational partition functions.

· There is one partition function for each normal mode.

· Strictly, need to use all normal modes, but in practice, only a subset is used

· As above, each normal mode gives rise to a partition function:

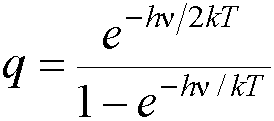
The Helmholtz free energy can be found from the partition function

A = -kT ln q (see Atkins, 6th edn. Pg. 594)

So the total vibrational energy at a particular temperature, T, is given by

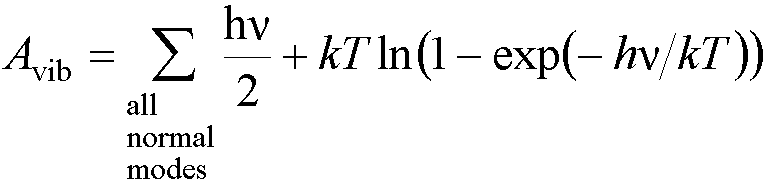
(U_stat is then added to A_vib to give A).

· All other thermodynamic properties can then be found,

· e.g. the entropy is found from –S = .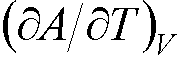

· Lattice dynamics can be used to compare relative stabilities of different types of structure, and the variation of stability with temperature or (particularly useful) pressure – e.g. comparing stability of NaCl and CsCl type of structures, for e.g. CaO. Can also calculate free energies, entropies and enthalpies of mixing.

· Also, lattice dynamics can be used to explain thermal expansion behaviour. Most substances expand on heating, but a few (e.g. ZrW₂O₈) contract. Negative thermal expansion happens in open structures, e.g. some silicates and zeolites. In these structures, expansion causes the frequencies of some vibrations to increase, making expansion entropically unfavourable e.g. transverse Zr-O-W vibrations (like a violin string).