Answers for example questions for Molecular Modelling

Dr. Adrian Mulholland

(1) What approximation leads to the concept of a potential energy surface? What types of points on a potential energy surface are particularly relevant in understanding a chemical reaction?

The Born-Oppenheimer Approximation allows the separation of electronic and nuclear motion, and so leads to the concept of a potential energy surface, i.e. the electronic energy can be calculated at a particular fixed nuclear geometry.

Two types of points are particularly relevant in understanding a chemical reaction. Firstly, minima correspond to stable molecular geometries (i.e. the structures of stable molecules). First-order saddlepoints are also useful. These points are an energy maximum in one direction, but a minimum in all other directions. A first-order saddlepoint corresponds to a transition state, i.e. the highest energy point along the reaction pathway. The energy difference between the minimum (corresponding to the reactants) and the transition state gives the (potential) energy barrier to the reaction.

(2) Two methods which are widely used for the optimization of molecular geometies are the ‘Steepest descents’ and ‘Newton-Raphson’ techniques. Without giving detailed mathematical descriptions, briefly outline the advantages and disadvantages of these two techniques.

The ‘steepest descents’ method of energy minimization is a simple and effective method of improving the geometry of a molecular model (i.e. finding a lower energy structure). It moves ‘straight downhill’ on the energy surface, taking steps in the direction of the negative of the gradient. This involves calculating the forces (gradients) on the atoms - the first derivative of the energy). The gradient is a vector (g), with one component for each coordinate. The step, s, is in the direction –g. The steepest descents step is determined mostly by the largest forces. It is therefore good for relieving strain in a built model. Only first derivatives are required - this is an advantage for large molecules. Steepest descents provides fast minimization (big steps) when far from minimum, but small steps (slow minimization) when close to minimum. It has slow convergence (i.e. it will find the minimum energy structure only very slowly). It may also oscillate around a minimum and never actually reach the minimum. Because it only moves ‘downhill’ on the energy surface, it is no use for TS searches.

The Newton-Raphson method uses in addition second derivatives of the energy and can be a better minimization method. It is efficient for small molecules, and converges quickly, in contrast to steepest descents minimization. However, it makes the approximation that the energy surface has a quadratic form, which is often poor approximation for molecular potential energy surfaces, particularly far from minimum The calculation, inversion and storage of the Hessian matrix (i.e. the matrix of second derivatives) is computationally difficult for large molecules. It is possible to locate stationary points other than minima on potential energy surfaces with the Newton-Raphson method, and this can be useful for transition state optimization. The Newton-Raphson method works well if the initial geometry is close to a stationary point, but may not work well if it is not. Also, technically the method may be difficult to use for some types of problem. Technical difficulties arise because of the need to calculate the Hessian, which is a potentially very large matrix (no. of variables squared). The calculation of the second derivatives can be demanding (requiring a lot of computer time), and their storage can be difficult (a lot of computer memory is required). The Hessian must be inverted (diagonalized), which is a technical problem for more than 1000 variables (1000 ´ 1000 matrix), i.e. approx. 300 atoms. It is possible to avoid calculating the Hessian matrix at every step by either using a guessed matrix (e.g. the identity matrix)or by using a Hessian update scheme (constructs an approximate Hessian based on e.g. the gradient and coordinates at current and new points. Calculating the Hessian at a lower level of theory can also reduce the demands of the calculation. When dealing with large numbers of atoms, though, the Newton-Raphson method is not suitable because of the large computational requirements. A first-order method has to be used instead (first-order methods use first derivatives of the energy; second-order methods use first and second derivatives).

(3) Give reasons why calculation and analysis of the harmonic vibrational frequencies of molecules may be useful. Outline the process involved in calculation of harmonic vibrational frequencies. In the case of a diatomic molecule, find the frequency of vibration (treat the molecule as a harmonic oscillator).

There are several reasons for calculating vibrational frequencies of molecules, including:

· To identify the nature of a stationary point found by geometry optimization (e.g. a minimum or a saddlepoint). At a minimum, all the 3N-6 eigenvalues of the Hessian are positive, so all the calculated frequencies will be positive.

· To calculate the infrared and Raman spectra of a molecule

· To calculate thermodynamic properties of a molecule

Vibrational frequencies are usually calculated by finding the normal modes of the molecule.

for a harmonic oscillator, solving the Schrödinger gives energy levels

E_v=(v+1/2)hn v=0, 1, 2….. (1)

This shows that an oscillator like this cannot be at rest - the minimum vibrational energy it can have is hn/2 - the zero-point energy.

The frequency, n, is related to the force constant, k, for the vibration:

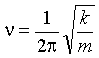(2)

The force constant, k, is given by the second derivative of the potential energy, which in one dimension is k=(d²V/dx²).

For a polyatomic molecule, the normal mode frequencies are found from the matrix of second derivatives (the Hessian matrix). It is important that the second derivatives are mass-weighted - this is to take into account the fact that a given force will different effects on atoms of different masses. For example, the zero-point energy is different for a proton than for a deuteron in the same type of bond, due to the difference in mass. Mass-weighting the Hessian takes care of these effects.

The mass-weighted Cartesian coordinates (x_m, y_m, z_m) of any atom are related to its Cartesian coordinates (x,y,z) by:

x_m = m^1/2x y_m = m^1/2y z_m = m^1/2x (3)

where m is the mass of the atom.

The mass-weighted Hessian matrix is given by:

F = M^–1/2HM^–1/2 (4)

M is a matrix containing the atomic masses. Like the Hessian matrix, H, it is a 3N ´ 3N matrix (N is the number of atoms). M is a diagonal matrix - the only non-zero elements are the masses.

Finding the eigenvalues (l_i) of the mass-weighted Hessian matrix, F, gives the frequencies of the normal modes, n_i:

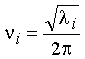(5)

If Cartesian coordinates are used, there will be 3N frequencies (from 3N eigenvalues), where N is the number of atoms. Among these frequencies, 6 will be very close to zero (5 for a linear molecule). These 6 correspond to overall translation and rotation of the molecule. The remaining 3N-6 are vibrations of the molecule.

Example of a normal mode calculation: finding the vibrational frequency of a diatomic molecule

The potential energy is taken here to be harmonic,

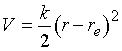(6)

where r is the separation of the two nuclei, and r_e their equilibrium separation. We can write this in terms of the Cartesian coordinates of the two atoms, x₁ (for atom 1) and x₂ (for atom 2) - we are taking the bond to lie along the x axis, and ignoring the y and z directions. Therefore, r = x₂-x₁. The second derivatives of the potential energy are: d²V/dx₁² = k, d2V/dx₂² = k, d²V/dx₁dx₂ = d²V/dx₂dx₁ = –k.

Therefore the Hessian matrix (for the x direction only here) is:

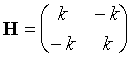(7)

The mass-weighted matrix is:

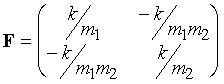(8)

To find the eigenvalues, the secular determinant is solved:

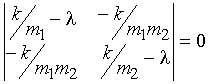(9)

This gives a quadratic equation, with solutions l₁=0 and l₂=k/m (where the reduced mass m = m₁m₂/(m₁ + m₂)). The solution l = 0 corresponds to a translation (in the x direction, the only coordinate we are considering here). The solution l = k/m gives the frequency of the vibration - from equation (5) above,

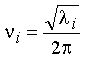
Therefore

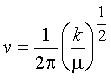(10)

as expected for a harmonic oscillator.

In general, calculations of vibrational frequencies (normal mode analyses) provide the frequencies themselves (as the square roots of the eigenvalues), but also the atomic displacements involved in each mode (from the eigenvectors), which tell us what each separate vibrational motion looks like. Typically a calculation will print out the frequency of each vibrational normal mode, and the associated atomic displacements.

(4) Outline techniques which could be used to generate models of transition state structures for chemical reactions. How could such transition state models be improved? Describe how you could confirm that a structure really is a transition state structure. Also outline how you could show that the transition state really is the right one for the reaction of interest.

For refinements of transition state structures, it is essential to have starting models which are close to the real transition state. Otherwise the optimization will probably not be successful. One way to generate a model of a transition state is to guess, using chemical knowledge and intuition (e.g. identifying which bonds are breaking in the TS, and so likely to be elongated). However, this is difficult to do well for large systems.

A better approach in general is coordinate driving (also called adiabatic mapping). This involves optimizing the structure of the system with a particular coordinate fixed. A sequence of optimizations is performed with the coordinate fixed at a given value for each optimization, then changed to a different fixed value for the next optimization. This can generate an energy profile, with the approximate TS at the highest point. For example, for ethane, optimizations could be carried out with the value of one H-C-C-H torsion angle changed in a series of steps from 60° to -60°. The energy would be a maximum for the structure optimized with the H-C-C-H angle equal to 0°, which would be the model for the TS structure.

If the structures of the reactant and product are known, can construct a model TS as a ‘midpoint’ between the two. For example, for the reaction H-N-C ® N-C-H, the TS model could be specified from the internal coordinates for the reactant and product. The H-N-C angle in the reactant is 180°, whereas it is 0° in the product. In the TS model, therefore, a value of H-N-C = 90° could be used as a first guess. The bond lengths (interatomic distances) could also be chosen to be intermediate between the reactant and product.

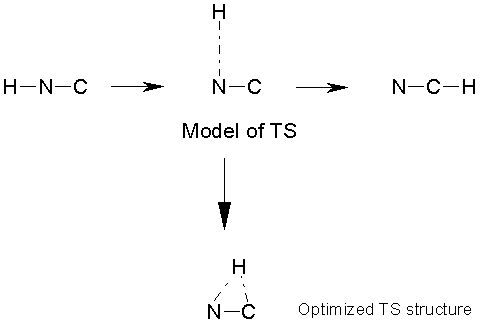
It is necessary to be careful in the choice of coordinates- trying to create a model TS with Cartesian coordinates would cause problems here (the hydrogen would end up between N and C!).

Alternatively, a TS model can be generated by performing a geometry optimization with a particular symmetry enforced - the TS may have a higher symmetry than the reactants or products. For example, the TS for the S_N2 reaction Cl^– +CH₃Cl ® CH₃Cl +Cl^– has D_3h symmetry (the two C-Cl distances will be the same, and the H atoms all lie in a plane):

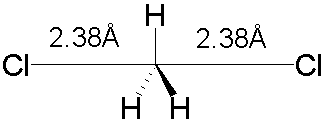
There is no single technique which can be guaranteed to give a good TS model for all reactions. Finding a good model may be a matter of trial and error. A bad model will not optimize to the correct TS.

To check that the structure resulting from a geometry optimization really is a transition state structure, a normal mode analysis (calculation of vibrational frequencies) can be performed. For a transition state structure (saddlepoint), one of the eigenvalues of the Hessian will be negative - i.e. the structure is a maximum in one direction. The frequency is given by the square root of the eigenvalue, so formally there will be one imaginary frequency. If there is one, and only one, imaginary frequency, the structure really is a transition state.

In contrast, a minimum energy structure will have all positive frequencies (at a minimum, all the 3N-6 eigenvalues of the Hessian are positive, so all the calculated frequencies will be positive). If there is more than one imaginary frequency, the structure is a higher order saddlepoint (a maximum in more than one direction), and chemically not very interesting - you would need to do more geometry optimization to find a real TS structure.

It is still possible, however, that the TS structure found by a geometry optimization is the TS for a process different to the one of interest. To check that the TS structure really is the desired TS, examining the atomic displacements for the reaction coordinate can show which atoms are involved (the atomic displacements for the imaginary frequency are very important - this normal mode corresponds to motion along the reaction coordinate). To prove that it really is the desired TS, calculating the steepest descents path from the TS should produce (in one direction) the reactants and (and in the other direction) the products. This path calculated in mass-weighted coordinates from the TS is called the intrinsic reaction coordinate.

(5) Find the Newton-Raphson step, and the minimum, for the function f(x,y) = 2x² + 2y², starting from the point (x,y) = (3,–2). Show your working.

The Newton-Raphson expression for stepping towards a minimum for a multidimensional function is

x_k+1 = x_k – gH^–1

For a molecule with N atoms, there are 3N Cartesian coordinates, so the gradient is a vector g (as above), with 3N terms (dV/dx_i).

The second derivatives have the form (d²V/dx_idx_j), involving each coordinate, and so make up a 3N´3N matrix, called the Hessian matrix, H.

The energy of a particular molecule can be given as a function of two coordinates:

E(x,y) = 2x² + 2y²

Find the Hessian and inverse Hessian matrices for this system.

The Hessian, the matrix of second derivatives of the function, i.e. for this 2-dimensional function, a 2´2 matrix:

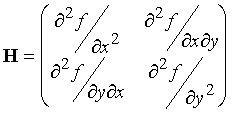
For f(x,y)=x² + 2y², d²f/dx² = 2; d²f/dy² = 4; d²f/dxdy = 0, so:

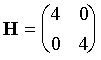
and the inverse matrix is

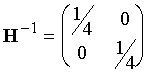
Give the value of the Newton-Raphson step for (x,y) = (3,–2) and give the predicted coordinates of the minimum of the function.

The gradient is (df/dx = 4x ; df/dy = 4y):

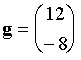for (x,y)= (3,–2)

So the new coordinates are

The minimum is the point x=0, y=0. For a purely quadratic function like this one, the Newton-Raphson method finds the minimum in a single step from any point on the surface.

(6) Briefly describe the following methods for calculating molecular energies and geometries (outline their advantages and disadvantages):

(i) ab initio molecular orbital methods

(ii) semiempirical molecular orbital methods

(iii) molecular mechanics methods

(iv) combined quantum mechanics/molecular mechanics methods

(i) Ab initio molecular orbital calculations can provide accurate geometries and energies, if a high enough level of theory is used. In many cases, using a large basis set and a method which includes electron correlation can provide good answers. However, such calculations are extremely demanding of computational resources, and so are feasible only for small molecules. The most basic form of ab initio calculations use the Hartree-Fock method. These can be performed reasonably quickly, even on fairly large molecules (with e.g. 10-100 heavy atoms). Hartree-Fock calculations can be useful for determining geometries of stable molecules. The best results are achieved with large basis sets. However, they do not include electron correlation, and so they do not provide a good description of chemical reactions (they deal poorly with situations where bonds are partially formed or broken).

(ii) Semiempirical Methods Ab initio calculations require a lot of computer time and memory. This is because many difficult integrals involving the atomic orbitals have to be calculated for the electron-electron interactions. So-called ‘semiempirical methods’ are much faster, and can be applied to bigger molecules (e.g. 100s of atoms instead of 10s of atoms). In semiempirical methods, fewer integrals have to be calculated because simplifying approximations are made. The integrals that do remain are not calculated directly, but instead are replaced by simple functions. These simple functions are parameterized so that the semiempirical method reproduces experimental data (e.g. molecular structures, dipole moments, ionization energies, etc.) as well as possible. The experimental data contain the effects of electron correlation, and so semiempirical methods can be a good choice in some cases.

However, the approximations used make them often somewhat inaccurate. Also, they can only reproduce properties of molecules similar to those used in parameterizing the method. Usually only data for stable molecules are included, which means that transition states may not be dealt with well. Examples of semiempirical molecular orbital methods include MNDO, AM1 and PM3.

(iii) Molecular mechanics. Even faster (‘cheaper’) calculations of the structures and energies of molecules are possible using ‘molecular mechanics’. These methods forget about electrons and nuclei, and treat atoms as point charges with van der Waals radii. Bonds are treated as springs (simple harmonic energy terms), with simple terms also for torsion angles and bond angles. These functions contain parameters (bond lengths, force constants, etc.) which are optimized to reproduce the structures of molecules as found experimentally or by ab initio calculations.

E_MM = E_bond + E_angle + E_torsion + E_VDW + E_{electrostatic}

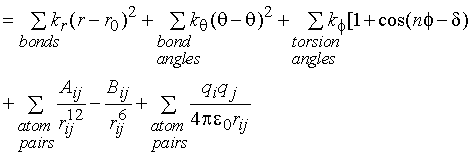
With molecular mechanics methods, it is possible to study very large molecules (solids, polymers, surfaces, proteins, DNA, etc.). The motion of these molecules can be studied using molecular mechanics energy functions in molecular dynamics simulations. However, molecular mechanics potential functions are not suitable for modeling chemical reactions. The functional form is incorrect (e.g. a harmonic term for stretching a bond does not allow the bond to break); also the use of stable molecules in the parameterization process means that only stable molecules can be described by these functions, and not e.g. transition states.

(iv) Combined quantum mechanical/molecular mechanical (QM/MM) methods. To treat a chemical reaction, a quantum mechanical method is required to describe the breaking and forming of bonds - such methods include ab initio and semiempriical molecular orbital methods. Molecular mechanics methods are not suitable, as outlined above. However, ab initio methods cannot be applied to systems with more than a few tens of atoms, because the computational demands are too great. Semiempirical methods can be applied to bigger systems (100s of atoms), but even they are too demanding for calculations on very large systems. For calculations on reactions in solution, where thousands of solvent molecules may need to be included, or for reactions in solids, at surfaces or in biological macromolecules (e.g. enzymes), a different approach must be used.

Quantum mechanical/molecular mechanical (QM/MM) methods allow reactions in large systems to be studied. A small region including the reacting atoms is treated with a QM method (e.g. ab initio molecular orbital theory), while most of the system is represented more simply by molecular mechanics. The reacting region ‘feels’ the influence of the molecular mechanics environment - for example, the atomic charges of the MM atoms affect the QM atoms. By combining the accuracy of a QM method (for a small reacting system) with the speed of a MM method (for its surroundings), reactions in large molecules and in solution can be studied.

Schematic representation of the setup of a QM/MM calculation. A small region containing the reacting atoms is treated by a quantum mechanical method (e.g. by molecular orbital theory), while its surroundings are represented more simply by molecular mechanics.

(7) What is meant by the term ‘correlation energy’? What methods can be used to calculate energies including correlation effects?

Correlation energy

The Hartree-Fock method has important limitations. Even the Hartree-Fock limiting energy is above the true energy of a molecule. This is because correlation energy is not included. The correlation energy can be defined as:

E_correlation = E_true – E_Hartree-Fock (30)

This error arises because the interaction of one electron with another is treated as the interaction with a smoothed out, averaged electron density. In fact, the position of one electron affects the position of the other electron, because they repel one another. If one is on one side of the molecule, the other electron is likely to be on the other side. Their positions are correlated, an effect not included in a Hartree-Fock calculation.

While the absolute energies calculated by the Hartree-Fock method are too high, relative energies may still be useful. If the correlation energy does not change during a process, the energy calculated for the process with the Hartree-Fock method will be close to the real value. The correlation energy does not change very much if the bonding in the molecule does not change much. So, for example, calculations of conformational properties can be done accurately at the Hartree-Fock level (e.g. calculating the rotational barrier in ethane). When the bonding in a molecule changes, though, the correlation energy changes significantly. This means that the Hartree-Fock method performs very poorly for calculations on breaking chemical bonds. The dissociation energy predicted is too high, and it may predict the wrong products to be formed (e.g. predicting the formation of ions when in fact neutral atoms should be formed by breaking a bond).

For treating chemical reactions, we need to use methods which include electron correlation. Many methods of this type use a Hartree-Fock calculation as a starting point. An example is the use of perturbation theory, developed by Møller and Plesset and available in many ab initio molecular orbital programs. The term MP2 is used for second-order perturbation theory (the results given above for the Diels-Alder, S_N2 and Claisen rearrangement reactions were calculated at the MP2 level). A more sophisticated (and computationally demanding) approach is called configuration interaction (CI). In this technique, different electronic configurations are allowed to interact, to give a better overall wavefunction. The improved, configuration interaction, molecular wavefunction is written as a linear combination:

Y_{improved, CI} = aY₀ + bY₁ + cY₂ + ….

Y₀ is the wavefunction found first (e.g. from a Hartree-Fock calculation). Y₁, Y₂ etc. are wavefunctions based on the original Y₀ in which some electrons have been moved into higher energy molecular orbitals which are unoccupied in Y₀. This gives a better overall wavefunction, Y_{improved, CI}. CI calculations tend to be extremely demanding of computer resources, because many excited electronic configurations (Y₁, Y₂…) are possible. Usually only a limited number can be included.

Recently, techniques based on density-functional theory have become popular. The energy of the molecule is calculated as a function (strictly a functional) of the electron density. Density-functional theory calculations on molecules usually include a Hartree-Fock calculation. They are popular because they include electron correlation, but are not as demanding of computer resources as methods such as MP2 and CI.

(8) The Claisen rearrangement of allyl vinyl ether to form 5-hexenal is found to have an activation enthalpy, DH^‡, of 92.5 kJ mol^-1 and an activation entropy DS^‡ of –0.038 kJ mol^-1 K^-1. Calculate the first-order rate constant of this reaction at 300K.

At 300K, the activation free energy for the reaction is given by:

D^‡G = D^‡H – TD^‡S

D^‡G = 92.5 – (300 ´ –0.038)

D^‡G = 92.5 + 11.4 = 103.9 kJ mol^-1

A (first-order) rate constant can be calculated from

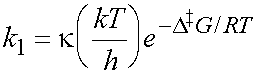
k is the transmission coefficient. For most reactions, k is close to 1, so we can put k = 1 here (use this approximation generally, unless a specific, different value of k is given).

(kT/h) = (1.380 ´ 10^-23 ´ 300) / (6.626 ´ 10^-34) = 6.2 ´ 10¹² s^-1

exp (–103,900/ (8.315 ´ 300) = exp –41.65 = 8.159 ´ 10^-19

(be careful to use Joules (not kJ) for D^‡G, as R = 8.134 J K^-1 mol^-1).

So the rate constant for the reaction is 8.159 ´ 10^-19 ´ 6.2 ´ 10¹² s^-1 = 5.1 ´ 10^-6 s^-1

(9) The enzyme citrate synthase catalyses the formation of citrate, the first step in the central metabolic pathway, the citric acid (or Krebs) cycle. The enzyme is found to have a maximum turnover number (see e.g. Atkins, ‘The Elements of Physical Chemistry, (3rd ed.) pg. 252) of 100s^-1 at 298K. What is the activation free energy for the enzyme-catalysed reaction at this temperature?

The maximum turnover number can be treated as an effective first-order rate constant (from the Michaelis-Menten mechanism for enzyme action).

It can therefore be expressed as

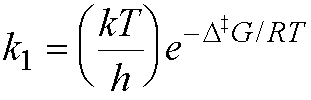
Therefore, the activation free energy is given by:

D^‡G = RT ln (hk₁/kT)

= – 8.314 ´ 298 ln (100/6.2 ´ 10¹²)

= - 8.314 ´ 298 ´ -24.85

= 61569 J mol^-1

= 61.6 kJ mol^-1

Exam question from 2003:

Answer part (a) or part (b)

(a) Give an expression for a ‘molecular mechanics’ potential energy function of the type used for standard macromolecular simulations. Include intra- and intermolecular terms. State clearly what each energy term represents, and its physical origin. How, typically, would the parameters of such a potential energy function be found? Discuss the range of applicability of a potential energy function of this type, its strengths and its limitations. Give brief examples of applications. What improvements could be made to a potential energy function of this type?

The molecular mechanics potential functions discussed in the course have the general form:

E_MM = E_bond + E_angle + E_torsion + E_VDW + E_{electrostatic}

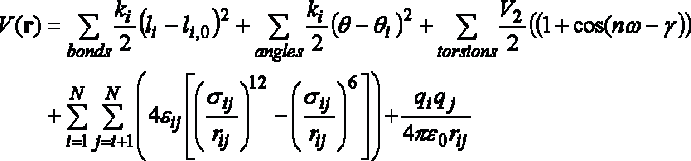
The answer should discuss the harmonic function used to model bond stretching, why this is chosen over e.g. a Morse potential, the limitations of the harmonic potential (e.g. no dissociation; poor behaviour away from minimum); the harmonic valence angle bending; the cosine series for torsion angles, mentioning in each case the meaning of the symbols (i.e. force constants, barrier heights, phase factors). The possibility of bonded cross terms (e.g. stretch-bend coupling) should be outlined, together with possible functional forms (e.g. Urey-Bradley 1-3 terms). The final terms should be identified as the non-bonded interactions in the potential function, van der Waals and electrostatic terms. The answer should discuss which non-bonded interactions would be calculated (i.e. 1-4 interactions etc). In discussing the van der Waals terms, the repulsive and attractive interactions should be identified, and the cause (dispersion interactions and exchange repulsion) should be outlined. Atomic partial charges should be described, with typical values (e.g. relating to electronegativity), and the ability of these models to reproduce hydrogen bond structures. Limitations of molecular mechanics force fields such as lack of electronic polarizability (fixed atomic charges), inability to model reactions (incorrect functional form), dependence on parameterization (e.g. limited dataset), should be discussed. Practical improvements include: inclusion of atomic polarizability (simple models should be given), different forms for bonding interactions; and combined quantum mechanics/molecular mechanics (outline briefly) - allow modelling of reactions.

(b) Discuss the Monte Carlo and molecular dynamics simulation methods. Outline the techniques by which each is carried out. Compare and contrast the two techniques. Briefly also discuss the lattice dynamics technique.

Describe basic features of MD and MC. Outline integration algorithms for MD, typical timesteps, use of SHAKE algorithm for increasing timestep. For MC, outline importance sampling, Metropolis method, random number generation, Monte Carlo 'moves'. Sampling efficiency. Classical MD determines atomic positions through solving Newton's equations of motion. Differences between MC and MD: e.g. MD gives information on time dependence of properties, MC does not. MD has a kinetic energy contribution to the total energy, whereas MC only includes potential energy. Standard MD would be performed in the NVE ensemble, MC would be performed in canonical ensemble (N,V,T) (although both methods can be modified to sample from other ensembles). Definition of temperature in MD. Lattice dynamics - brief outline of methods. Calculation of free energies through lattice dynamics - normal mode analysis, calculation of free energy, enthalpy and entropy through consideration of harmonic vibrational frequencies and partition functions.