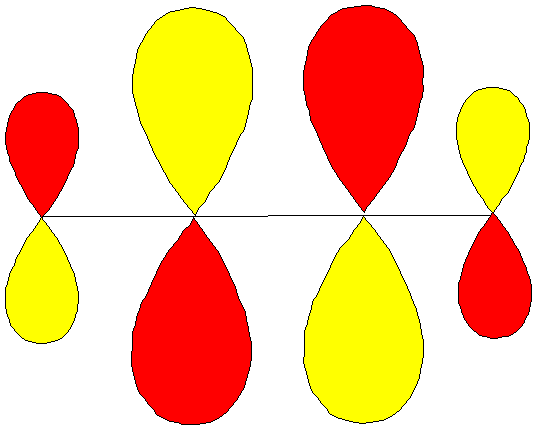
The Hückel p molecular orbitals of 1,3-butadiene

What do the orbitals look like?

(Atkins pg. 436)

· Draw the orbitals using the coefficients c1, c2, c3 and c4 for each molecular orbital in turn.

· Both the sign and the size of the coefficient for each atomic (2p) orbital are important

· Diagrams here drawn to emphasize nodes (sign changes), size isn’t important for this

y₁ -- lowest energy p M.O. (E = a + 1.62b)

-- no nodes other than in molecular plane:

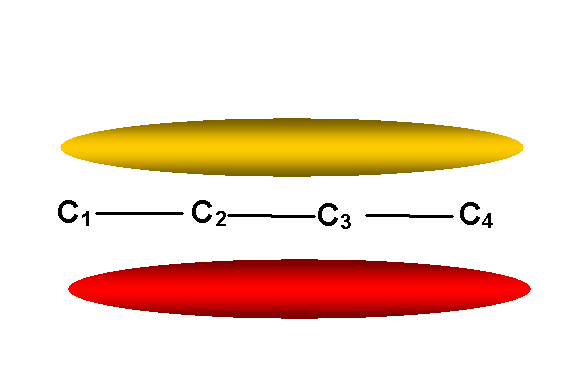
y₁ = 0.37f₁ + 0.6f₂ + 0.6f₃ + 0.37f₄

_______________________________________________

y₂ -- second lowest energy p MO (E = a + 0.62b)

-- one node other than in molecular plane:

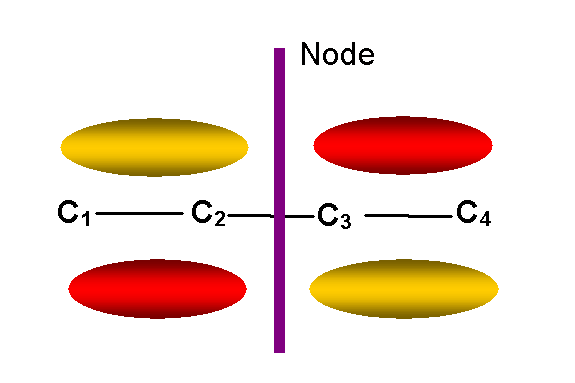
y₂ = 0.6f₁ + 0.37f₂ – 0.37f₃ – 0.6f₄

_______________________________________________

y₃ -- first unoccupied antibonding p MO (E = a – 0.62b)

-- two nodes other than in molecular plane:

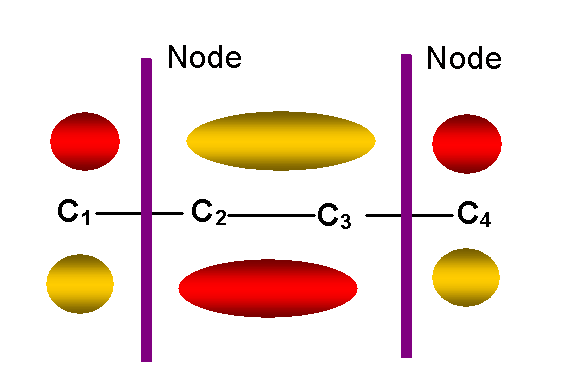
y₃ = 0.6f₁ – 0.37f₂ – 0.37f₃ + 0.6f₄

_______________________________________________

y₄ -- highest antibonding p MO (E = a – 1.62b)

-- 3 nodes other than in molecular plane:

y₄ = 0.37f₁ – 0.6f₂ + 0.6f₃ + 0.37f₄

Or, when size matters:

General conclusions about MOs