ENERGY QUANTISATION
- Any atom or molecule can ONLY HAVE CERTAIN
FIXED ENERGIES, energy is QUANTISED and an atom or molecule can
exist only in certain discrete levels.
 This is totally unlike our everyday experience!
This is totally unlike our everyday experience!
In many ways electrons, atoms and molecules behave like nothing like we might expect!
e.g., a vibrating molecule oscillates like a pendulum,
- There are 1012
oscillations per second, i.e., the frequency of vibration is 1012
s-1
- The molecule has vibrational energy and quantum
chemistry tells us the molecule can ONLY have vibrational energy,
hn/2, 3hn/2, 5hn/2
where n ("nu") is the frequency of vibration and h is Planck's constant (approx. 6.6 x 10-34 J s).
So in this case the allowed energies are:
3.3 x 10-22 J, 9.9 x 10-22 J, 16.5 x 10-22 J.....
- NOTE: Because the minimum energy is ½hn the molecule is always vibrating. It is never at rest! It has ZERO-POINT energy, which must be allowed for in many applications.
MOLECULAR ENERGY LEVELS
Molecules can exist only in certain discrete energy states.
- Why is energy quantization important? Becauseof the link between the energy levels and the spectra observed experimentally.
SPECTROSCOPY AND ENERGY LEVELS
The difference in energy between any two different energy levels determines the frequency of light absorbed when there is a transition between the two levels.
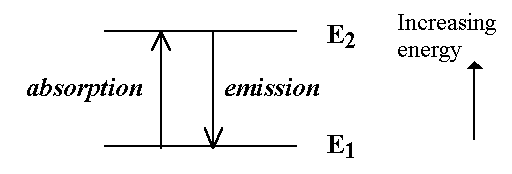
- The Bohr-Einstein condition is:
DE = E2 - E1 = hn eq. (1.1)
where n ("nu") is the frequency of the light absorbed/emitted
and h is Planck's constant. hn is a quantum ("packet") of energy - called a photon.
If have many energy levels get many transitions - hence get SPECTRUM characteristic of the atom or molecule studied (molecular "fingerprint").
Since light is so central to chemistry we now consider light in more detail.
LIGHT
- Exhibits both wave and particle
properties! This wave-particle "duality" is a feature
of the quantum world.
Light as a Wave:
- Light consists of an oscillating electric field and an oscillating magnetic field that travels through space with speed c (2.998 x 108m s-1 in vacuum).
- Often also encounter the wavenumber
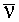
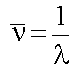 eq.(1.2)
eq.(1.2)
Units of  are m-1,
though usually quoted in cm-1.
are m-1,
though usually quoted in cm-1.
Example: Street lights are yellow due to emission from excited Na atoms: in fact
have 2 spectral lines centred on
l = 589.3 nm = 589.3 x 10-9
m
Find n and 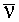 .
.
n = c / l = 5.09 x 1014 s-1
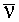 = 1 / l = 1,697,000 m-1 = 16,970 cm-1.
= 1 / l = 1,697,000 m-1 = 16,970 cm-1.
Light as particle:
- Sometimes, though, light behaves as if it was a stream of particles. (e.g., eq. (1.1))
- E.g., the photoelectric effect (basis of photoelectron spectroscopy)
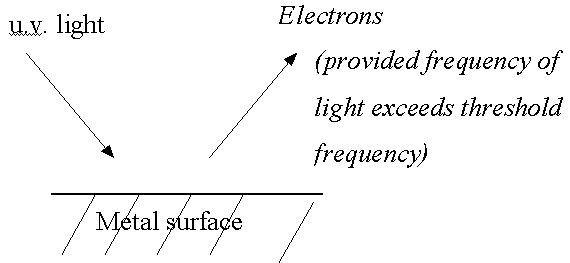
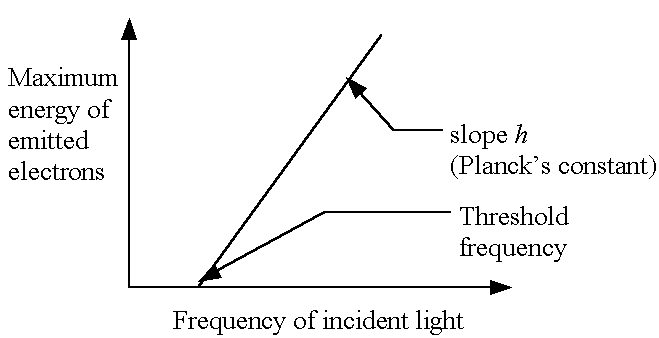
See handout
- Light as wave and particle
Also: (!)
- Electrons and atoms also behave like particles and waves
Electrons as waves:
- For light, energy of a photon, E = hn
Einstein also showed E = mc2
So mc2 = hn = hc / l, and therefore l = h / mc
- By analogy, de Broglie suggested for any particle moving with velocity v
l = h / mv (eq. 3.1)
For given v: if m is large, have
small l.
For given m: if v is large, have
small l.
- Electrons can be diffracted just like light! A Ni crystal will diffract a beam of electrons. The spacing between the Ni atoms is comparable to the wavelength of the electrons.
The de Broglie equation is confirmed.
- Electrons exhibit wave properties. Electron
waves Y("psi") in atoms and molecules called orbitals.
We must use a model for atoms and molecules that incorporates the wave properties of electrons.
- Atoms can be diffracted too!
To sum up:
- Light: behaves like particles and waves
- Electrons: behave like particles and waves.
More about electron "waves"
- Because of its wavelike character cannot say
precisely where an electron is when it is travelling along a path.
This is expressed in Heisenberg's Uncertainty Principle:
- The more precisely we know the position of
a particle the less we can say about the speed (and vice versa).
If we know the position of a particle of mass m
to within a range Dx then its momentum must be uncertain by at least an amount Dp
where
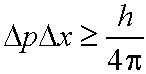 eq. (3.2)
eq. (3.2)
(h is Planck's constant)
Example: What is the minimum uncertainty in the
speed of an electron Dv in an H atom given the uncertainty in
its position, Dx, is the diameter of the atom (10-10 m)?
Method: Estimate Dv from Dp since p=mDv
From eq. (3.2)
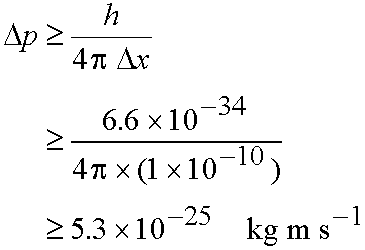
and

- If Dx is small, Dp must be very large!
If Dp is small, Dx must be very large!
- Pictures of electrons in precise orbits cannot
be valid because the electron would then have a definite position
and momentum at any instant. Need a completely different picture
incorporating wave properties!
- Electron waves (more correctly wavefunctions) Y ("psi") in atoms and molecules are called orbitals.
- The interpretation of electron wavefunctions (orbitals) is that we talk about the probabilities of an electron being at a particular place, e.g., being at a given
distance from a nucleus.
- If the probability of finding an electron at some point is high then the electron density is large at that point.
- How is the probability linked to the wavefunction Y? Basic idea is due
to Born. He suggested ("postulated") the probability of finding a particle in a small region of volume dV is
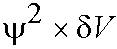
If Y2 is large at a particular point there is a high probability of finding the electron at that point.
- For each energy level there is an associated orbital, Y e.g., for the H atom have 1s, 2s, 2p etc.
- How do we find out the allowed energy levels
E and corresponding Y for atoms and molecules? We use a famous
equation suggested by Schrödinger.
Input: All the interactions involving the electrons and the nuclei (classical
electrostatics)
Output: The allowed E and corresponding Y.
EXAMPLES:
Quantum mechanical pictures of two systems:
(i) H atom
(ii) large conjugated organic molecules
HYDROGEN ATOM
- Experiment: Spectrum of atomic H consists of series of narrow lines - major
evidence for the quantization of energy.
- Each series looks like:
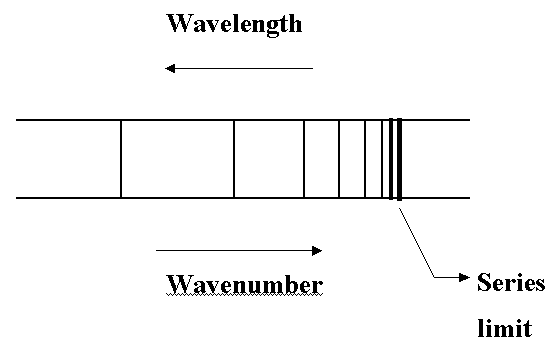
- Quantum theory shows allowed energy levels of the H atom are:
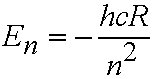 eq. (4.1)
eq. (4.1)
h is Planck's constant, c speed of light. R is the
Rydberg constant (109,678 cm-1).
n is the PRINCIPAL QUANTUM NUMBER. n can take integer values 1,2,3..........
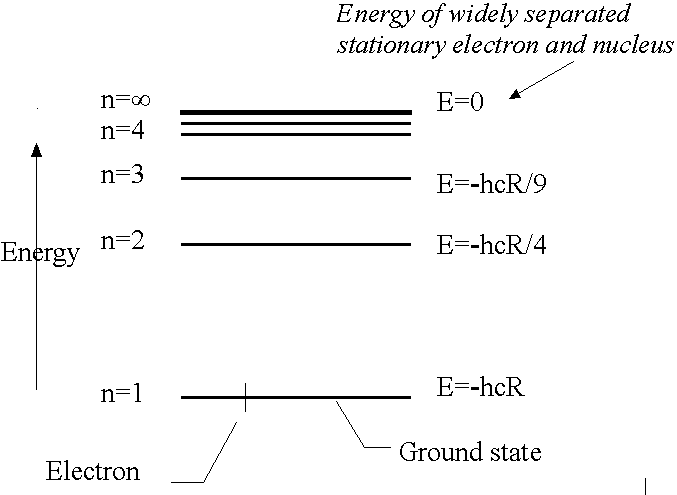
- Energy levels are widely separated at low values of n but they converge as n increases.
- Zero of energy (n=infinity) corresponds to the infinitely separated and stationary electron and nucleus, i.e., the ionised H atom. Relative to this all energies
described by eq. (4.1) are negative: the states it describes are the bound states of the atom.
- The lowest energy state is n=1, E1 = -hcR GROUND STATE
First excited state is n=2, E2=-hcR/4.
The ionisation energy is the minimum energy required to remove the electron from the H atom in its ground state (n=1). E1 = -hcR = -2.18x10-18 J
so the ionisation energy is +2.18x10-18J (1312 kJ mol-1)
- Explains the spectrum of the H atom quantitatively! Each line corresponds to a transition between two energy levels.
For transition from level with quantum number n1 to level with quantum number n2 (n2> n1)
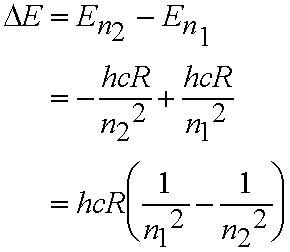
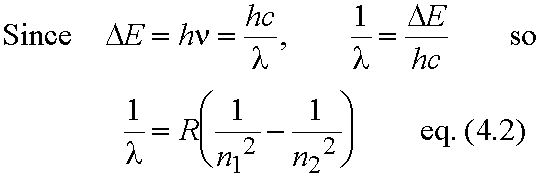
- All the lines in the spectrum fit this formula eq. (4.2).
Lyman series: n1=1 n2=2,3,4,5,6.....
Balmer series: n1=2 n2=3,4,5,6.....
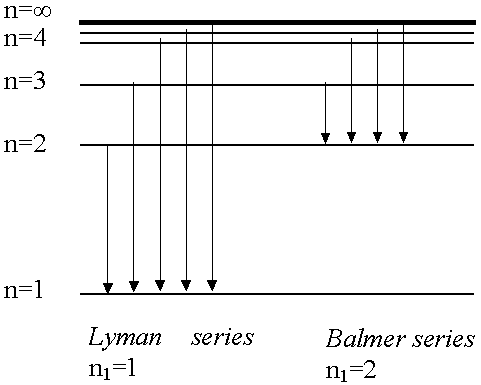
- Absorption spectrum of H atom only consists of one series
of lines (n1=1 to n2=2,3,4...) since all atoms at room temperature are in the ground state (n1=1). If pass electric discharge through H atoms, excite atoms to many excited states and in emission spectrum we see
several series of lines as electrons jump down to lower levels from higher levels.
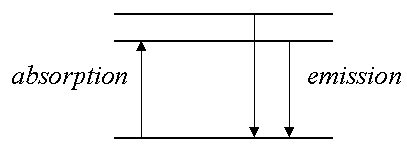
- Associated with each energy level is a wavefunction Y. For one-electron systems the Y are called orbitals. When an electron is described by one of these wavefunctions we say that it occupies that orbital.
e.g., the n=1 level corresponds to the 1s orbital.
the n=2 to the 2s, 2p orbitals.
the n=3 to the 3s, 3p, 3d orbitals.
In the H atom 2s, 2p orbitals are DEGENERATE (=have same energy), similarly 3s, 3p, 3d orbitals have same energy, i.e., energy depends ONLY on the principal quantum number n (eq.
(4.1)). ONLY true for one-electron systems!
- In many-electron atoms 2 electrons (with opposite
spin) can occupy any orbital. Similarly in molecules 2 electrons
can occupy any molecular orbital which can extend
over many atomic centres.
CONJUGATED ORGANIC COMPOUNDS
- "Particle-in-a-box" model for p-electrons
in molecules such as H2C=CH-CH=CH2.
- The p-electrons are confined to the molecule - assume the potential energy of the electrons is zero throughout the molecule.
- The key to explaining the energy levels of the electrons is their wave properties. The electrons are confined, and so the electron waves are "standing" waves.
- Compare waves on a guitar string which is fixed at both ends. Only certain wavelengths are possible for vibrations - the wavelengths of the allowed vibrations
must be such that a whole number of half-wavelengths are equal to the length of the box.
- Let the molecule (length L) lie along the x-axis between x=0 and x=L.
e.g.,
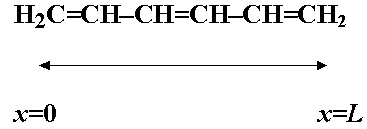
- So any electron wave/wavefunction Y must
be zero for x<=0 and x>=L. Zero probability
of finding electron outside box. Wavelengths l
can ONLY be
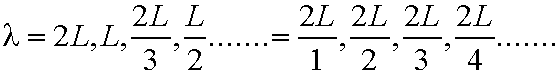
In general
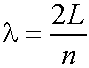 n=1,2,3,4 eq. (5.1)
n=1,2,3,4 eq. (5.1)
From De Broglie,
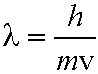 (eq. 3.1), and
(eq. 3.1), and
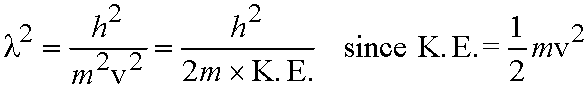
So substituting for l from eq. (5.1),
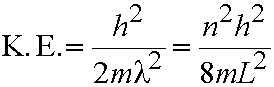
 n=1,2,3,4....eq.(5.2)
n=1,2,3,4....eq.(5.2)
where n is a quantum number.
- The corresponding wavefunctions Y are:
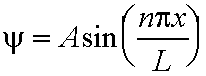 for 0 <=x <=L, n=1,2,3...eq.(5.3)
for 0 <=x <=L, n=1,2,3...eq.(5.3)
See handout.
- Energy quantized! So we have a set of allowed
energy levels and corresponding wavefunctions Y (orbitals).
- As n increases, the energy increases and the number of nodes in Y increases. A node is where passes through zero. Y for n=0 has zero nodes, Y for n=1 has 1 node (in the middle), Y for n=2 has 2 nodes. Probability of finding electron at a node is 0.
N.B. The edges of the box where Y=0 are not nodes - Y does not pass through zero at edges.
- The lowest possible energy is not zero, but is the energy for n=1 (E=h2/8mL2). This is the zero-point energy.
- EXAMPLE: Apply model to butadiene,
H2C=CH-CH=CH2
We have 4 p-electrons, which fill up the lowest 2 p-orbitals. Length of molecule is L.
n=1 and n=2 are the occupied p-orbitals. n=2 is the HOMO (highest occupied molecular orbital), n=3 is the
LUMO (lowest unoccupied molecular orbital).
- Lowest energy electronic transition is when an electron is excited from the HOMO to the LUMO (here n=2 to n=3). This transition occurs in the ultra-violet region
of the spectrum.
- In general consider transition between adjacent levels - from level with quantum number n to the level with n+1. Energy gap, DE,
given by:

- So DE decreases as L increases. As the
chain length increases, i.e., as go down series,
H2C=CH-CH=CH2
H2C=CH-CH=CH-CH=CH2
H2C=CH-CH=CH-CH=CH-CH=CH2 etc.
then HOMO-LUMO separation DE decreases.
- Since DE=hn then the frequency of light absorbed when this transition takes place decreases as L increases, and for large conjugated carbon chains this transition takes place in the visible region. Hence COLOUR. Basis of dye industry.
- The multiple choice questions "Basic ideas in physical science" are on the Web.



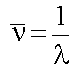 eq.(1.2)
eq.(1.2)![]() are m-1,
though usually quoted in cm-1.
are m-1,
though usually quoted in cm-1.![]() .
.

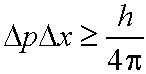 eq. (3.2)
eq. (3.2)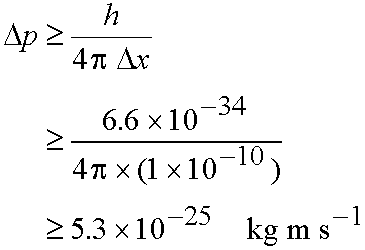

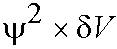

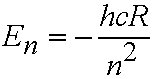 eq. (4.1)
eq. (4.1)
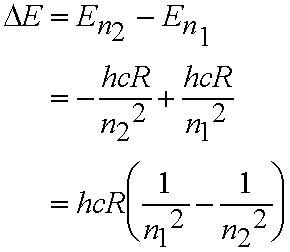
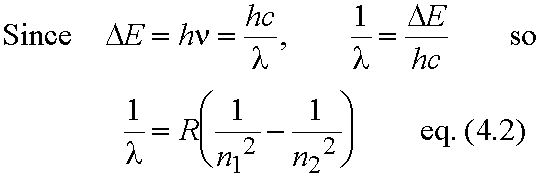


 n=1,2,3,4 eq. (5.1)
n=1,2,3,4 eq. (5.1) (eq. 3.1), and
(eq. 3.1), and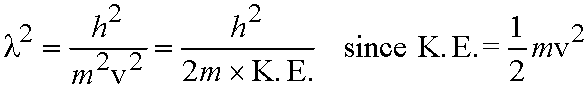
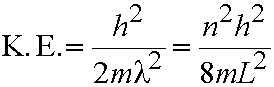
 n=1,2,3,4....eq.(5.2)
n=1,2,3,4....eq.(5.2)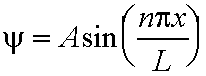 for 0 <=x <=L, n=1,2,3...eq.(5.3)
for 0 <=x <=L, n=1,2,3...eq.(5.3)