Chapter 4

Electrochemical theory for diamond electrodes

4.1. Introduction

Diamond has been suggested as a very attractive electrode material due to its remarkable properties (outlined in chapter 1). The electrochemistry of diamond resembles that of a metal. However diamond is a semiconductor. Standard theory cannot explain the electrochemical behaviour of boron doped diamond.

After a basic review of metal electrochemistry, a new theory to explain the electrochemical behaviour of boron doped diamond is introduced that is based on surface state mediated electron transfer. The new theory is used to predict the influence of changing doping density on the electrochemistry.

4.2. Metal Electrochemistry

Marcus-Gerischer theory¹ as applied to basic electrochemistry at a metal electrode² is introduced in this section. The essential idea is that the electron transfer occurs between occupied and unoccupied states that are equal in energy ³.

The theory relates the overpotential, h, to the total current density, j, at the metal-solution interface. This total current density is defined as the sum of the anodic current density, j_a, and the cathodic density current, j_c. Cathodic current is considered negative by convention.

j = j_a + j_c [equation 4.1]

Anodic density current flows when the oxidation process occurs at the electrode surface

R → O + e^-

(e.g. : Fe²⁺_(aq) → Fe³⁺_(aq) + e^-)

Cathodic density current flows when the reduction process occurs at the electrode surface

O + e^-→ R

(e.g. : Fe³⁺_(aq) + e^-→ Fe²⁺_(aq))

To reduce difficulties in the mathematical development the Frank-Condon approximation is applied to the electron transfer process, i.e., the nuclei, being much heavier relative to electrons, move slowly compared to electrons and can be considered as stationary during the electron transfer process ⁴. The electrons are transferred to energy levels at or near the Fermi level in the metal. In an electrochemical experiment a modification in the applied potential results in charging of the metal, i.e., the metal surface potential is modified. Therefore the Fermi level changes its position in the metal when the applied potential is modified. However for a metal no modification occurs in the occupation of the states about the Fermi level. Hence, current densities are simply proportional to the overlap integral of the Fermi junction in the metal and the density of the states function for the solution species:

j_a µ (overlap of E_F and E_R)

j_c µ - (overlap of E_F and E_O)

When the equilibrium potential is reached, the overlap integrals are equal. Therefore the values for j_a and j_c are equal in magnitude with opposite sign. As a result the net current density is zero. (See figure 4.1, focus on the plot on the left side of the figure).

When the equilibrium is perturbed and a positive overpotential (considering overportential as the deviation of the potential from the equilibrium value ⁵) applied, the overlap integral for the reduced electrochemical species is much bigger than for the oxidised species. An anodic current flows and net oxidation occurs. (See figure 4.1, focus on the plot on the upper right side of the figure).

When a negative overpotential is applied the overlap integral for the oxidised electrochemical species is much bigger that the same for the reduced species. The net current density is negative. A cathodic current flows and reduction of the electrochemical species occurs. (See figure 4.1, focus on the plot on the lower right side of the figure).

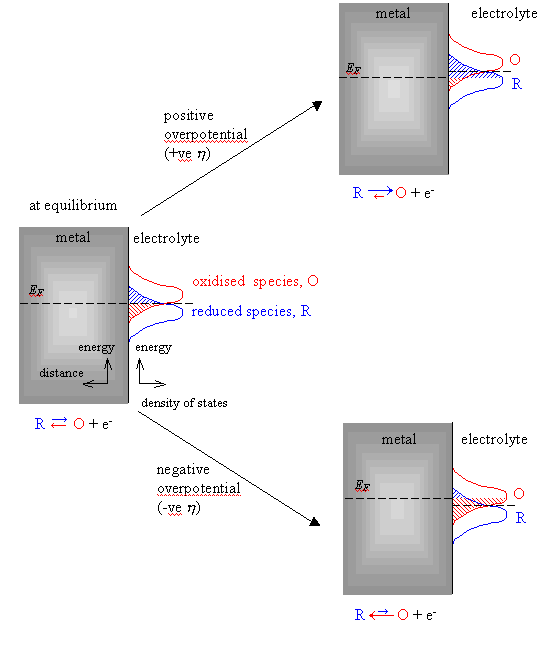
Figure 4.1. Schematic distribution functions on the rate of electron transfer for a metal-solution interface.

Figure 4.2 shows a sketch of current density versus overpotential for electron transfer at a metal/ solution interface. Current density and overpotential are related by the Butler-Volmer equation.

[equation 4.2]

where j: current density R: gas constant

j_o: exchanged current density T: temperature

a: transfer coefficient h: overpotential

F: Faraday constant

The plot shown in figure 4.2 assumes a = 0.5.

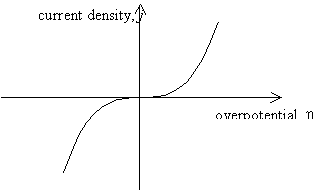
Figure 4.2. Current density – overpotential relationship for a=0.5

4.3. Ideal p-type Semiconductor Electrochemistry

In a p-type semiconductor the majority change carriers are positive holes in the valence band.

Anodic reaction

R + h⁺_(VB) → O

(e.g.: Fe²⁺_(aq) + h⁺_(VB) → Fe³⁺_(aq))

Cathodic reaction

O → R + h⁺_(VB)

(e.g.: Fe³⁺_(aq) → Fe²⁺_(aq) + h⁺_(VB))

Unlike metals no states are available at the Fermi level and charge transfer only occurs at the surface energy of the valence band, E_VB,S. The anodic current that flows at the semiconductor electrode is dependent on the surface concentration of majority change carriers and the overlap integral of E_VB,S and E_R:

j_a µ (overlap of E_VB,S and E_R) ´ ( [h⁺]_surface ).

However, the cathodic current is basically constant because the electron disposability remains approximately constant.

j_c µ -(overlap of E_VB,S and E_O).

When a positive overpotential is applied (see figure 4.4., focus on the plot of the right upper side on the figure), the thermodynamics indicates that the system is no longer at equilibrium and oxidation will occur. However, to determine current densities the rates of the reduction must be considered and not the thermodynamics. If it is assumed that the overpotential is dropped across the space charge layer, i.e. only band bending is modified and there is no change in the overlap terms at the valence band edge. However, the concentration of holes at the surface is increased.

Therefore

j_c = j_c,0 and j_a > j_a,0

where j_c,0 is the exchange cathodic density current and j_a,0 is the exchange anodic density current. The net positive current flux is positive. When a high positive overpotential is applied the concentration of the holes at the surface increases steeply (an exponential relationship between the surface concentration and the overpotential applies) and j_a >> j_a,,0.

When a negative overpotential is applied (see figure 4.4, focus on the plot on the right middle side of the figure), the thermodynamics indicates that the system is no longer at equilibrium and reduction will occur. Focusing on the current densities and therefore on the rates of the reduction and oxidation process rather that the thermodynamics, there is no change in the overlap terms at the valence band edge but concentration of holes at the surface is decreased. Therefore

j_c = j_c,0 and j_a < j_a,0

that produces a net negative current flux. When a high negative overpotential is applied the concentration of the holes at the surface approaches zero and a limiting current density of j_c,0 (a negative current) is obtained.

When a very negative overpotential is applied (see figure 4.4, focus on the plot on the left bottom side of the figure), the band bending at the surface may be sufficiently high that the Fermi level lies within conduction band. There is a finite probability of finding an electron in the conduction band at the surface. Reduction can then occur by the following reaction

O + e^-_(CB)→ R

(e.g.: Fe³⁺_(aq) + e^-→ Fe²⁺_(aq))

The cathodic current is then potential dependent. This phenomenon is known as inversion.

In the absence of inversion when an increasing positive overpotential is applied, the total density current rises very quickly. However if a decreasing negative overpotential is applied, the current density drops to a constant value with the magnitude of the equilibrium cathodic current density, j_c,0, as shown in figure 4.3.

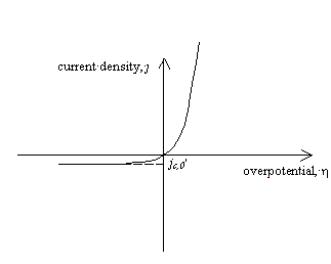
Figure 4.3. Current density as function of overpotential for a semiconductor

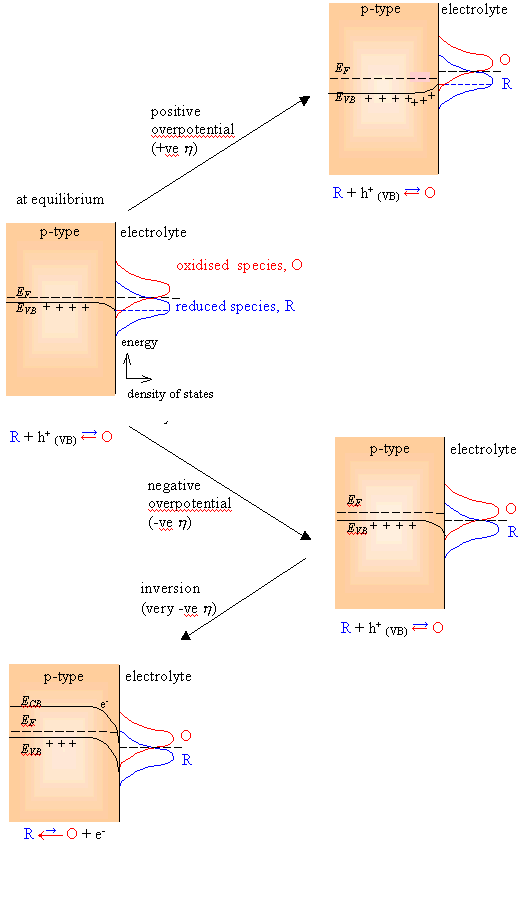
Figure 4.4. Schematic distribution functions on the rate of electron transfer for a semiconductor-solution interface

4.4. Highly doped semiconductors

When a semiconductor is highly doped the Fermi level of the semiconductor may lie within the valence band (VB) and the space charge region is very small. Electrons are able to tunnel from the bulk of the valence band directly to the electrolyte. When this occurs the semiconductor is said to be degenerately doped.

Considering the Frank-Condon approximation to charge transfer at a degenerately doped electrode indicates that electrons are transferred at or to energy levels close to the Fermi level.

As the concentration of charge carriers available for exchange is constant (from the bulk) at a degenerately doped electrode the current densities are:

j_a µ (overlap of E_F and E_R)

j_c µ - (overlap of E_F and E_O)

When the equilibrium potential is reached the overlap integrals are identical. Hence j_a ad j_c are equal and the net current density is zero (by definition j_c is negative).

When a positive overpotential is applied

(overlap of E_F and E_R) > (overlap of E_F and E_O)

then

j_a < j_c Þ j > 0

When a negative overpotential is applied

(overlap of E_F and E_R) < (overlap of E_F and E_O)

then

j_a > j_c Þ j < 0

Therefore these electrodes show metal behaviour. This behaviour is shown in the schematic for figure 4.5.

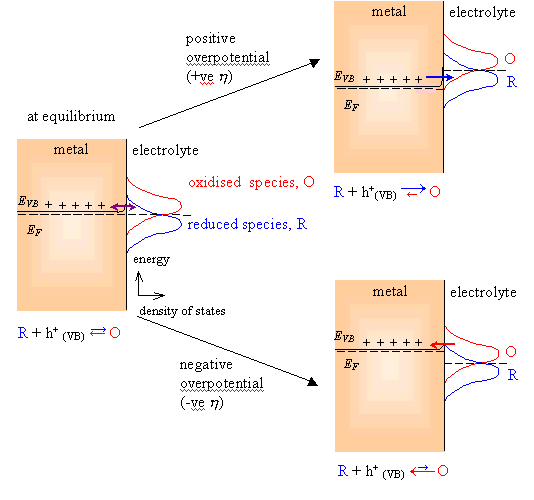
Figure 4.5. Schematic distribution functions on the rate of electron transfer for a heavily doped semiconductor-solution interface.

Current voltage curves therefore resemble those at a metal, i.e., reduction and oxidation are found in the plot, see figure 4.6.

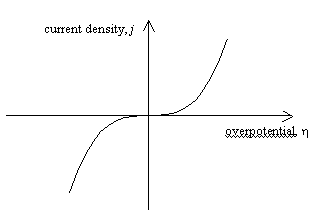
Figure 4.6. Current density as a function of overpotential for a heavily doped semiconductor.

4.4.1. Electrochemistry at Boron Doped Diamond Electrode

Many studies have been done that report metal behaviour for boron doped diamond electrodes ^6-41.

Two possible explanations for metal behaviour on boron doped diamond are:

· The samples are degenerately doped.

· Contamination of the samples provides a conduction path through the films. Possible sources of contamination are tantalum (Ta) from the filaments of the hot filament CVD chamber and graphite (C) formed during the diamond growth.

These reasons can be discounted as boron doped diamond displays:

· A Mott-Schottky regime ^{10, 42}.

· Two time constants are measured in impedance experiments on boron doped diamond ¹⁰.

For an alternative explanation of the metallic behaviour on highly doped diamond, the position of the conduction band minimum, the valence band maximum, the energy of the surface states and the Fermi level relative to the energy levels of the redox species in solution need to be considered.

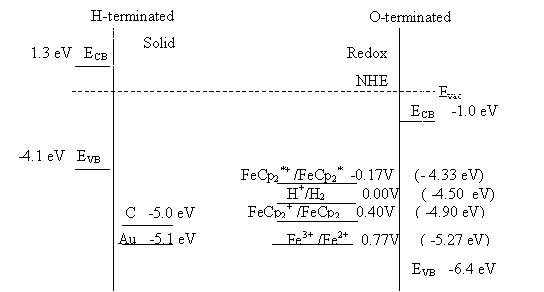
Figure 4.7. Schematic energy level diagram showing the band edges of the semiconductor and the energy levels of redox species ⁴³. Redox potentials from CRC book ⁴⁴.

For boron doped diamond the surface termination needs to be considered:

· Hydrogen terminated diamond samples

· Oxygen terminated diamond samples

4.4.1.1. Hydrogen surface termination on highly doped diamond

For hydrogen terminated diamond samples, the valence band maximum lies at higher energy than the proton redox couple ¹⁰. In aqueous solution, holes will accumulate at the surface.

A surface charge on the semiconductor and the potential across the Helmholtz layer will result in the material behaving in a metallic way. Figure 4.8 is a schematic of the contact process between diamond and a standard hydrogen reaction as an example.

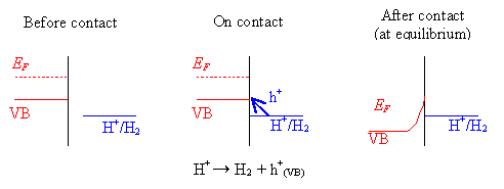
Figure 4.8. Reaction at a hydrogen terminated surface

4.4.1.2. Oxygen terminated surface on highly doped diamond

The redox levels in solution lie between the CB and VB. For a perfect single crystal diamond classic semiconductor behaviour would be expected ⁴² . However, CVD polycrystalline doped diamond contains a high density of grain boundaries. Grain boundaries are known to provide trapping states ^{45, 46}. The grain boundaries are graphitic in nature suggesting they will lead to a density of surfaces states at an energy of approximately –5.0 eV ^{2, 5}(see figure 4.7). This energy level is comparable to the energy levels of the redox couples in solution. To fully investigate the role of the surface states in the mechanism requires a theory to describe in detail the mechanism of surface state mediated charge transfer must be developed.

Figure 4.9 shows a schematic of the contact process for an oxygen terminated diamond surface, which includes the surfaces states. The diagram explains a determinate situation when the potential drop across the Helmholtz layer is constant.

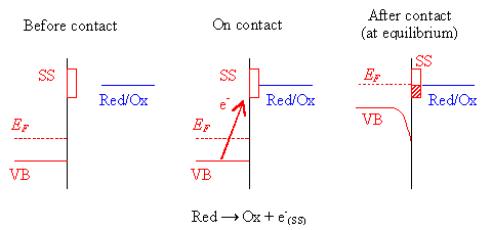
Figure 4.9. Contact process for an oxygen terminated diamond surface (SS: surface state)

4.5. Surface State Mediated Electron Transfer

Electron transfer via surface states is often mentioned to explain some anomalies in semiconductor electrochemistry ⁵.

Figure 4.10. Electron tranfer via surface states

In the literature little information is available about the theory of charge transfer mediated by surfaces states. Only Chazaviel et al. ⁴⁷ and Vanmaekelbergh et al. ^{48, 49} consider the possibility of a charge transfer mediated by surface states in an n-type semiconductor.

In this section the Chazaviel model, which uses the Marcus-Gerischer theory, discussed above, will be developed for a p-type semiconductor. The model assumes that the only pathway for electron transfer is a two step process which involves the transfer between the redox system and the semiconductor surface and the transfer between the semiconductor surface and the semiconductor bulk. Another assumption is that the distribution function for the surface states obeys Fermi statistics, even under nonequilibrium conditions; in other words, the electrons in the surface states are thermalized to lattice temperature, and only the position of their Fermi level can be changed.

4.5.1. Contributions to the Applied Potential

The variation that the applied potential experiences across a semiconductor electrode-solution interface, dV, has two components: the potential difference across the space charge region in the solid, dV_SC, and the potential difference across the Helmholtz layer in the solution, dV_H.

dV = dV_SC + dV_H [equation 4.3]

Here the importance of an ohmic contact is apparent, it is required to avoid a potential drop across the contact.

4.5.2 Contribution of the Helmholtz layer and the space charge region

The capacitance of the Helmholtz layer, C_H, is assumed to be much bigger than that of the space charge region, C_SC. This fact implies that modifications in the potential drop across the Helmholtz layer, dV_H, are only due to changes in the surface charge dQ.

C_SC << C_H

[equation 4.4]

4.5.3. Electrical charge at the surface of semiconductor electrode

The change in the surface charge is a function of the modification in the Fermi level energy at the surface, E₀, and the density of the states at the surface, per unit of energy r_SS.

[equation 4.5]

Reordering the above equation:

[equation 4.6]

Substituting equation 4.6 in equation 4.4 yield:

[equation 4.7]

Assuming that the distribution of the surface states is uniform equation 4.7 is transformed to:

[equation 4.8]

Regrouping terms of the equation:

[equation 4.9]

4.5.4. The Butler-Volmer Equation

Electron transfer across the Helmholtz layer is governed by the Butler-Volmer equation ³.

In a non-equilibrium situation, there is a difference in the energy between electrons in the surface states and the redox couple. The Butler-Volmer equation relates the current density to the potential drop across the Helmholtz layer.

Assuming efficient mass transport:

[equation 4.10]

If a=0.5

[equation 4.11]

4.5.5. Schottky Diode.

The bulk semiconductor-surface state junction may be modelled as a Schottky diode ⁵⁰.

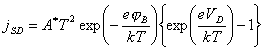
[equation 4.12]

Where j_SD= current across the space charge layer

V_D= the potential drop between the space

charge and the bulk semiconductor (the forward bias)

j_B = barrier height

Figure 4.11 shows the relationship between forward bias and conventional electrochemical current for n-type and p-type semiconductors.

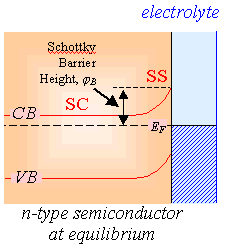
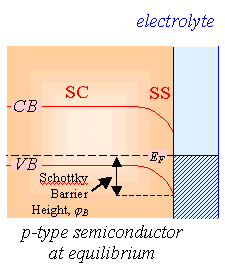
Figure 4.11. Forward bias and conventional electrochemical current. V_D is the potential drop between the semiconductor surface (SS) and the semiconductor bulk (SC).

4.5.6. Model

Figure 4.12 below reflects the influence of applying a positive potential to a semiconductor interface at which there is a high density of surface states.

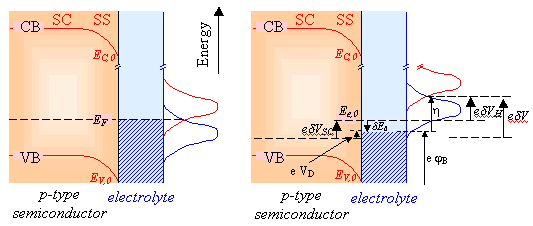
Figure 4.12. Schematic energetic diagram at positive potential

Expressions relating the potential drop across each component can be obtained

[equation 4.15]

[equation 4.16]

[equation 4.17]

Substituting the expression for the overpotential (equation 4.15) into

[equation 4.18]

yields:

[equation 4.19]

When the semiconductor-surface state junction is considered as a Schottky-diode the current across the space charge region is:

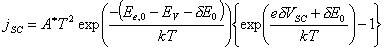
[equation 4.20]

Hence, the space charge current across, j_SC,0, at equilibrium is:

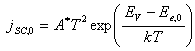
[equation 4.21]

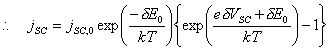
[equation 4.22]

4.5.7. Steady State Current

When the steady state is reached the net current density, j, is equal to the current density in the Helmholtz layer and current density in the space charge region.

j_SC = j_H = j [equation 4.23]

Substituting equation 4.9 into equation 4.19 gives:

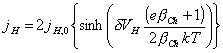[equation 4.24]

Rewriting the above equation, the expression for the applied potential in the Helmholtz layer gives:

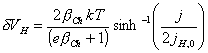[equation 4.25]

Substituting into equation 4.22:

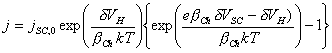[equation 4.26]

Expanding the equation:

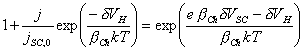[equation 4.27]

Applying the logarithmic fuction:

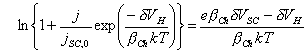[equation 4.28]

Reorganizing the equation:

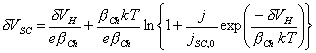[equation 4.29]

Simplyfying the above equation:

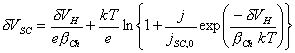[equation 4.30]

the applied potential in the space charge region is obtained.

Substituing equation 4.3 into the equation 4.30 gives:

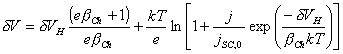
[equation 4.31]

for the net applied potential.

Applying equation 4.25 to the above equation:

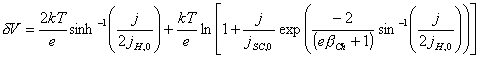
[equation 4.32]

Considering that

[equation 4.33]

then

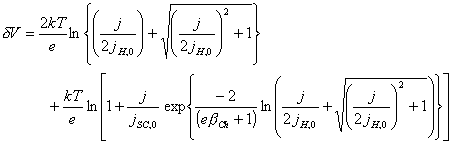
[equation 4.34]

Reorganizing the equation

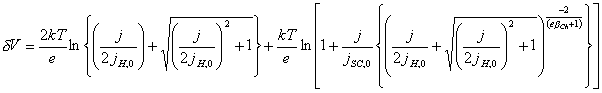
[equation 4.35]

the net applied potential is expressed in terms of the current density.

4.6. Developing the model

The model disscused in the last section was a development of the theory of Chazalviel ⁴⁷. It is based a the assumption that C_H >> C_SC (see section 4.4.2.). A new model is required when this supposition is not valid. The system must be modelled by accounting for the potential drop across both the space charge region and the Helmholtz layer.

The space charge region and the Helmholtz layer can be modelled as connected in series. Each region performs as a resistor in parallel with a capacitor.

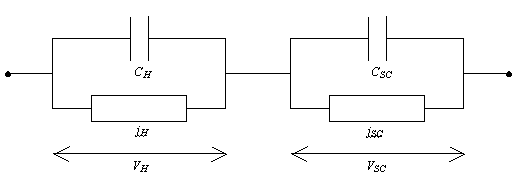
Figure 4.13. Equivalent circuit for surface mediated transfer with significant potential drop across the Helmholtz layer.

To describe the new model it is necessary to calculate the relationship between current density and the applied potential. Considering the above equivalent circuit and applying Kirchoff’s laws:

[equation 4.36]

and

[equation 4.37]

Using equation 4.37 to eliminate dV_SC from equation 4.36 yields:

[equation 4.38]

where Q_SS is the charge on the surface states.

If the density of surface states per unit energy (eV) is r_SS(E₀)

[equation 4.39]

Hence:

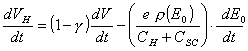[equation 4.40]

or [equation 4.41]

where 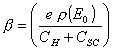[equation 4.42]

If the capacitances, C_H and C_SC, and the density of states, r(E₀), are potential independent the equations can be rewritten as:

[equation 4.43]

and

[equation 4.44]

Substituting equation 4.15 into equation 4.11 (the Butler-Volmer equation for a=0.5)

[equation 4.19]

Substituting 4.43 into 4.19 yields

[equation 4.45]

Regrouping terms yields

[equation 4.46]

Reordering the above equation:

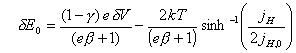[equation 4.47]

The current across the space charge region, j_SC can be fitted as a Schottky diode (substitute equation 4.44) into the equation 4.22:

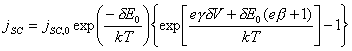[equation 4.48]

Substituting equation 4.47 into 4.48 yields:

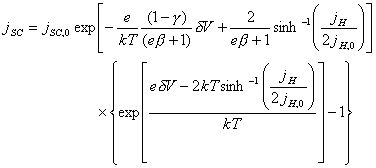
[equation 4.49]

When the steady state is reached, the stored charge is constant and the current through the Helmholtz layer is equal that the space charge region

j = j_H = j_SC [equation 4.50]

Therefore, the equation 4.50 can be rewritten:

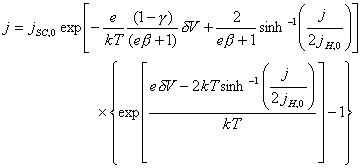
[equation 4.51]

Equation 4.51 is an expression for the current density, j, that modifies with the applied overpotential, dV. The rest of the terms are constant. No analytical solution to the equation can be obtained and numerical methods are necessary required then.

Mathcad 8 Profesional (MathSoft, Inc.) was operated to find numerical solutions. The software could automatically select an appropriate algorithm to solve a given equation. The solutions found by numerical means were not necessarily unique.

It is usual in semiconductor electrochemistry to suppose that the capacitance of the Helmholtz layer to be much bigger than that of the space charge region (C_H>>C_SC). If that is the case, then g tends to unity (g®1) and the equation can be solved analytically.

When g=1, then equation 4.51 simplifies to equation 4.32:

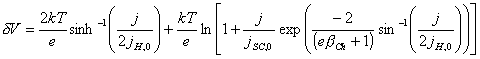
[equation 4.32]

i.e. the general model obtains the particular case of the Chazaviel model, when g®1.

4.6.1. The case when ½j_H,0½>>½j½

For the case when ½j_H,0½>>½j½, several terms in equation 4.51 become negligible. This leads to much simpler relationship shows in the equation 4.52.

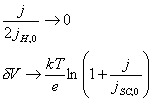[equation 4.52]

Figure 4.14 shows a Mathcad plot for the equation 4.51 when ½j_H,0½>>½j½. The behaviour is independent of b and is typical of a p-type semiconductor.

Figure 4.14. Equation 4.51 plotted for |j_H,0|>>|j|.

From the figure 4.14 it can be deduced that when ½j_H,0½>>½j½, ideal semiconductor behaviour is expected for boron doped diamond. Such behaviour is not reached in the experimental conditions. Factors like the diffusion of the electrolyte (or redox couple), possible chemical reaction on the surface, etc avoid an ideal semiconducting behaviour. Thefore the figure 4.14 represents a boundary situation.

4.6.2. The case when ½j½>>½j_H,0½

When ½j½>>½j_H,0½,

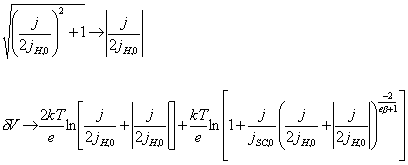[equation 4.53]

For positive j:

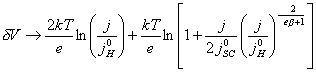[equation 4.54]

For negative j:

[equation 4.55]

When negative potentials are applied, the current density is independent of the applied potential.

Figures 4.15 show Mathcad plot of equation 4.51 for the case when ½j½>>½j_H,0½. The behaviour is independent of b and is typical of a p-type semiconductor.

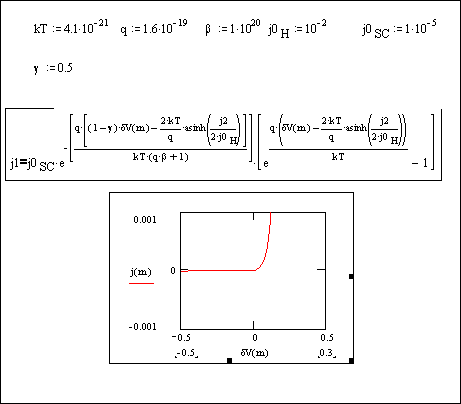
Figure 4.15. Equation 4.51 plotted for |j_H,0|<<|j|.

Figures 4.15 suggests an ideal semiconductor behaviour for boron doped diamond when ½j½>>½j_H,0½. Diffussion effects, possible chemical reactions on the electrode surface, etc. can contribute in the deviation of the results obtained in experimental conditions from the situation expressed in the figure 4.15.

4.6.3. The case when ½j_SC,0½>>½j½ and j» j_H,0

For the case when ½j_SC,0½>>½j½ and j» j_H,0, equation 4.51 simplifies to equation

4.56.

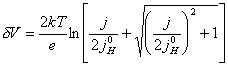[equation 4.56]

Figure 4.16 shows a Mathcad plot equation 4.51 for the case when ½j_SC,0½>>½j½. The behaviour is independent of b and is classic metal behaviour.

Figure 4.16. Equation 4.51 plotted for |j_SC,0|>>|j|.

Figure 4.16 shows the standard metal behaviour for boron doped diamond. In these conditions surface states promote the electron transfer in such as way that metal behaviour is obtained.

4.6.4. Considering doping levels

When high doping levels are reached, j_SC,0 values are high. Metal behaviour is observed. Reducing the doping level, implies that j_SC,0 becomes more important and semiconductor behaviour is observed.

Figures 4.17 and 4.18 show Mathcad plots of equation 4.51 for different values of b and the rest of parameters equal.

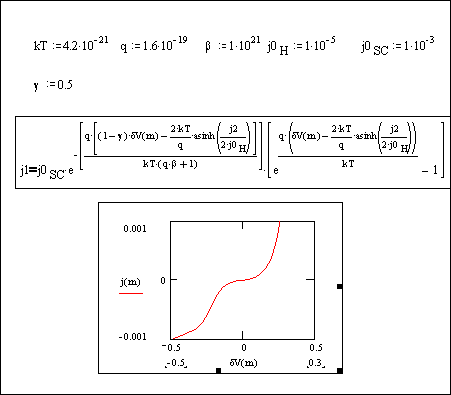
Figure 4.17. Equation 4.51 plotted for |j_SC,0|>|j| and b=1´10²¹.

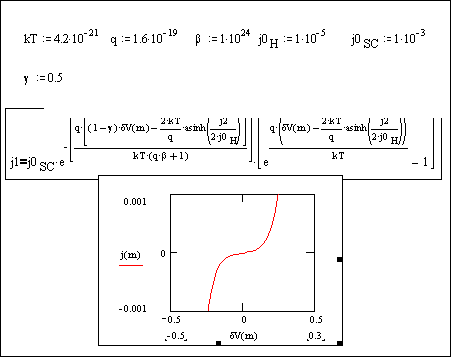
Figure 4.18. Equation 4.51 plotted for |j_SC,0|>|j| and b=1´10²⁴.

Figure 4.17 shows a intermediate situation between metal behaviour and ideal behaviour for boron doped diamond. It behaves as semiconductor (electron transfer is not as easy as in a metal) but it shows a maximum for a region of the curve, typical of a metal behaviour. Figure 4.17 shows the typical behaviour in experimental conditions for a low doped diamond sample (see chapter 5).

Figure 4.18 shows metal behaviour. When the doping level is increased boron doped diamond behaves as a metal.

Summarising at this point, semiconductor behaviour will be observed for boron doped diamond if the total current density values are different enough from the values of Helmholtz current density values. In case that the total current density values are similar to the Helmholtz ones space charge current density plays an important role. When the magnitude of the space charge current density is much bigger than the one for the total current density, just only in this case, metal behaviour will be observed. Otherwise semiconductor behaviour remains.

4.7. AC Impedance

The surface state model can be extended to consider small amplitude modulations (symbolised by overtilde embellishments). To facilitate the mathematical development is considered that C_H>>C_SC, in other words that g»1

[equation 4.57]

Applying Kirchoff’s law:

[equation 4.58]

[equation 4.59]

Using the general equation for the current density across Helmholtz layer

[equation 4.19]

using equation above becomes

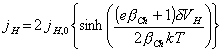[equation 4.60]

and applying small perturbations yields:

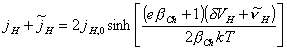[equation 4.61]

Expanding the above equation using

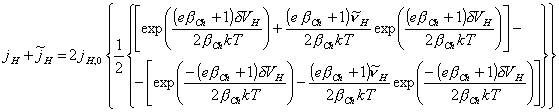
[equation 4.62]

As

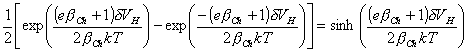
[equation 4.63]

and

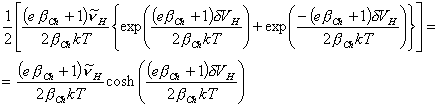
[equation 4.64]

The equation 4.62 is simplified to:

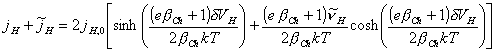[equation 4.65]

A further simplification can be done if

[equation 4.19]

leaving the equation 4.65 as:

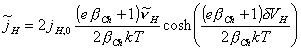[equation 4.66]

Rewriting the above equation as

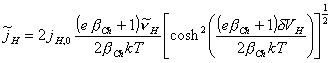[equation 4.67]

and considering

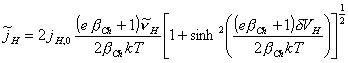[equation 4.68]

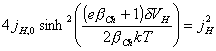[equation 4.69]

then the equation 4.68 yields:

[equation 4.70]

If the equation 4.70 becomes:

[equation 4.71]

The current density of the space charge layer using Chazaviel model for a p-type semiconductor is expressed

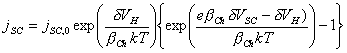[equation 4.72]

substituting equation 4.3 into the above equation yields

[equation 4.73]

Applying small perturbations yields

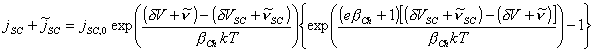
[equation 4.74]

Expanding the above equation

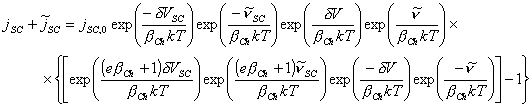
[equation 4.75]

Substituting in the small perturbation terms for exp(x) »1 + x and exp(y) »1 + y

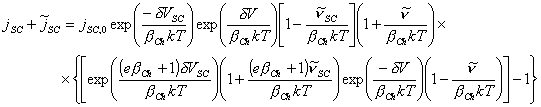
[equation 4.76]

Considering that x ´ y ® 0 the above equation yields:

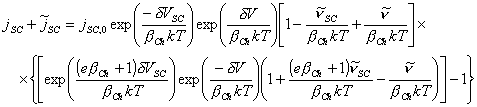
[equation 4.77]

Regrouping terms using equation 4.73 yields

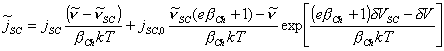
[equation 4.78]

For steady DC current, j=j_SC

and then equation 4.78 becomes:

[equation 4.79]

For a particular potential, j, b_Ch, j_H,0 and dV_SC remain constant. dV, dV_SC and j can be determined from steady-state measurements.

Equations 4.57,4.58,4.59,4.71, and 4.77 can be combined to lead to an expression which eliminates and .

Substituting the equation 4.71 into the equation 4.58 yields:

[equation 4.80]

and substituting the equation 4.79 into the equation 4.59 gives:

[equation 4.81]

Substituting the equation 4.57 into the equation 4.80

[equation 4.82]

Rewriting the above equation

[equation 4.83]

Substituting the equation 4.83 into the equation 4.81 gives:

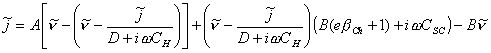
[equation 4.84]

Expanding the above equation:

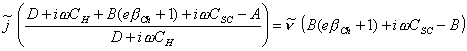
[equation 4.85]

[equation 4.86]

Therefore impedance is

[equation 4.87]

Considering the case when j=0 (at open circuit potential conditions), the expression in the equation 4.87 simplifies to:

[equation 4.88]

If eb_Ch>>1 (metal behaviour for highly boron doped diamond electrode) equation 4.88 becomes

[equation 4.89]

This expression for Z forms two semicircles when plotted in the complex plane. The first semicircle has a radius of 1/Beb_Ch with a maximum, w_max, of Beb_Ch /C_SC. The second semicircle has a radius of 1/D and a maximum, w_max, of D/C_H. This theory fits the experimental results found for several research groups^{10, 42, 51-53}.

When the conditions are not at open circuit potential, the behaviour is slightly more complicated and it is necessary to find values of j, dV and dV_SC from DC experiments.

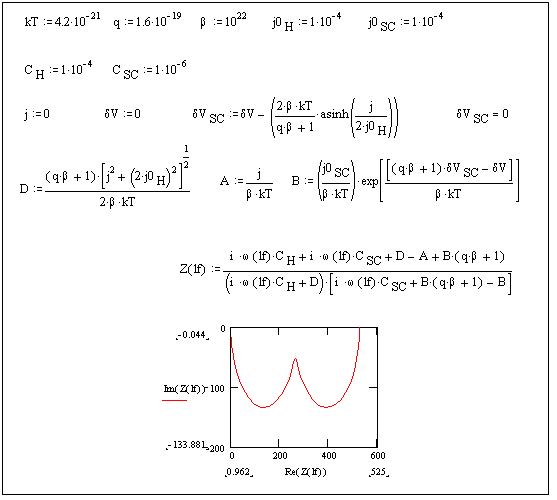
Figure 4.19. Impedance plot for open circuit potential conditions

Figure 4.19 shows two semicircles at open circuit potential conditions. This behaviour has been reported frequently for highly boron doped diamond electrodes ^10,
42.

In the effort to characterise properly the semiconducting behaviour of boron doped diamond the semicircle generated for the capacitance of the space charge layer (in the impedance plot) requires to be studied in detail. For this purpose the Mott Schottky equation (see chapter 5) relates the space charge capacitance per unit area and the potential of the surface with respect to the bulk semiconductor. In chapter 5 Mott Schottky plots are used to characterise the semiconducting properties of moderately boron doped polycrystalline diamond.

4.8. Summary

The standard theories for metal or semiconductor electrochemistry are outlined. The models do not agree with the electrochemistry of boron doped polycrystalline diamond films, reported in the literature.

The mechanism of charge transfer must be considered. The presence of a surface explains the difference in behaviour between hydrogen and oxygen terminated diamond films.

A relationship between the current density and applied potential has been derived. This agrees with the experimental results of these research groups ^{25-31,
33, 36, 37, 39-41, 54-65}, which show metallic behaviour. The theory suggests that at low doping levels semiconductor behaviour may be observed.

The surface state model was applied to the AC impedance studies and an expression was deduced that predicts the two time constants that have been observed for several groups.

The results from the AC impedance have been linked to the Mott Shottky equation to investigate the capacitance associated with the space charge layer that defines the semiconducting properties for boron doped diamond.

4.9. References

¹R. A. Marcus, J. Chem. Phys., 1965, 43, 679.

²S. R. Morrison, 'Electrochemistry at Semiconductor and Oxidized Metal Electrodes', Plenum Press, 1980.

³A. C. Fischer, 'Electrode Dynamics', Oxford University Press, 1996.

⁴P. Atkins, 'Physical Chemistry', Oxford University Press, 1994.

⁵A. J. Bard and L. R. Faulkner, 'Electrochemical Methods Fundamentals and Applications', 2001.

⁶F. J. Del Campo, C. H. Goeting, D. Morris, J. S. Foord, A. Neudeck, R. G. Compton, and F. Marken, Electrochem. Solid State Lett., 2000, 3, 224.

⁷S. Ferro, A. De Battisti, I. Duo, C. Comninellis, W. Haenni, and A. Perret, J. Electrochem. Soc., 2000, 147, 2614.

⁸D. Gandini, E. Mahe, P. A. Michaud, W. Haenni, A. Perret, and C. Comninellis, J. Appl. Electrochem., 2000, 30, 1345.

⁹C. H. Goeting, F. Marken, A. Gutierrez-Sosa, R. G. Compton, and J. S. Foord, Diam. Relat. Mater., 2000, 9, 390.

¹⁰M. N. Latto, D. J. Riley, and P. W. May, Diam. Relat. Mater., 2000, 9, 1181.

¹¹P. A. Michaud, E. Mahe, W. Haenni, A. Perret, and C. Comninellis, Electrochem. Solid State Lett., 2000, 3, 77.

¹²H. Notsu, I. Yagi, T. Tatsuma, D. A. Tryk, and A. Fujishima, J. Electroanal. Chem., 2000, 492, 31.

¹³Y. V. Pleskov, V. M. Mazin, Y. E. Evstefeeva, V. P. Varnin, I. G. Teremetskaya, and V. A. Laptev, Electrochem. Solid State Lett., 2000, 3, 141.

¹⁴T. N. Rao and A. Fujishima, Diam. Relat. Mater., 2000, 9, 384.

¹⁵T. N. Rao, B. V. Sarada, D. A. Tryk, and A. Fujishima, J. Electroanal. Chem., 2000, 491, 175.

¹⁶B. V. Sarada, T. N. Rao, D. A. Tryk, and A. Fujishima, Anal. Chem., 2000, 72, 1632.

¹⁷A. J. Saterlay, S. J. Wilkins, C. H. Goeting, J. S. Foord, R. G. Compton, and F. Marken, J. Solid State Electrochem., 2000, 4, 383.

¹⁸O. Chailapakul, P. Aksharanandana, T. Frelink, Y. Einaga, and A. Fujishima, Sensors and Actuators B-Chemical, 2001, 80, 193.

¹⁹J. S. Foord, K. B. Holt, R. G. Compton, F. Marken, and D. H. Kim, Diam. Relat. Mater., 2001, 10, 662.

²⁰A. Fujishima and T. N. Rao, Diam. Relat. Mater., 2001, 10, 1799.

²¹P. L. Hagans, P. M. Natishan, B. R. Stoner, and W. E. O'Grady, J. Electrochem. Soc., 2001, 148, E298.

²²K. B. Holt, J. Del Campo, J. S. Foord, R. G. Compton, and F. Marken, J. Electroanal. Chem., 2001, 513, 94.

²³F. Marken, Y. C. Tsai, A. J. Saterlay, B. A. Coles, D. Tibbetts, K. Holt, C. H. Goeting, J. S. Foord, and R. G. Compton, J. Solid State Electrochem., 2001, 5, 313.

²⁴F. Marken, R. G. Compton, C. H. Goeting, J. S. Foord, S. D. Bull, and S. G. Davies, J. Solid State Electrochem., 2001, 5, 88.

²⁵H. Notsu, T. Fukazawa, T. Tatsuma, D. A. Tryk, and A. Fujishima, Electrochem. Solid State Lett., 2001, 4, H1.

²⁶M. Panizza, P. A. Michaud, G. Cerisola, and C. Comninellis, J. Electroanal. Chem., 2001, 507, 206.

²⁷M. Panizza, P. A. Michaud, G. Cerisola, and C. Comninellis, Electrochem. Commun., 2001, 3, 336.

²⁸A. J. Saterlay, S. J. Wilkins, K. B. Holt, J. S. Foord, R. G. Compton, and F. Marken, J. Electrochem. Soc., 2001, 148, E66.

²⁹N. Spataru, T. N. Rao, D. A. Tryk, and A. Fujishima, J. Electrochem. Soc., 2001, 148, E112.

³⁰N. Spataru, B. V. Sarada, E. Popa, D. A. Tryk, and A. Fujishima, Anal. Chem., 2001, 73, 514.

³¹D. A. Tryk, K. Tsunozaki, T. N. Rao, and A. Fujishima, Diam. Relat. Mater., 2001, 10, 1804.

³²Y. C. Tsai, B. A. Coles, K. Holt, J. S. Foord, F. Marken, and R. G. Compton, Electroanalysis, 2001, 13, 831.

³³R. Uchikado, T. N. Rao, D. A. Tryk, and A. Fujishima, Chem. Lett., 2001, 144.

³⁴J. D. Wadhawan, F. J. Del Campo, R. G. Compton, J. S. Foord, F. Marken, S. D. Bull, S. G. Davies, D. J. Walton, and S. Ryley, J. Electroanal. Chem., 2001, 507, 135.

³⁵W. L. Wang, K. J. Liao, R. Q. Zhang, and C. Y. Kong, Materials Science and Engineering B-Solid State Materials for Advanced Technology, 2001, 85, 169.

³⁶J. Lee, D. A. Tryk, A. Fujishima, and S. M. Park, Chem. Commun., 2002, 486.

³⁷A. Manivannan, M. S. Seehra, D. A. Tryk, and A. Fujishima, Anal. Lett., 2002, 35, 355.

³⁸K. Ohnishi, Y. Einaga, H. Notsu, C. Terashima, T. N. Rao, S. G. Park, and A. Fujishima, Electrochem. Solid State Lett., 2002, 5, D1.

³⁹C. Prado, G. U. Flechsig, P. Grundler, J. S. Foord, F. Marken, and R. G. Compton, Analyst, 2002, 127, 329.

⁴⁰T. N. Rao, B. H. Loo, B. V. Sarada, C. Terashima, and A. Fujishima, Anal. Chem., 2002, 74, 1578.

⁴¹C. Terashima, T. N. Rao, B. V. Sarada, D. A. Tryk, and A. Fujishima, Anal. Chem., 2002, 74, 895.

⁴²J. van de Lagemaat, D. Vanmaekelbergh, and J. J. Kelly, J. Electroanal. Chem., 1999, 475, 139.

⁴³G. Pastor-Moreno and D. J. Riley, Electrochim. Acta, 2002, 47, 2589.

⁴⁴D. R. Lide, in 'CRC Handbook of Chemistry and Physics', ed. D. R. Lide, 1994.

⁴⁵T. N. Rao, D. A. Tryk, K. Hashimoto, and A. Fujishima, J. Electrochem. Soc., 1999, 146, 680.

⁴⁶S. Nakabayashi, N. Ohta, and A. Fujishima, PCCP, 1999, 1, 3993.

⁴⁷J. N. Chazalviel, J. Electrochem. Soc, 1982, 129, 923.

⁴⁸D. Vanmaekelbergh, Electrochim. Acta, 1997, 42, 1135.

⁴⁹D. Vanmaekelbergh, Electrochim. Acta, 1997, 42, 1121.

⁵⁰S. M. Sze, 'Semiconductor devices, physics and technology', ed. J. Wiley, 1985.

⁵¹G. M. Swain, J. Electrochem. Soc., 1994, 141, 3382.

⁵²R. Ramesham and M. F. Rose, Diam. Relat. Mater., 1997, 6, 17.

⁵³S. Yoshihara, K. Shinozaki, T. Zenbayashi, S. Morino, T. Shirakashi, K. Hashimoto, D. A. Tryk, and A. Fujishima, Electrochim. Acta, 2000, 45, 3375.

⁵⁴R. F. Mamin and T. Inushima, Synthetic Metals, 2001, 121, 1219.

⁵⁵R. F. Mamin and T. Inushima, Physical Review B, 2001, 6303, art. no.

⁵⁶C. E. Nebel, R. Zeisel, and M. Stutzmann, Diam. Relat. Mater., 2001, 10, 639.

⁵⁷M. A. Rodrigo, P. A. Michaud, I. Duo, M. Panizza, G. Cerisola, and C. Comninellis, J. Electrochem. Soc., 2001, 148, D60.

⁵⁸A. J. Saterlay, J. S. Foord, and R. G. Compton, Electroanalysis, 2001, 13, 1065.

⁵⁹J. M. Stotter, S. Haymond, J. E. Butler, G. M. Swain, and J. K. Zak, Abstracts of Papers of the American Chemical Society, 2001, 222, 117.

⁶⁰M. A. Witek and G. M. Swain, Abstracts of Papers of the American Chemical Society, 2001, 222, 59.

⁶¹M. A. Witek and G. M. Swain, Anal. Chim. Acta, 2001, 440, 119.

⁶²F. Marken, C. P. Paddon, and D. Asogan, Electrochem. Commun., 2002, 4, 62.

⁶³G. Pastor-Moreno and D. J. Riley, Electrochem. Commun., 2002, 4, 218.

⁶⁴C. Prado, S. J. Wilkins, F. Marken, and R. G. Compton, Electroanalysis, 2002, 14, 262.

⁶⁵I. Yagi, K. Tsunozaki, A. Fujishima, B. Ohtani, and K. Uosaki, J. Electrochem. Soc., 2002, 149, E1.