Chapter 9

 

Temperature modulated ac voltammetry

 

9.1. Introduction

 

Following the same line of investigation described in the chapter 8, small changes were introduced to perform ac voltammetry. Under potentiostatic conditions a range of voltages was applied and the change of the current at the electrode measured as the cell was illuminated by modulated radiation from an infrared diode. A new theory is presented that explains the obtained results.  As far the last chapter in which it was demonstrated how temocps allows impedance experiments to be performed without sophisticated equipment, the results obtain suggest that it is possible realise ac voltammetry studies using temperature modulation.

 

9.2. Theory

 

A theoretical development is required to describe how the changes in the temperature of the electrode cited in section 8.21 effects the current under potentiostatic conditions.

 

9.2.1. Relationship between the temperature and the constant applied potential

 

Considering the equivalent circuit shown below (Soret potential assumed to be zero)

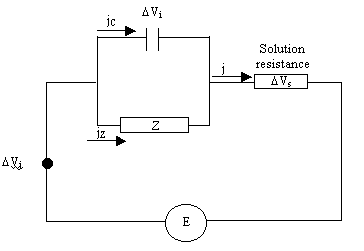
Figure 9.1. Equivalent model circuit

 

Either

                                                E = V_j + V_i + V_s                                 [equation 9.1]

 

or

                                                E = V_j + V_Z + V_s                                           [equation 9.2]

 

For a change in temperature DT the change in total potential is zero (potentiostatic control):

                                    DV_j + DV_i + DV_s = 0                                       [equation 9.3]

 

                                    DV_j + DV_Z + DV_s = 0                                      [equation 9.4]

 

From equations 8.32 and 8.44 equation 9.4 can be written as:

                                                              [equation 9.5]

 

Differentiating with respect to time yields:

 

                                                        [equation 9.6]

 

Applying Kirchoff´s law to the figure 9.1 gives

 

                                                            j_i + j_Z = j                                 [equation 9.7]

 

From equation 9.4

 

                                                DV_j + Z Dj_Z + R Dj = 0                       [equation 9.8]

 

Substituting equation 9.7 and 9.8 into 9.6 gives

 

                           [equation 9.9]

 Equation 9.9 shows the relationship between Dj and the temperature.

 

9.3. Experimental set-up

 

Electrochemical experiments were performed using a three electrode system. This section descibes the apparatus used.

 

9.3.1. Electrolyte solutions

 

18.3 MW cm ultrapure deionised water (Millipore) was used as solvent and 0.1  mol dm^-3 sulfuric acid (H₂SO₄) as supporting electrolyte.

 

Different solutions were prepared contaning:

 

·        1´10^-3 mol dm^-3 of ferrosulfate (Fe₂SO₄) / 1´10^-3 mol dm^-3 of ferricsulfate (Fe₂(SO₄)₃)  in 0.5 mol dm^-3 H₂SO₄ in H₂O.

 

·        2´10^-3 mol dm^-3 ferrosulfate/ 2´10^-3 mol dm^-3 of ferricsulfate in 0.5 mol dm^-3 H₂SO₄ in H₂O.

 

·        4´10^-3 mol dm^-3 ferrosulfate/ 4´10^-3 mol dm^-3 of ferricsulfate in 0.5 mol dm^-3 H₂SO₄ in H₂O.

 

·        6´10^-3 mol dm^-3 ferrosulfate/ 6´10^-3 mol dm^-3 of ferricsulfate in 0.5 mol dm^-3 H₂SO₄ in H₂O.

 

·        8´10^-3 mol dm^-3 ferrosulfate/ 8´10^-3 mol dm^-3 of ferricsulfate in 0.5 mol dm^-3 H₂SO₄ in H₂O.

 

Glassware was cleaned with a five step process (for further details see section 5.3.1)

 

All the solutions were purged with standard laboratoy grade oxygen-free argon (Ar) for aproximmately 30 minutes before any electrochemical experiment was performed.

 

9.3.2. Growing characteristics of the samples

 

In these studies the samples were the same as those used in the temperature modulation open circuit potential spectroscopy (for further details check section 8.3.3).

 

9.3.3. Working electrode construction and cell assembly

 

The construction process has been detailed in the section 8.3.4.

 

9.3.4. Counter Electrodes

 

The counter electrodes have been described in section 5.3.3.

 

9.3.5. Reference Electrodes

 

Reference electrodes used in these studies have been described in the section 8.3.6

 

9.3.6.   Faraday Cages

 

The Faraday cages have described in section 7.2.6.

 

9.3.7. Electronic equipment used in these studies

 

A light beam from 5mW infra red diode source was focused on the back of the gold diamond electrode. The light beam was modulated at 17.55 Hz using a lock in amplifier (Standford Research System Model SR830 DSP). The lock in amplifier fed with an ac (0.75 V) and dc (4.25V) sinusoidal component to the infrared diode. The fraction modulated in the light was 10 %. An in house built potentiostat was set up to drive the voltage for the system. After the beam irradiated the gold diamond electrode the electrochemical current response, in ac and dc terms, was analysed by the lock in amplifier. Phase angle and voltage responses for the different chosen potentials were recorded. The electrochemical glass cell operated in three electrode mode (gold diamond electrode as working electrode, a platinum counter electrode as counter electrode and a platinum wire as a pseudoreference electrode) (see figure 9.2). The cell assembly was housed in a Faraday cage to avoid any stray light or electrical pickup from external sources.

 

Cyclic voltammograms were measured with a using EG&G Princeton Applied Research Potentiostat/Galvanostat Model 273; controlled using Research Electrochemistry software (version 4.3).

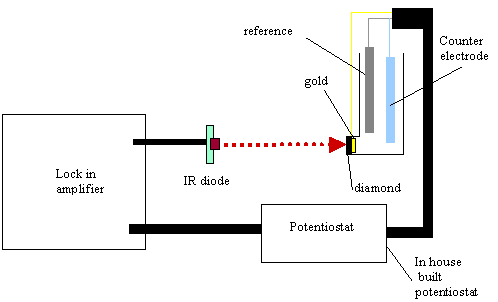
Figure 9.2. Experimental configuration to perform ac voltammetry.

 

9.4. Cyclic voltammograms

 

An i-E curve for a gold (on diamond substrate) electrode immersed in the 1´10^-3 mol dm^-3 of ferricsulfate (Fe₂(SO₄ )₃)/ 1´10^-3 mol dm^-3 of ferrosulfate (FeSO₄ ) in 0.5 mol dm^-3 H₂SO₄ aqueous solution is shown in the figure 9.3.

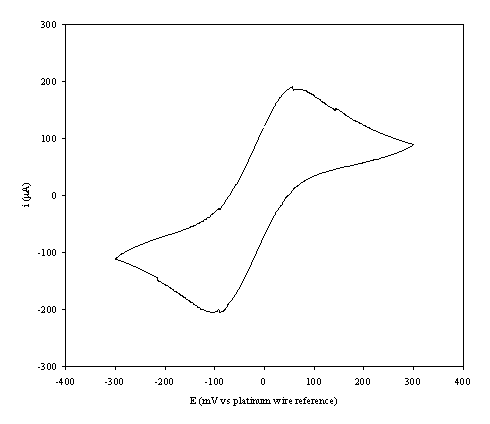
Figure 9.3. A cyclic voltammogram recorded at a gold (on diamond substrate) electrode immersed in 1´10^-3 mol dm^-3 of

ferricsulfate (Fe₂(SO₄ )₃)/ 1´10^-3 mol dm^-3 of ferrosulfate (FeSO₄ ) in 0.5mol dm^-3 H₂SO₄ aqueous solution. The i-E curve was recorded at scan rate of 0.1 V s^-1.

 

The curve shows a reversible reduction peak at -0.105 V and a reversible oxidation peak at 0.066 V that correspond with the formation of the species Fe⁺²/ Fe⁺³ respectively. The behaviour observed is the typical for the reduction of FeSO₄/Fe₂(SO₄)₃ in aqueous solvent (references). The differences between peak potentials (0.171 V) can be explained for the fact that the cyclic voltammogram was recorded in absence of iR compensation.

 

A cyclic voltammogram for each electrolyte concentration was recorded before any ac voltammetry experiments to ensure that the electrodes were functioning correctly.

 

A plot of the current height for the oxidation peak of each cyclic voltammogram was plotted against the concentration of the redox couple:

Figure 9.4. Oxidation current peaks against concentration of the ferrosulfate/ferricsulfate in 0.5 mol dm^-3 H₂SO₄.

 

A good linear relationship between the oxidation current and the concentration is apparent. This is in accordance with theory ^1-3.

9.5. Temperature modulation ac voltammetry experiments

 

Using the set up described in section 9.3.7 temperature modulation ac cyclic voltammograms were recorded for the different concentrations of ferricsulfate / ferrosulfate redox couple. Results are shown below in increasing order of concentration.

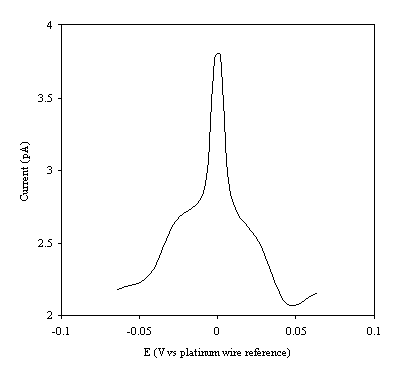
Figure 9.5. Current response of temperature modulation ac voltammetry against the applied potential referred to a platinum wire electrode for 1´ 10^-3 mol dm^-3 ferrosulfate (FeSO₄ )/ 1´ 10^-3 mol dm^-3 ferricsulfate (Fe₂(SO₄ )₃) in 0.5 mol dm^-3 H₂SO₄.

 

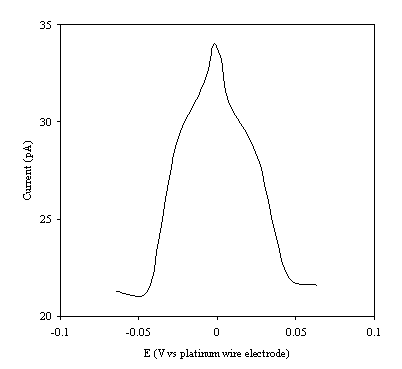
Figure 9.6. Current response of temperature modulation ac voltammetry against the applied potential referred to a platinum wire electrode for 2´ 10^-3 mol dm^-3 ferrosulfate (FeSO₄ )/ 2´ 10^-3 mol dm^-3 ferricsulfate (Fe₂(SO₄ )₃) in 0.5 mol dm^-3 H₂SO₄.

 

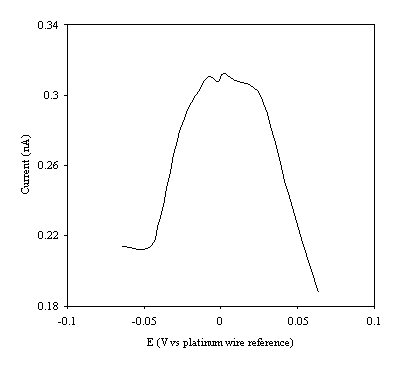
Figure 9.7. Current response of temperature modulation ac voltammetry against the applied potential referred to a platinum wire electrode for 4´ 10^-3 mol dm^-3 ferrosulfate (FeSO₄ )/ 4´ 10^-3 mol dm^-3 ferricsulfate (Fe₂(SO₄ )₃) in 0.5 mol dm^-3 H₂SO₄.

 

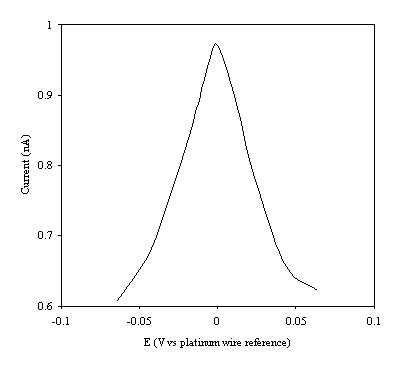
Figure 9.8. Current response of temperature modulation ac voltammetry against the applied potential referred to a platinum wire electrode for 6´ 10^-3 mol dm^-3 ferrosulfate (FeSO₄ )/ 6´ 10^-3 mol dm^-3 ferricsulfate (Fe₂(SO₄ )₃) in 0.5 mol dm^-3 H₂SO₄.

 

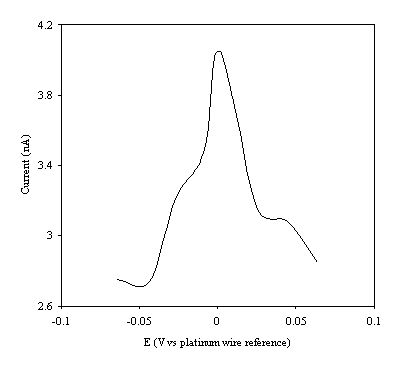
Figure 9.9. Current response of temperature modulation ac voltammetry against the applied potential referred to a platinum wire electrode for 8´ 10^-3 mol dm^-3 ferrosulfate (FeSO₄ )/ 8´ 10^-3 mol dm^-3 ferricsulfate (Fe₂(SO₄ )₃)in 0.5 mol dm^-3 H₂SO₄.

 

There is a common shape in all the plots. This general shape shows a high current at low values of voltage and then the current decreases as voltage tends towards the larger positive and negative values.

 

For further analysis of the temperature modulation ac voltammetries results adaptation in the mathematical development in section 9.2. The experimental set up is shown in figure 9.10.

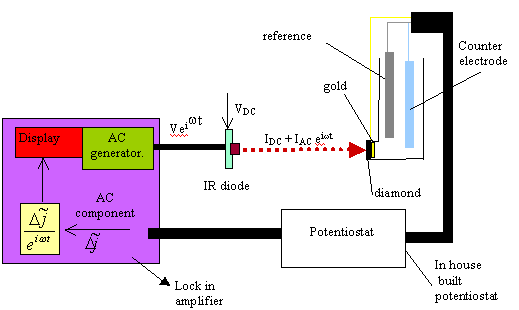
Figure 9.10. Diagram of the experimental set up that details the ac and dc components in the system.

 

From equation 8.55:

 

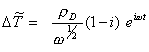                                  [equation 8.55]

 

Differentiating the above equation with respect to t yields

 

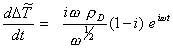                                                     [equation 8.56]

 

Substituting the equation 8.56 into equation 9.9 gives

 

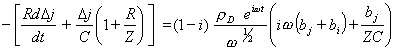
           [equation 9.10]

 

When solving equation 9.10 only the ac component is considered. The aim is to link the total current change with the applied potential in the experimental conditions.

 

Supposing that the total current change is due to a pure ac component then

 

       where S is an arbitrary parameter      [equation 9.11]

 

and differentiating equation 9.11 with respect to t yields

 

                                                                      [equation 9.12] 

 

Substituting equations 9.11 and 9.12 into equation 9.10 gives

 

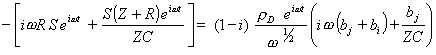
                                                                                                           [equation 9.13]

Rearranging the above equation S is obtained

 

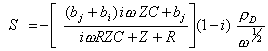                 [equation 9.14]

 

Therefore:

 

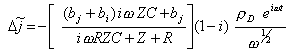            [equation 9.15]

The lock in measures                hence:

 

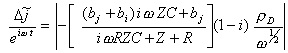            [equation 9.16]

 

At low frequency the interfacial impedance diffusion term is dominated by the Warburg element.  For a reversible system the Warburg element varies with potential¹  (note equation applies to only one redox species in solution alterations for two species will be small):

 

                                           [equation 9.17]

where a is

 

                                                        [equation 9.18]

 

and R is the gas constant. As in these studies a pseudoreference is used, E_1/2 is zero.  Also A, D and [O] should have the same length unit.

 

Mathcad 8 Profesional (MathSoft, Inc.) was operated to fit equation 9.16 with the experimental data. Parameters for the equation 9.16 were taken from different sources. Some of the parameters were deduced from the direct comparison between theoretical and experimental data. Others were taken from those employed in chapter 8.

 

Data from 4 ´10^-3 mol dm^-3 ferrosulfate/ ferricsulfate was chosen as the example to compare the experimental data with the theoretical one.

 

Parameters for the gold (on diamond substrate) electrode:

 

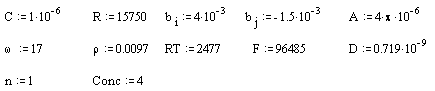
All the above parameters are in SI units.

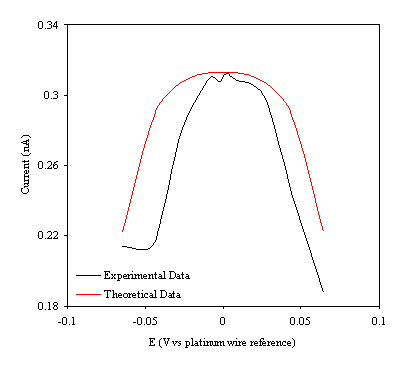
Figure 9.11. Current response of temperature modulation ac voltammetry against the applied potential referred to a platinum wire electrode for 4´ 10^-3 mol dm^-3 ferrosulfate (FeSO₄ )/ 4´ 10^-3 mol dm^-3 ferricsulfate (Fe₂(SO₄ )₃) in 0.5 mol dm^-3 H₂SO₄. Theoretical (in red line) and experimental (black line) are compared.

 

Figure 9.11 shows a reasonable agreement between the experimental and theoretical data. The theoretical data can only describe a symmetric ac voltammety function due to the simplifications of the mathematical development. However the theory indicates precisely the maximum of the ac voltammetry. The meaning of the theoretical ac voltammetry can be interpreted as the ideal limit of the ac voltammetry curve if the element Z of the equivalent circuit (figure 9.2) has transfer resistance component. In other words as if the only contribution of the impedance in the electrical circuit was coming from the Warburg element.

The shape of the curves suggests a description of the electrochemical system. At the electrode surface a continuous process of the ion transfer is occurring. When negative voltage are applied (see figure 9.11) the majority of the ions in the electrode surface are Fe²⁺. In this situation there is not enough supply of Fe³⁺ to permit a high reaction rate for the reversible electrode process that causes high impedance. When the impedance is high the ac current response is low. A similar situation can be explained when a positive voltage is applied. In this case the ion Fe³⁺ is at the electrode. There is not enough supply of Fe²⁺ to allow a high reaction for the reversible electrode process that causes high impedance. Then a low ac current respond is measured. When the maximum of the curves is reached in that situation, both ions Fe²⁺ and Fe³⁺ are approximately equally present at electrode surface. The reaction rate is high at the reversible electrode process giving low impedance. Therefore the ac current response is high (being the maximum value for the ac current response).

 

Some extra information from the theoretical fitting needs to be emphasised. A bigger electrical resistance (compared with the resistance values obtained in chapter 8) of the gold layer deposited on the diamond surface is necessary to fit the theoretical data with the experimental one. This fact can be explained if the electrical contact was not optimal to the gold layer. Higher resistance in the electrochemical cell, may be from the electrodes or from the electrolyte, could also explain the increase in the resistance.

 

The theoretical development suggests that the height of the peak using the temperature modulation technique for recording ac voltammetries should scale with the concentration. From the figures 9.5, 9.6, 9.7, 9.8 and 9.9 it is observed that the maximum of the ac voltammetry curves of the curve increase as the concentration does.

 

There is no doubt that the technique can be improved. A more detailed mathematical approach could be made in order to include the effect of the charge transfer resistance in the impedance element inside the electrical circuit. Certainly this will help to understand in deeper detail the changes in shape of the ac voltammetry curves as the concentration is increased. Analysis of further ac voltammetry studies at different frequencies will contribute more information about the behaviour of the electrochemical system. May be, as mentioned in  chapter 8, a power source of heating will reveal further details of the ac voltammetry using the temperature modulation technique.

 

Ac modulation techniques are generally used in analytical electrochemistry to measure very low concentrations. The temperature modulated method once optimised will possibly find uses in analysis.

 

9.6. Conclusions

 

A new method of ac voltammetry measurements has been developed using relatively simple equipment. This simplicity avoids the traditional limitations of more sophisticated apparatus allowing to perform ac voltammetry studies in one wide range of frequencies.  

 

9.7. References

 

¹              A. J. Bard and L. R. Faulkner, 'Electrochemical Methods Fundamentals and Applications', 2001.

²              A. C. Fischer, 'Electrode Dynamics', Oxford University Press, 1996.

³              S. R. Morrison, 'Electrochemistry at Semiconductor and Oxidized Metal Electrodes', Plenum Press, 1980.