Appendices

 

Appendix 1 :            Resonance-Enhanced Multiphoton Ionisation (REMPI) Spectroscopy

 

Multiphoton ionisation (MPI) techniques rely on a species absorbing a sufficient number of photons to exceed its ionisation energy, thereby forming an ion and an electron.  A biased probe wire or plate then detects either the ion or electron.  The probability that the ionisation process occurs is greatly enhanced if the absorption of an integer number of photons is resonant with a real excited electronic state of the neutral species (typically a Rydberg state).  This process allows the number of ions (or electrons) collected by a biased probe to be counted as a function of laser wavelength in order to produce a muliphoton ionisation spectrum.

 

REMPI schemes are typically written in the form (n + m) REMPI, where n signifies the number of photons used to promote the species into an eigenstate and m the number of further photons required to ionise the excited species, e.g. 2 +1 REMPI.  This technique is extremely species selective as a significant ionisation signal is only detected when the incident laser wavelength is tuned so that the process is resonance enhanced.

 

MPI also has the advantage that the selection rules for multiphoton excitation permit promotion into levels that are not normally accessible by one-photon excitation from the ground state.  The range of tunability of the laser is also multiplied by the number of photons required for the excitation of the Rydberg level, significantly broadening the spectral region that can be probed with a given laser.

 

REMPI provides a method of detecting non-fluorescing radicals such as CH₃, thought to be an important precursor for diamond growth, and therefore is a valuable diagnostic technique.

 

In the context of diamond CVD, REMPI has been previously used to observe H atoms and CH₃ radicals in a hot filament reactor.  However, the abundance of free electrons in microwave and DC-arcjet reactors prevent its use.

 

 

Appendix 2 :            Laser Induced Fluorescence (LIF) Spectroscopy

 

LIF techniques operate by detection of fluorescence from a species observed after excitation with a laser pulse.  The laser pulse, at a wavelength to coincide with absorption of the species, promotes the species into an excited state.  The consequent rapid fluorescent decay is detected with a photomultiplier tube, typically positioned at right angles to the incident laser beam.

 

Both the excitation and fluorescence wavelengths are species selective and the fluorescence signal is proportional to the population density in the excited state, and thus, in the absence of saturation effects, to the population in the initial state excited with the laser.

 

Tuning the laser wavelength therefore produces an excitation spectrum of the species of interest.  LIF is an unobtrusive, highly species selective technique that, with careful calibration, is capable of yielding absolute species number densities and is therefore considered to be ideal for monitoring species present in the highly volatile gas-phase environment typical in diamond CVD.  LIF techniques have previously been used to monitor CH, C₂ and C₂H in DC-arcjet reactors.

 

However, LIF techniques cannot detect non-fluorescing radicals.  The methyl radical, CH₃, cannot be detected by LIF due to the predissociative nature of its upper state, and has been detected via REMPI and CRDS.  It is also difficult to use in highly luminous environments, such as DC-arcjets.

 

 

Appendix 3 :            Cavity Ringdown Spectroscopy (CRDS)

 

CRDS is, in essence, a highly sensitive absorption technique.  The increased sensitivity over standard absorption techniques comes from augmenting the number of times the light passes through the absorbing medium, and measuring the change in the rate of light intensity decay as a function of time. In a traditional absorption experiment, depletion of the exciting light intensity is monitored.

 

Typical CRDS experiments use a pulsed tunable laser to pass light into a cavity, defined by two highly reflective (>99.5%) mirrors, and measure the decay of reflected light escaping from the exit mirror with a photomultiplier tube (PMT).  If the cavity contains a species that absorbs the radiation produced by the laser, the rate of decay will be faster than that of an empty (or non-absorbing) cavity.  The change in the decay trace coefficients may be used to calculate the absorption coefficient which, given the absorption cross section of the species of interest, may be used to obtain absolute column densities.  To obtain local concentrations one, of course, also needs an idea of the density profile along the column that is being probed.

 

In terms of diamond CVD, CRDS has previously been used successfully to monitor CH₃ radical number densities in a hot filament reactor.  As CRDS is capable of yielding absolute species number densities in a hostile environment, increased interest has recently been shown in this technique in the study of species in microwave or, as here, arcjet reactors.

 

 

Appendix 4 :            Optical emission spectroscopy (OES)

 

OES is used in the study of highly excited species that emit radiation in the wavelength range from the near UV to the near IR.  The high gas temperatures induce the spontaneous emission observed in DC-arcjet and microwave CVD reactors.  In such reactors the emission observed from H₂/CH₄ gas mixtures is mainly due to the C₂ Swan band system, the H-Balmer series and the A-X transition of CH.

 

This underlines the main limitation with OES measurements; that very few species transitions are detectable in the wavelength range that may be monitored conveniently.  This applies even to simple diatomic species like H₂ and ¹C₂.  Monitoring IR emission from vibrationally excited ground state species is another possibility, but quenching under typical process conditions is a problem, as is the spectral complexity given the high gas temperatures involved.

 

It is also relevant to note diamond growth is fundamentally achieved by species in their ground state.  OES, however, detects the decay from excited states.  Information from OES is thus relevant to diamond growth only if the correlation between ground and excited state species is established.  This said, OES has previously been used extensively in the detection of species in the diamond depositing gas-phase environment in microwave, DC-arcjet and hot filament reactors, not least for process control purposes.

 

Typically, emission from the gas-phase is passed through a monochromator.  Spectra are obtained either by rotating a diffraction grating and monitoring just the fraction of emission passing through the exit slit, or by collecting all the emission dispersed from the grating on a strip CCD detector.

 

OES has also proven useful in the determination of gas-phase temperatures in the CVD environment, with the rotational temperatures of C₂ and CH being calculated from the collected OES spectrum, assuming a Boltzmann population distribution over the various emitting rovibrational states.

 

 

Appendix 5 :            Saha Equation

 

The Saha equation describes the degree of different stages of ionization of a species under the assumption of Local Thermodynamic Equilibrium (LTE).

 

The equation allows for the fact that while the environment, theoretically, prevents the occurrence of species ionisation, the total number of free states is such that ionisation is promoted.

 

If we consider a system whereby the Boltzmann equation may be used to calculate the number density of ground state ionized atoms (n*), relative to ground state neutral atoms (n) then,

 

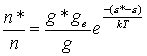
                                Equation A.1

 

where g* and g are the respective degeneracies of the ionised and neutral atoms, k is the Boltzmann constant, and the term (e*-e) describes the difference in energy between the atom and the ion.  The degeneracy (or statistical weight) of the free-electron state may be quoted as,

 

                                       Equation A.2

 

where m is the electron mass, n_e is the electron number density, u is the velocity of the electron and h is Planck’s constant.  Given that in equation A.1 the difference of energy between the atom and ion includes the ionization energy and the electron energy then,

 

                                         Equation A.3

 

where c is the ionization energy.  By combining equations A.1, A.2 and A.3 and integrating over all electron velocities the general Saha equation may be written as,

 

.                      Equation A.4

 

The Saha equation allows the state of the ionisation processes in a system to be calculated.  Examination of the equation also predicts a number of interesting features.  Firstly, the degree of ionisation in the system will be greater than that predicted by calculations based on the local gas temperature and the species ionisation potential.  Secondly, since, in general, the ground state of the ion lies well below the various excited states, the ions produced are predominantly in their ground state.

 

However, the Saha equation assumes LTE, which is considered unlikely in the diamond CVD environment, this therefore causes the limitation that it is strictly only applicable if elastic collisions are responsible for establishing the energetic distribution of particles.  In most practical cases radiative processes will be more important, and an explicit detailed equilibrium calculation is necessary in order to determine the distribution of electrons over the various energya-levels.

 

Appendix 6 : GRI_MECH 3.0 (C / H / N) Gas-phase chemistry

 

This table shows all reactions used in the numerical simulations detailed in the modelling of a HF-CVD reactor operating on a CH₄/NH₃/H₂ gas mixture, with all irrelevant reactions removed, i.e. those involving oxygen or argon.  The reaction rate co-efficients shown are such that the reaction rate constant, k, may be calculated from,

 

.                                          Equation A.5

 

The coefficients listed here have the units; A (cm³ mol^-1s^-1), b is dimensionless and E_a (cal mol^-1K^-1).  The entire mechanism is shown here, where M signifies a third body.  For such three body reactions, the following three lines detail the relative third body efficiencies.  The prefix LOW or TROE designates a set of constants that describe respectively, the falloff rates for low-pressure rate limits, and the falloff form to describe pressure effects as presented by J. Troe†.

 

 

Reaction                                                                        A                      b                     E_a

2H+M<=>H2+M                              1.000E+18   -1.000       .00

H2/ .00/ CH4/2.00/ C2H6/3.00/

 

2H+H2<=>2H2                              9.000E+16    -.600       .00

 

H+CH<=>C+H2                              1.650E+14     .000       .00

 

H+CH2(+M)<=>CH3(+M)                      6.000E+14     .000       .00

     LOW  /  1.040E+26   -2.760   1600.00/

     TROE/   .5620  91.00  5836.00  8552.00/

H2/2.00/ CH4/2.00/ C2H6/3.00/

 

H+CH2(S)<=>CH+H2                         3.000E+13     .000       .00

 

H+CH3(+M)<=>CH4(+M)                      13.90E+15    -.534    536.00

     LOW  /  2.620E+33   -4.760   2440.00/

     TROE/   .7830   74.00  2941.00  6964.00 /

H2/2.00/ CH4/3.00/ C2H6/3.00/

 

H+CH4<=>CH3+H2                           6.600E+08    1.620  10840.00

 

H+C2H(+M)<=>C2H2(+M)                     1.000E+17   -1.000       .00

     LOW  /  3.750E+33   -4.800   1900.00/

     TROE/   .6464  132.00  1315.00  5566.00 /

H2/2.00/ CH4/2.00/ C2H6/3.00/

 

H+C2H2(+M)<=>C2H3(+M)                    5.600E+12     .000   2400.00

     LOW  /  3.800E+40   -7.270   7220.00/

     TROE/   .7507   98.50  1302.00  4167.00 /

H2/2.00/ CH4/2.00/ C2H6/3.00/

 

H+C2H3(+M)<=>C2H4(+M)                    6.080E+12     .270    280.00

     LOW  /  1.400E+30   -3.860   3320.00/

     TROE/   .7820  207.50  2663.00  6095.00 /

H2/2.00/ CH4/2.00/ C2H6/3.00/

H+C2H3<=>H2+C2H2                         3.000E+13     .000       .00

 

H+C2H4(+M)<=>C2H5(+M)                    0.540E+12     .454   1820.00

     LOW  /  0.600E+42   -7.620   6970.00/

     TROE/   .9753  210.00   984.00  4374.00 /

H2/2.00/ CH4/2.00/ C2H6/3.00/

 

H+C2H4<=>C2H3+H2                         1.325E+06    2.530  12240.00

 

H+C2H5(+M)<=>C2H6(+M)                    5.210E+17    -.990   1580.00

     LOW  /  1.990E+41   -7.080   6685.00/

     TROE/   .8422  125.00  2219.00  6882.00 /

H2/2.00/ CH4/2.00/ C2H6/3.00/

 

H+C2H5<=>H2+C2H4                         2.000E+12     .000       .00

 

H+C2H6<=>C2H5+H2                         1.150E+08    1.900   7530.00

 

C+CH2<=>H+C2H                            5.000E+13     .000       .00

 

C+CH3<=>H+C2H2                           5.000E+13     .000       .00

 

CH+H2<=>H+CH2                            1.080E+14     .000   3110.00

 

CH+CH2<=>H+C2H2                          4.000E+13     .000       .00

 

CH+CH3<=>H+C2H3                          3.000E+13     .000       .00

 

CH+CH4<=>H+C2H4                          6.000E+13     .000       .00

 

CH2+H2<=>H+CH3                           5.000E+05    2.000   7230.00

 

2CH2<=>H2+C2H2                           1.600E+15     .000  11944.00

 

CH2+CH3<=>H+C2H4                         4.000E+13     .000       .00

 

CH2+CH4<=>2CH3                           2.460E+06    2.000   8270.00

 

CH2(S)+H2<=>CH3+H                        7.000E+13     .000       .00

 

CH2(S)+CH3<=>H+C2H4                      1.200E+13     .000   -570.00

 

CH2(S)+CH4<=>2CH3                        1.600E+13     .000   -570.00

 

CH2(S)+C2H6<=>CH3+C2H5                   4.000E+13     .000   -550.00

 

2CH3(+M)<=>C2H6(+M)                      6.770E+16   -1.180    654.00

     LOW  /  3.400E+41   -7.030   2762.00/

     TROE/   .6190  73.20  1180.00  9999.00 /

H2/2.00/ CH4/2.00/ C2H6/3.00/

 

2CH3<=>H+C2H5                            6.840E+12     .100  10600.00

 

CH3+C2H4<=>C2H3+CH4                      2.270E+05    2.000   9200.00

 

CH3+C2H6<=>C2H5+CH4                      6.140E+06    1.740  10450.00

 

C2H+H2<=>H+C2H2                          5.680E+10    0.900   1993.00

 

C2H4(+M)<=>H2+C2H2(+M)                   8.000E+12     .440  86770.00

     LOW  /  1.580E+51   -9.300  97800.00/

     TROE/   .7345  180.00  1035.00  5417.00 /

H2/2.00/ CH4/2.00/ C2H6/3.00/

 

CH+H2(+M)<=>CH3(+M)                      1.970E+12     .430   -370.00

   LOW/ 4.820E+25  -2.80  590.0 /

   TROE/ .578  122.0  2535.0  9365.0 /

H2/2.00/ CH4/2.00/ C2H6/3.00/

 

CH2+CH2=>2H+C2H2                         2.000E+14     .000  10989.00

 

CH3+C2H5(+M)<=>C3H8(+M)                  .9430E+13     .000       .00

     LOW/ 2.710E+74  -16.82  13065.0 /

     TROE/ .1527  291.0  2742.0  7748.0 /

H2/2.00/ CH4/2.00/ C2H6/3.00/

 

H+C3H8<=>C3H7+H2                         1.320E+06    2.540   6756.00

 

CH3+C3H8<=>C3H7+CH4                      0.903E+00    3.650   7154.00

 

CH3+C2H4(+M)<=>C3H7(+M)                  2.550E+06    1.600   5700.00

      LOW/ 3.00E+63  -14.6  18170./

      TROE/ .1894  277.0  8748.0  7891.0 /

H2/2.00/ CH4/2.00/ C2H6/3.00/

 

H+C3H7(+M)<=>C3H8(+M)                    3.613E+13     .000       .00

      LOW/ 4.420E+61  -13.545  11357.0/

      TROE/ .315  369.0  3285.0  6667.0 /

H2/2.00/ CH4/2.00/ C2H6/3.00/

 

H+C3H7<=>CH3+C2H5                        4.060E+06    2.190    890.00

 

CH3+C3H7<=>2C2H5                         1.927E+13   -0.320       .00

 

NH+H<=>N+H2                              3.200E+13     .000    330.00

 

NH+N<=>N2+H                              1.500E+13     .000       .00

 

NH2+H<=>NH+H2                            4.000E+13     .000   3650.00

 

NNH<=>N2+H                               3.300E+08     .000       .00

 

NNH+M<=>N2+H+M                           1.300E+14    -.110   4980.00

H2/2.00/ CH4/2.00/ C2H6/3.00/

 

NNH+H<=>H2+N2                            5.000E+13     .000       .00

 

NNH+CH3<=>CH4+N2                         2.500E+13     .000       .00

 

CN+H2<=>HCN+H                            2.950E+05    2.450   2240.00

 

HCN+M<=>H+CN+M                           1.040E+29   -3.300  26600.00

H2/2.00/ CH4/2.00/ C2H6/3.00/

 

H+HCN(+M)<=>H2CN(+M)                     3.300E+13     .000       .00

      LOW /  1.400E+26   -3.400    1900.00/

H2/2.00/ CH4/2.00/ C2H6/3.00/

 

H2CN+N<=>N2+CH2                          6.000E+13     .000    400.00

 

C+N2<=>CN+N                              6.300E+13     .000  46020.00

 

CH+N2<=>HCN+N                            3.120E+09    0.880  20130.00

 

CH+N2(+M)<=>HCNN(+M)                     3.100E+12     .150       .00

     LOW  /  1.300E+25   -3.160    740.00/

     TROE/   .6670  235.00  2117.00  4536.00 /

H2/2.00/ CH4/2.00/ C2H6/3.00/

 

CH2+N2<=>HCN+NH                          1.000E+13     .000  74000.00

 

CH2(S)+N2<=>NH+HCN                       1.000E+11     .000  65000.00

 

HCNN+H<=>CH2+N2                          1.000E+14     .000       .00

 

CH3+N<=>H2CN+H                           6.100E+14    -.310    290.00

 

CH3+N<=>HCN+H2                           3.700E+12     .150    -90.00

 

NH3+H<=>NH2+H2                           5.400E+05    2.400   9915.00

 

 

Appendix 7 : Laser Raman Spectroscopy (LRS)

 

If monochromatic radiation is passed through a substance most of the scattered radiation will be of the incident frequency (Rayleigh Scattering).  However, certain discrete frequencies above and below that of the incident radiation (Raman scattering) will also be present.  Elastically and inelastically scattered photons are detected with energies of, hn and hn ± DE, where n is the frequency of the incident beam.

 

The inelastically scattered photons, having exchanged energy with the sample, will be of frequency, n ±DE/h, where DE coincides with a vibrational (or rotational) transition in the case of an isolated molecule, or a phonon mode in the case of a solid.  If the sample gains energy the scattered photon will be of frequency, n -DE/h this is known as Stokes’ radiation.  Conversely, if the sample loses energy the scattered photon is known as anti-Stokes’ radiation, (i.e. n +DE/h).

 

In the context of diamond analysis, LRS is an important technique as the vibrational modes within the bulk crystal are sensitive to the nature of the bonding.  LRS is capable of showing both sp³ bonded carbon (sharp Raman peak centred at ~1333 cm^-1) typical of diamond, and sp² graphitic carbon (broad Raman peak centred around 1550 cm^-1).  Therefore LRS has become useful as a diagnostic tool for, as-grown CVD diamond films, providing information of the diamond/graphitic content.