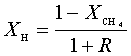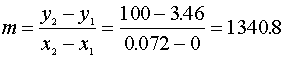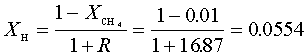Chapter 8 - CHEMKIN Simulations

8.1 Introduction

In-situ molecular beam mass spectrometry (MBMS) of diamond CVD environments has proved both useful and versatile in its application. However, detailed numerical modelling of the CVD gaseous environment can serve not only as a useful complement to experimental studies but also as an important instrument to test the validity of the MBMS results. To develop such a modelling system is not trivial by any means since chemical reaction mechanisms containing hundreds of reactions and involving 50 or more chemical species are common in the diamond CVD process. Thus there is a need for accurate, detailed descriptions of the chemical kinetics occurring in the gas-phase and/or on reactive surfaces, in order to perform a complete simulation of the diamond growth process.

In the present study, a highly structured computer package called CHEMKIN^8.1 has been employed to aid in the incorporation of a complex gas-phase chemical reaction mechanism into numerical simulations. Such a package has already been utilised by several groups^8.2-8.7 as a means of characterising the diamond growth environment using different source gas mixtures. Particularly beneficial to the present work is the capacity to calculate concentrations of free radicals as well as stable species, provided the necessary input data relevant to the species is given to complement the measured concentrations of the stable species.

8.2 Structure of CHEMKIN

CHEMKIN is a highly structured package that requires the manipulation of a number of programs, subroutines, and data files. Figure 8.1 shows a schematic diagram of the general structure of the CHEMKIN package. It is composed of four important pieces: the Interpreter, the Thermodynamic Database, the Linking File and the Gas-Phase Subroutine Library.

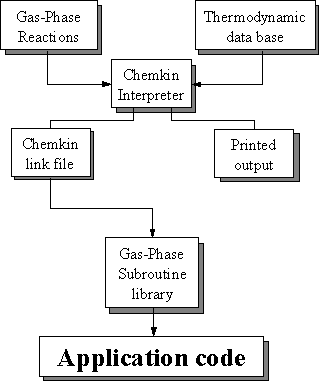
Figure 8.1. Structure of the CHEMKIN package and its link to an application code (adapted from Reference 8.1).

The Interpreter is a program that first reads the user’s symbolic description of the reaction mechanism, where the pre-exponential factor A_i (units - cm-mol-s-K) , the temperature exponent b_i, and the activation energy E_i (units - cal/mol) are specified (See Figure 8.2).

Consider the rate law for the consumption of reactant A as:

where k is the rate constant, and the reaction is second order overall, but first order in each of two reactants A and B. The rate constant, k, is related to the pre-exponential factor A, the temperature exponent b, and the activation energy E via

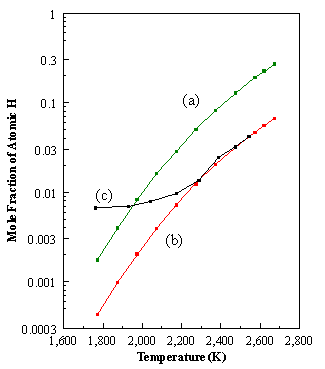
In the above rate law k will have units:

k = cm³mol^-1s^-1

and so the units of the pre-exponential factor, A, will be written as cm³mol^-1s^-1. However, we parametise the traditional A factor to include a temperature-dependent term, i.e. A_iT^b. This term will therefore have units cm³ mol^-1s^-1. So if b = 1, for example, then A_i will have units mol^-1cm³s^-1K^-1. Clearly if b is non-integer then the units of A_i will be mol^-1cm³s^-1K^-^b.

Having read the symbolic description of the reaction mechanism the CHEMKIN package then extracts thermodynamic information for the relevant species from the Thermodynamic Data Base.^8.8 The information in the database can be added or modified by input to the Interpreter (See Figure 8.3). The thermodynamic data are stored as polynomial fits to specific heat c_p/R, enthalpy H⁰/RT, and entropy S⁰/R. There are seven coefficients for each of two temperature ranges.

(1)

(2)

(3)

Thus for each species there are 14 coefficients in all. In addition to the polynomial coefficients for each species, the Thermodynamic Data Base provides the species name, its elemental make-up, and the temperature ranges over which the fits are valid.

Essentially the thermodynamic database is a table of specific heat, enthalpy, and entropy as a function of temperature. In addition, since the fits span two temperature ranges, the temperature ranges have to be specified. A common temperature is used which connects the two ranges, typically 1000K, but it may be different in some cases. An illustration of the thermodynamic data format is shown below.

! CHEM.INP Figure 8.2. The input file used by the

! Input file for CHEMKIN interpreter. Interpreter in this present study. The

ELEMENTS gas phase reactions was obtained

C H from Refs. 8.9, 8.10 and 8.11

END

SPECIES

CH4 CH3 CH2 CH C

C2H6 C2H5 C2H4 C2H3 C2H2 C2H

H H2

END

REACTIONS

! ---------------------------------HYDROGEN REACTIONS------------------------------

H+H+M=H2+M 9.7E+16 -0.6 0

! --------------------------------------C-1 REACTIONS--------------------------------------

CH3+H+M=CH4+M 8.0E+26 -3.0 0

CH4+H=CH3+H2 2.2E+04 3.0 8800

CH4+CH2=CH3+CH3 1.0E+13 0.0 0

CH3+CH3=C2H5+H 2.8E+13 0.0 13600

CH3+CH3+M=C2H6+M 3.2E+41 -7.0 2766

CH3+H=CH2+H2 7.2E+14 0.0 15100

CH3+CH2=C2H4+H 2.0E+13 0.0 0

CH3+M=CH2+H+M 1.0E+16 0.0 90600

CH2+H=CH+H2 4.0E+13 0.0 0

CH+CH4=C2H4+H 6.0E+13 0.0 0

CH+CH3=C2H3+H 3.0E+13 0.0 0

CH+H=C+H2 1.5E+14 0.0 0 !C+F 92:145-160

CH+CH2=C2H2+H 4.0E+13 0.0 0 !C+F 92:145-160

C+CH3=C2H2+H 5.0E+13 0.0 0 !C+F 92:145-160

C+CH2=C2H+H 5.0E+13 0.0 0 !C+F 92:145-160

! -------------------------------------C-2 REACTIONS--------------------------------------

C2H6=CH3+CH3 9.4E+45 -9.0 100700

C2H6+H=C2H5+H2 5.4E+02 3.5 5210 !C+F 92:419-439

C2H6+CH3=C2H5+CH4 5.5E-01 4.0 8300

C2H5+M=C2H4+H+M 1.0E+17 0.0 31000

C2H5+CH3=C2H4+CH4 7.9E+11 0.0 0

C2H4+M=C2H2+H2+M 2.6E+17 0.0 79400

C2H4+M=C2H3+H+M 2.6E+17 0.0 96600

C2H4+H=C2H3+H2 1.1E+14 0.0 8500 !C+F 92:419-439

C2H4+CH3=CH4+C2H3 4.2E+11 0.0 11200

C2H3+H=C2H2+H2 2.0E+13 0.0 0

C2H3+M=C2H2+H+M 3.0E+15 0.0 32000

C2H3+CH3=C2H2+CH4 7.9E+11 0.0 0

C2H2+M=C2H+H+M 4.0E+16 0.0 107000

C2H2+H=C2H+H2 6.0E+13 0.0 23700

C2H2+CH3=C2H3+CH2 3.1E+14 0.0 69888 !C+F 92:419-439

C2H2+C2H2=C2H3+C2H 3.1E+14 0.0 91208 !C+F 92:419-439

C2H2+CH2=C2H3+CH 1.5E+14 0.0 62636 !C+F 92:419-439

C2H2+H2=CH2+CH2 7.1E+15 0.0 127788 !C+F 92:419-439

END

Name

species

CH₄

Date ¬ atomic phase

symbols of

& species

formula ®

121286C 1H 4 G

low high common

temp. temp. temp.

(K) (K) (K)

0300.00 5000.00 1000.00

Line

number

a₁

0.01683478E+02

a₂

0.10237236E-01

a₃

-0.03875128E-04

a₄

0.06785585E-08

a₅

-0.04503423E-12

a₆

-0.10080787E+05

a₇

0.09623395E+02

a₁

0.07787415E+01

a₂

0.01747668E+00

a₃

-0.02783409E-03

a₄

0.03049708E-06

a₅

-0.12239307E-10

a₆

-0.09825229E+05

a₇

0.13722195E+02

Figure 8.3. Format for thermodynamic data. The first seven coefficients in the polynomial expansion are for the upper temperature interval. The final seven coefficients in the polynomial expansion are for the lower temperature interval.

In addition to printed output, the Interpreter writes a Linking File, which contains all the pertinent information on the elements, species, and reactions in the mechanism. Once the Interpreter has been executed and the Linking File created, the Gas-Phase Subroutine Library can be used. These subroutines are called from the Fortran code. The CHEMKIN gas-phase subroutines, of which there are over 100, are called as required to return information on the elements, species, reactions, equations of state, thermodynamic properties and chemical production rates. In general the input to these routines is the state of the gas-pressure or density, temperature, and the species composition. The code is designed to facilitate selection of the particular CHEMKIN subroutines that are needed for a given problem.

8.3 Structure of the Transport Property Fitting Code and SURFACE CHEMKIN

Since the diamond CVD process not only involves gas-phase reactions mechanism but also heterogeneous gas-solid reactions occurring on the substrate and the various transport processes, the CHEMKIN package alone cannot fully simulate the growth process. The Transport package and SURFACE CHEMKIN^8.12 are therefore introduced as another component of a large body of software designed to facilitate the computational modelling of chemical kinetics in flowing systems such as diamond CVD. Figure 8.4 shows how these packages are linked and used in the present study to simulate the diamond CVD process.

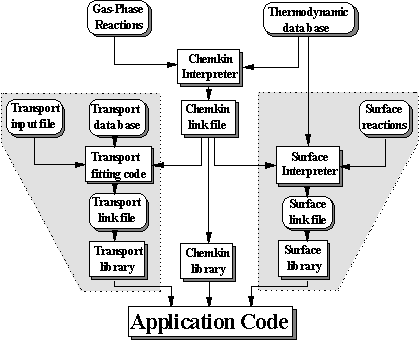
Figure 8.4. Relationships and flow of information between the CHEMKIN, Transport, and SURFACE CHEMKIN packages, and a user’s application code (adapted from Reference 8.12).

The Transport package handles the gas-phase molecular transport properties and SURFACE CHEMKIN handles the surface thermodynamics and chemical kinetics. Each package consists of an Interpreter, a database of either thermodynamic or transport properties, and a library of subroutines that can be called from the application code.

In the case of diamond CVD, since the surface chemistry involves gas-solid heterogeneous reactions, the first step is to run the CHEMKIN Interpreter, which reads the user’s description of the gas-phase reaction mechanism (Figure 8.2). The Linking file is read by the Gas-Phase Subroutine Library that makes the information available to all the other subroutines in the library.

The next step is to execute the SURFACE CHEMKIN Interpreter, which reads the user’s symbolic description of the surface reaction mechanism. Required thermodynamic data can come from the same Thermodynamic Database used by CHEMKIN or from a separate Thermodynamic Database compiled for surface reactions. As Figure 8.5 shows, the thermodynamic data have been added by input into the Interpreter. The SURFACE CHEMKIN Interpreter extracts all needed information about gas-phase species from the CHEMKIN Linking File. Like the CHEMKIN Interpreter, the SURFACE CHEMKIN Interpreter also provides a printed output and a Linking File. Again the Surface Linking File is read by a subroutine in the Surface Subroutine Library that makes the surface reaction mechanism information available to all other subroutines in the library.

Finally, the Transport Property Fitting Code reads the CHEMKIN Linking File and identifies all the gas-phase species that are present in the gas-phase reaction mechanism. Then, drawing on a database of molecular parameters, it computes the species’ viscosities, thermal conductivities, and diffusion coefficients. As with the other packages it provides a Linking File that is read by a subroutine in the Transport Property Subroutine Library. Subroutines from this library may be called by the application code to return transport properties for individual species or for a multicomponent gas mixture.

! SURF.INP

! Input file for SURFACE interpreter.

! SURFACE SITES & SPECIES.

! Density of 5.22E-09 mol/cm2 corresponding to sites on the (111) surface of diamond.

SITE/DIAMOND/ SDEN/5.22E-09/

CH(S) C(S,R) C(R,G) C(S,R3) HCCH(S,R)

CH2(S) CH(S,R) CH(S,G) CH(S,R2) H2CCH(S)

CH3(S) CH2(S,R) CH2*(S)

END

BULK

D /3.515/

G /3.515/

END

! THERMODYNAMIC DATA.

! Taken from Tables III and IV of Reference 8.13

THERMO ALL

300. 1000. 3000.

CH(S) 050595C 1H 1 0 0G 300.00 3000.00 1000.00 1

0.14872259E+01 0.33000924E-02 -0.28411702E-06 -0.34383971E-09 0.76660243E-13 2

-0.05865759E+04 -0.09239365E+02 0.14872259E+01 0.33000924E-02 -0.28411702E-06 3

-0.34383971E-09 0.76660243E-13 -0.05865759E+04 -0.09239365E+02 4

C(S,R) 050595C 1 0 0 0G 300.00 3000.00 1000.00 1

0.16900997E+01 0.11069085E-02 -0.12616481E-06 0.11996654E-09 0.28811839E-13 2

0.02130371E+06 -0.09750481E+02 0.16900997E+01 0.11069085E-02 -0.12616481E-06 3

-0.11996654E-09 0.28811839E-13 0.02130371E+06 -0.09750481E+02 4

C(S,R3) 100191C 1 0 0 0G 300.00 3000.00 1000.00 1

0.16900997E+01 0.11069085E-02 -0.12616481E-06 -0.11996654E-09 0.28811839E-13 2

0.64193504E+05 -0.10340458E+02 -0.12628431E+01 0.73135700E-02 -0.72650602E-06 3

-0.57274971E-08 0.29829661E-11 0.65054285E+05 0.52818985E+01 4

CH(S,R2) 062992C 1H 1 I 300.00 3000.00 1000.00 1

0.14872311E+01 0.33000871E-02 -0.28411483E-06 -0.34383973E-09 0.76660114E-13 2

0.43930898E+05 -0.10147053E+02 -0.18659885E+01 0.90232668E-02 0.29341194E-06 3

-0.52555555E-08 0.20408896E-11 0.45065105E+05 0.81504097E+01 4

CH(S,G) 050792C 1H 1 I 300.00 3000.00 1000.00 1

0.14817694E+01 0.32751665E-02 -0.27781763E-06 -0.34004749E-09 0.75557168E-13 2

0.10660619E+05 -0.10097240E+02 -0.18745055E+01 0.90725571E-02 0.24365704E-06 3

-0.53500671E-08 0.21229865E-11 0.11787394E+05 0.81871119E+01 4

HCCH(S,R) 071291C 2H 2 0 0G 300.000 3000.000 1000.00 1

0.17394471E+01 0.51764320E-02 -0.42153641E-06 -0.53463645E-09 0.11763388E-12 2

-0.59624932E+04 -0.12329198E+02 -0.25071146E+01 0.12199585E-01 0.59056043E-06 3

-0.66420434E-08 0.24363521E-11 -0.45017656E+04 0.10931940E+02 4

CH2(S) 050595C 1H 2 0 0G 300.00 3000.00 1000.00 1

0.17394471E+01 0.51764320E-02 -0.42153641E-06 -0.53463645E-09 0.11763388E-12 2

-0.06534599E+05 -0.11177380E+02 0.17394471E+01 0.51764320E-02 -0.42153641E-06 3

-0.53463645E-09 0.11763388E-12 -0.06534599E+05 -0.11177380E+02 4

CH(S,R) 050595C 1H 1 0 0G 300.00 3000.00 1000.00 1

0.14872259E+01 0.33000924E-02 -0.28411702E-06 -0.34383971E-09 0.76660243E-13 2

0.01547748E+06 -0.09239365E+02 0.14872259E+01 0.33000924E-02 -0.28411702E-06 3

-0.34383971E-09 0.76660243E-13 0.01547748E+06 -0.09239365E+02 4

C(R,G) 050792C 1 I 300.00 3000.00 1000.00 1

0.16900998E+01 0.11069081E-02 -0.12616400E-06 -0.11996697E-09 0.28811900E-13 2

0.35690953E+05 -0.10340459E+02 -0.12628419E+01 0.73135681E-02 -0.72650272E-06 3

-0.57275016E-08 0.29829680E-11 0.36551734E+05 0.52818918E+01 4

H2CCH(S) 071291C 2H 3 0 0G 300.00 3000.00 1000.00 1

0.36940942E+01 0.79702111E-02 -0.64374024E-06 -0.81818519E-09 0.17982379E-12 2

0.14525338E+05 -0.24731092E+02 -0.43835902E+01 0.23068689E-01 -0.28454056E-0 3

-0.14521289E-07 0.65029358E-11 0.17095203E+05 0.18776432E+02 4

CH3(S) 050595C 1H 3 0 0G 300.00 3000.00 1000.00 1

0.22271934E+01 0.64840489E-02 -0.50900690E-06 -0.66263206E-09 0.14445464E-12 2

0.07774954E+05 -0.14189754E+02 0.22271934E+01 0.64840489E-02 -0.50900690E-06 3

-0.66263206E-09 0.14445464E-12 0.07774954E+05 -0.14189754E+02 4

CH2(S,R) 050595C 1H 2 0 0G 300.00 3000.00 1000.00 1

0.17394471E+01 0.51764320E-02 -0.42153641E-06 -0.53463645E-09 0.11763388E-12 2

0.02478779E+06 -0.11177380E+02 0.17394471E+01 0.51764320E-02 -0.42153641E-06 3

-0.53463645E-09 0.11763388E-12 0.02478779E+06 -0.11177380E+02 4

CH2*(S) 071291C 1H 2 0 0G 300.00 3000.00 1000.00 1

0.17394471E+01 0.51764320E-02 -0.42153641E-06 -0.53463645E-09 0.11763388E-12 2

-0.59624932E+04 -0.12329198E+02 -0.25071146E+01 0.12199585E-01 0.59056043E-06 3

-0.66420434E-08 0.24363521E-11 -0.45017656E+04 0.10931940E+02 4

D 051795C 1 S 300.00 3000.00 1000.00 1

0.16900997E+01 0.11069085E-02 -0.12616481E-06 -0.11996654E-09 0.28811839E-13 2

-0.02996751E+04 -0.09755593E+02 0.16900997E+01 0.11069185E-02 -0.12616481E-06 3

-0.11996654E-09 0.28811839E-13 -0.02996751E+04 -0.09755593E+02 4

G 071291C 1 0 0 0G 300.00 3000.00 1000.00 1

0.16900997E+01 0.11069085E-02 -0.12616481E-06 -0.11996654E-09 0.28811839E-13 2

-0.79270331E+03 -0.10340458E+02 -0.12628431E+01 0.73135700E-02 -0.72650602E-06 3

-0.57274971E-08 0.29829661E-11 0.68074341E+02 0.52818985E+01 4

END

! GAS-SURFACE REACTION MECHANISM.

! Incorporating: activation of surface by H atoms; recombination of H on the surface;

! chemisorption of CH3 radicals onto activated sites; incorporation of these molecules into

! the diamond structure (See Reference 8.13).

REACTIONS

! New Chlorine Chemistry

CH(S) +CL <=> C(S,R) + HCL 0.5032 0.0 1000.0

STICK

CH2(S) +CL <=> CH(S,R) + HCL 0.5032 0.0 1000.0

STIC

CH3(S) +CL <=> CH2(S,R) + HCL 1.00 0.0 1000.0

STICK

! Initiation Reaction

CH(S) +H <=> C(S,R) + H2 2.14 0.0 7300.0

STICK

! Surface H Replenishing

C(S,R) + H <=> CH(S) 0.3 0.0 0.0

STICK

! Methyl Addition Reactions

C(S,R) + CH3 <=> D + CH3(S) 0.33 0.0 0.0

STICK

CH2(S) + H <=> CH(S,R) + H2 2.14 0.0 7300.0

STICK

CH3(S) + H <=> CH2(S,R) + H2 4.28 0.0 7300.0

STICK

CH2(S,R) + CH(S,R) <=> CH2(S) + CH(S) 6.0E+19 0.0 0.0

! Acetylene Addition Reactions

C(S,R) + C2H2 <=> D + HCCH(S,R) 8.0E10 0.0 7700.0

CH(S) + HCCH(S,R) <=> C(S,R) + H2CCH(S) 6.0E19 0.0 0.0

H2CCH(S) + C(S,R) <=> D + CH2(S)+CH(S,R) 6.0E19 0.0 0.0

CH2(S) + CH(S,R) <=> CH2*(S)+ CH(S,R) 6.0E19 0.0 2122.0

CH(S,R) + H + CH2*(S) <=> CH(S) + CH(S) + H2 2.14 0.0 7300.0

! Carbon-Atom Addition Reactions

C(S,R) + C <=> D + C(S,R3) 0.33 0.0 0.0

C(S,R3) + CH2(S) <=> CH(S,R) + CH(S) 6.0E19 0.0 0.0

CH(S,R) + H <=> CH2(S) 0.3 0.0 0.0

STICK

! Other Radical-Termination Reactions

C(S,R3) + H2 <=> CH2(S,R) 0.3 0.0 0.0

STICK

C(S,R3) + H <=> CH(S,R2) 0.3 0.0 0.0

STICK

CH(S,R2) + H <=> CH2(S,R) 0.3 0.0 0.0

STICK

CH2(S,R) + H <=> CH3(S) 0.3 0.0 0.0

STICK

CH(S,R2) + H2 <=> CH3(S) 0.3 0.0 0.0

STICK

! Graphite Reactions

CH3 + C(R,G) <=> G + CH3(S) 3.0E-2 0.0 0.0

STICK

C + C(R,G) <=> G + C(S,R3) 3.0E-2 0.0 0.0

STICK

C2H2 + C(R,G) <=> G + HCCH(S,R) 3.0E-2 0.0 0.0

STICK

C(R,G) + H <=> CH(S,G) 3.0E-2 0.0 0.0

STICK

CH(S,G) + H <=> C(R,G) + H2 2.14E-2 0.0 7300.0

STICK

CH(S,G) + G + H <=> CH(S,R) + CH(S) 2.14E-1 0.0 7300.0

STICK

END

Figure 8.5. An example of the SURFACE CHEMKIN input file to the Surface Linking File (the surface reactions are taken from Reference 8.13). The symbols R, S, D and G means radical, surface species, diamond and graphite respectively. The numbers which follow the symbol R are the number of unpaired electrons on the surface radical species.

8.4 Application codes

Having executed all the various computer packages and created the relevant linking files, the subroutines are now ready to be called upon by the application codes to simulate the CVD growth process. In the present study two such application codes were used namely the SENKIN and the SPIN application codes.

(a) SENKIN

SENKIN^8.14 is a Fortran computer program that computes the time evolution of a homogeneous reacting gas mixture in a closed system. The program considers five different problem types:

(a) an adiabatic system with constant pressure,

(b) an adiabatic system with constant volume,

(d) a system where the pressure and temperature are constant, and

(e) a system where the pressure is constant and the temperature is a specified function of

time.

In the case of diamond CVD process, the system employed is that where the pressure and temperature are held constant, i.e. case (d). The role of SENKIN in the modelling of experimental results obtained by MBMS will be discussed in detail in Section 8.6.

To solve a problem using SENKIN the user must access the CHEMKIN thermodynamic data base, execute the CHEMKIN Interpreter, and link the SENKIN with the CHEMKIN subroutine libraries, pass input data to SENKIN, and store the output data that is produced. Figure 8.6 shows the relationship between these various components.

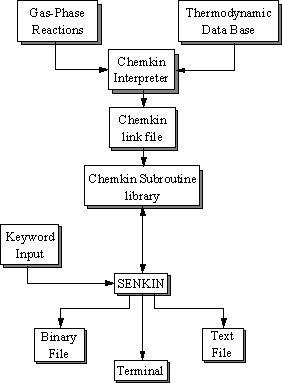
Figure 8.6. Relationship of the SENKIN program to the CHEMKIN pre-processor and the associated input and output files (Adapted from Reference 8.13)

The first step is to execute the CHEMKIN interpreter, which reads the user supplied information about the species and chemical reactions for a particular reaction mechanism. It then extracts information from the Thermodynamic Data Base about the species thermodynamic properties. A CHEMKIN link file is then written upon execution of the interpreter which in turn is accessed by the SENKIN program.

The input that defines a particular problem and the parameters required to solve it are read by the program SENKIN. The input data is read using a Keyword format that is entered in the senk.inp file (See Figure 8.7 below).

! SENK.INP

! ----------------------------------------Problem Selection

CONT

! ----------------------------------------Initial Conditions

PRES 0.026

TEMP 2000

REAC H2 0.99

REAC CH4 0.01

! ----------------------------------------Integration Control

TIME 5.0

DELT 2.0E-02

ATOL 1.0E-09

RTOL 1E-05

END

Figure 8.7. An example of the input data that is read using a Keyword format by SENKIN.

The keyword CONT will produce a solution with the temperature and pressure held constant at the initial values, and the equations solved will be those of case (d). In the above example (Figure 8.7), the initial conditions are those of an isothermal gas mixture of 1% methane (REAC CH₄) in hydrogen (REAC H₂) at 20 Torr - the units used in the input file is in atmospheres (PRES 0.026) and Kelvin (TEMP 2000). This gas mixture is allowed to react for 5 seconds (TIME 5.0), meaning that the time integration will proceed from time zero until this final time. A more detailed description of the keywords used in SENKIN can be found in Reference 8.14.

The output from program SENKIN is written in two forms: text and binary. Text output is written to display the outcome of the execution on a terminal, while the binary file restores a copy of the run. The information written to both text outputs include a summary of the initial conditions and printouts of the partial solution at a selected time interval. The full solution is written in the binary file which is useful in providing initial data for restart calculations. From this output the species concentrations may be obtained, by executing a program called DATAC.EXE which converts mass fractions written in the SENKIN output file into species mole fractions. The final result is therefore species mole fractions as a function of reaction time. An example of this is shown in Section 8.5.

(b) SPIN

SPIN^8.15 is one of the application codes supplied with the CHEMKIN software package which construct and solve a system of differential equations describing a physical problem (in the case of SPIN, a CVD reactor), using standard subroutines from various modules which together form the complete simulation package. Thus SPIN simulates the flow of chemically reacting fluid towards a growth surface on which gas-phase species can react. The gas-phase chemistry is modelled by a set of chemical reactions with rate constants provided by the gas-phase CHEMKIN module. The transport properties of the gas-phase species are continually evaluated by the TRANSPORT fitting module. Finally the production/consumption of gas-phase species on the growth surface is accounted for by a set of surface chemical reactions with rate constants calculated by the SURFACE CHEMKIN module (See Figure 8.4). Figure 8.8 shows an example of a typical SPIN input file.

! SPIN.INP Figure 8.8. Input file of the SPIN application code.

! Input file for SPIN application code. Full details of the different keywords used is found

! in Reference 8.15.

!---------------Problem type

COMP

!NOFT

STAG

!TGIV

ENRG

!RSTR

!---------------Solution Method Options

!USTG

!---------------Newton iteration controls.

ATOL 1.E-8

RTOL 1.E-3

NJAC 20

!---------------Time step controls.

ATIM 1.E-8

RTIM 1.E-3

TIME 100 1.E-6

TIM2 100 1.E-6

UFAC 2.0

DFAC 2.2

DTMN 1.E-10

DTMX 1.E-4

TJAC 20

ISTP 100

IRET 10

!---------------Solution bound controls.

SFLR -1.0E-04

SPOS 1.E-13

!---------------Grid control parameters.

NPTS 20

NMAX 65

!JJRG 90

!PCAD 0.75

!RGTC 1.0

GRAD 0.9

CURV 0.9

GRID 0.00

GRID 0.02

GRID 0.04

GRID 0.06

GRID 0.08

GRID 0.10

GRID 0.12

GRID 0.14

GRID 0.16

GRID 0.18

GRID 0.20

GRID 0.22

GRID 0.24

GRID 0.26

GRID 0.28

GRID 0.30

GRID 0.32

GRID 0.34

GRID 0.36

GRID 0.38

GRID 0.40

!---------------Initial guess & reactor operating

! conditions.

PRES 0.026

TINF 2173

TDSK 1173

!RADB

AINL 0.0

OINL 0.0

UINF 1.0

XSTR 0.0

XCEN 0.2

XEND 0.4

WMIX 0.2

TEMP 0.0 2173

TEMP 0.4 1173

!----------------Set gas concentration at in-let

REAC H₂ 0.9429

REAC H 0.0471

REAC CH₄ 0.01

!----------------Set initial guess of gas concentrations at disk

PROD H₂ 0.990041

PROD H 0.723930E-06

PROD CH₄ 0.991787E-02

PROD CH₃ 0.162266E-06

PROD CH₂ 0.902875E-13

PROD CH 0.317941E-18

PROD C 0.135916E-20

PROD C₂H₆ 0.656252E-07

PROD C₂H₅ 0.246341E-10

PROD C₂H₄ 0.119802E-04

PROD C₂H₃ 0.522252E-10

PROD C₂H₂ 0.285896E-04

PROD C₂H 0.109323E-14

!----------------Set initial guess of surface concentrations

!SURF CH(S) 9.51E-01

!SURF C(S,R) 4.87E-02

!SURF HCCH(S,R) 6.11E-15

!SURF CH2(S) 3.98E-04

!SURF CH(S,R) 2.23E-05

!SURF C(R,G) 1.00E-04

!SURF CH(S,G) 1.00E-04

!SURF H2CCH(S) 1.16E-14

!SURF CH3(S) 1.63E-06

!SURF CH2(S,R) 1.00E-07

!SURF CH2*(S) 1.64E-04

!SURF C(S,R3) 1.05E-08

!SURF CH(S,R2) 1.00E-07

!----------------Set activity of bulk phases

!ACT D 0.9999

!ACT G 1.0E-04

!---------------Multicomponent transport options.

MULT

!TDIF

!TRCE

!REOR

!GFAC 1E-04

!SFAC 1E-04

!---------------Chemistry control options.

!---------------Printing options.

PRNT 2

!---------------Miscellaneous.

END

A full description of the keywords used in the SPIN input file is shown in Reference 8.15. From the SPIN output the species concentrations may be obtained, by executing a program called SPDAT.EXE which converts mass fractions written in SPIN output file into species mole fractions. The final result is species mole fractions as a function of distance from (in this case) the filament to the substrate surface. An example of this is shown in Section 8.5.

8.5 Numerical simulation of the diamond CVD process

The first time that we attempted to run the SPIN simulation code, it crashed reporting that the matrix, which is constructed to solve the differential equations governing the mathematical problem, was singular. A considerable amount of time was spent breaking the problem into a number of simpler problems which could be analysed in greater detail in order to find the origin of the singularity.

In order to test the formulation of the gas-phase part of the problem in isolation, a simpler problem was examined involving only the gas-phase reactions, using the SENKIN application code. This code considers an isothermal gas mixture maintained at constant pressure and temperature (Section 8.4 (a) ) and calculates how the composition of the mixture changes as a function of time as a result of the chemical reactions. The results that were obtained for a mixture of 0.3% CH₄ in H₂ held at 2000K (Figure 8.9) were very similar to results reported by Harris et al.^8.2 This confirmed that the gas-phase CHEMKIN module was working correctly.

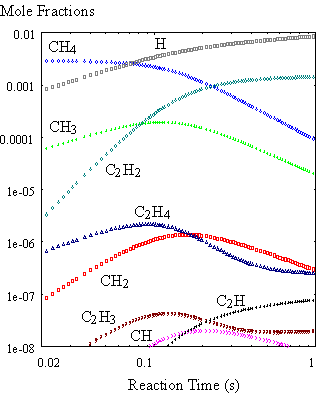
Figure 8.9. Calculated time history of gas composition. The calculation is carried out using the SENKIN code for isothermal conditions at 2000K for an initial source gas mixture of 0.3% CH₄ in H₂ (99.7%).

It was later discovered that the SPIN application code could be run with empty surface reaction files (non existent surface reaction files cause it to crash), without it running into singularity problems. In this way, the flow of a chemically reacting fluid towards a chemically inert surface could be simulated, making it possible to check that the fluid flow was being modelled correctly, using the transport properties provided by the TRANSPORT fitting module and based on the description of the gas-phase chemistry provided by the gas-phase CHEMKIN module, but ignoring the surface chemistry. Such simulations may be compared to the results obtained by the MBMS system, in which there is currently no growth surface in the vicinity of the sampling cone. The results obtained for this simulation (Figure 8.10) showed similar trends to those reported by Dandy et al.^8.5

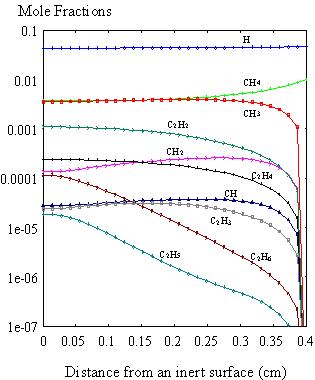
Figure 8.10. Mole fraction profiles calculated for 1% CH₄ in H₂ at 20 Torr using the SPIN application code, in the absence of surface reactions. Initial deposition conditions are: filament temperature 2000K, filament/substrate distance 4 mm (or 0.4 cm). In the above illustration, the surface is at 0 cm, and the filament is at 0.4 cm.

The next step was performed solely by Jonathan Cole^8.16, who used the SURFTHERM programming module to examine in detail the thermodynamic and kinetic data which must be provided for all surface species and surface reactions. Some of this data must be input in a special format and SURFTHERM can be used to produce tables of values over various temperature ranges: errors are revealed by the appearance of physically unreasonable values. In order to confirm that the SURFACE CHEMKIN module was working correctly, Cole used another application code called SKSAMPLE. SKSAMPLE models an idealised system consisting of a completely uniform and isothermal gas mixture lying above a chemically reactive surface. As there are no temperature or concentration gradients in the system, there is no fluid flow and the transport properties may be ignored. The net production and consumption rates of the various gas-phase and surface species are calculated from the kinetic data supplied by the gas-phase CHEMKIN and SURFACE CHEMKIN modules and SKSAMPLE predicts how the gas-phase composition and surface site fraction change with time, starting from a specified gas-phase condition. Again, SKSAMPLE could be executed successfully and gave physically plausible results.

Having ascertained that the various parts of the complete problem were correctly formulated, it appears that the mathematical singularities may have arisen because the initial guess was very far from the final solution, making the system ‘ill-conditioned’. Eventually, a search strategy was identified for conditioning the initial guess in such a way as to bring it within the domain of convergence of the computation. The initial guess may be conditioned by forcing the SPIN code to perform a ‘time evolution’, whereby the original system of equations is augmented by a time-dependent term to yield a time-dependent system, which mathematically is much less susceptible to divergence problems. The time-dependent solution is then integrated to give a much better guess to the solution of the steady-state problem. Computationally, this is more expensive and time-consuming than solving the steady-state problem from the start, but it is more reliable. A similar strategy is followed automatically by SPIN when less severe divergence problems are encountered, but the singularities found in the present simulation prevented it from even ‘getting off the ground’.

In this way the full problem, including surface reactions, was solved and the results of the simulation of a hot filament CVD reactor are shown in Figure 8.11. These also show similar trends to those reported by Dandy et al.^8.5

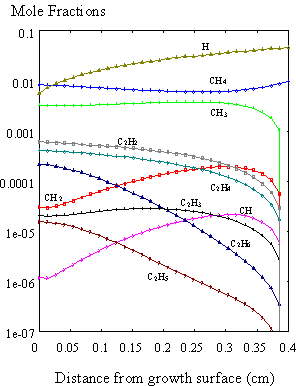
Figure 8.11. A full simulation of the diamond CVD growth process using SPIN. The species mole fractions are presented with surface reactions included in the calculations.

8.6 Numerical simulation of the gas-phase composition vs. filament temperature for 1% CH₄ in H₂ at 20 Torr

As previously mentioned in Section 8.5, It is possible to run the SPIN application code with empty surface reaction files, because such simulations may be compared to the results obtained by the MBMS system. This application code was therefore used in order to test the validity of the MBMS data. 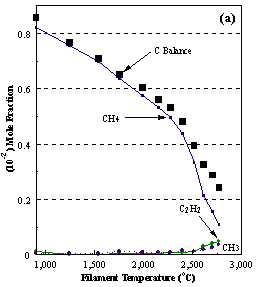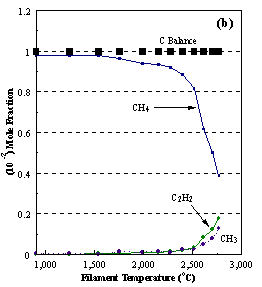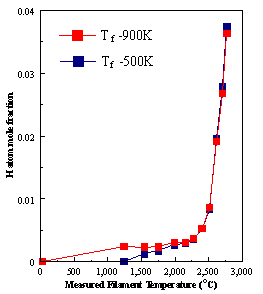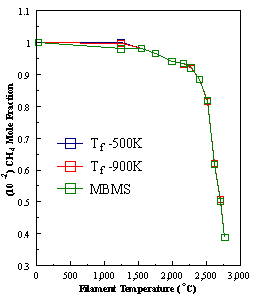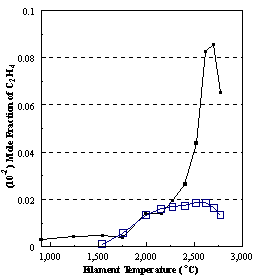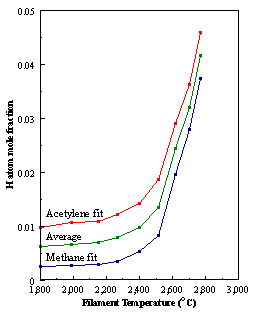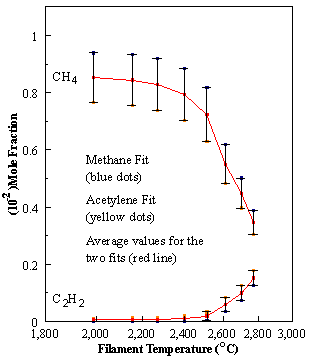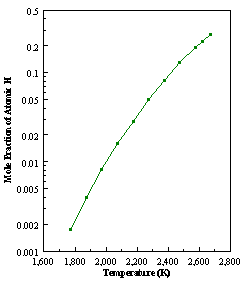Unlike the work performed by the various groups using the CHEMKIN package,^{8.2-8.7,8.9,8.13} for the first time a numerical simulation of the gas-phase composition using a 1% CH₄ in H₂ gas mixture as a function of filament temperature was performed, in precisely the same way in which the MBMS result are presented. 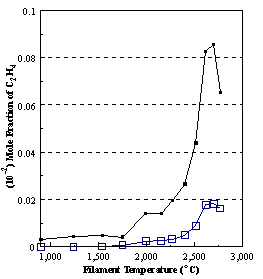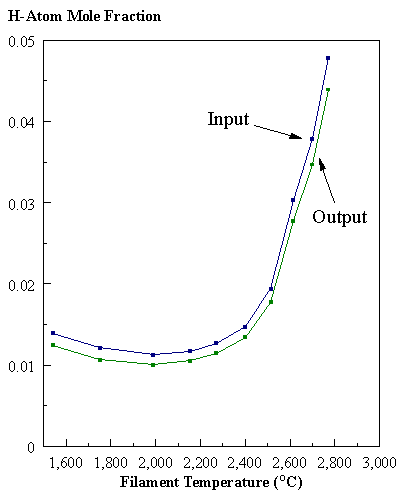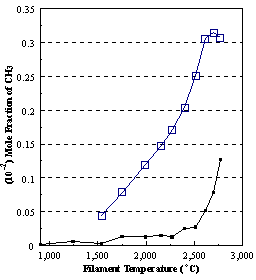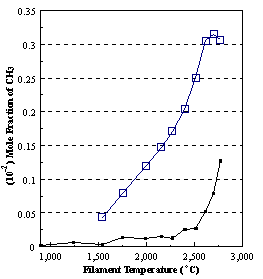Figure 8.12 shows how the distribution of the major observable stable gas-phase species [CH₄ (m/e = 16), C₂H₂ (m/e = 26)] and methyl radicals (m/e = 15), measured by MBMS, vary as a function of filament temperature for an initial feedstock of 1% CH₄ in H₂ measured 4 mm from the filament. 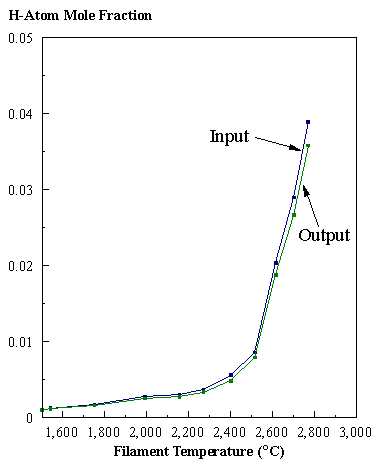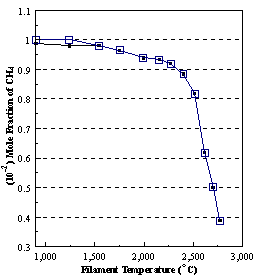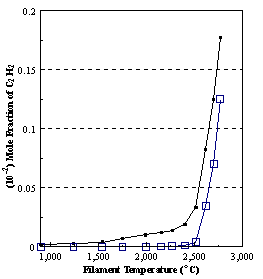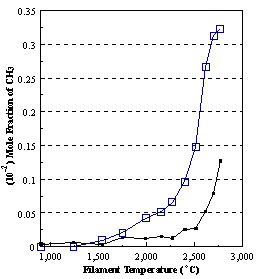The data is presented in two forms: (a) with no thermal diffusion corrections being made, and (b) with thermal diffusion corrections being made in the calculations. Note that the carbon balance, defined as (total C fraction measured)/(C fraction in the feed gas) and shown as a black filled square in Figure 8.12 (b), is constant (and equal to one) throughout. In the present work, the SPIN application code was performed without including the thermal diffusion keyword in the input file, and so we are simulating the variation in the concentrations of the hydrocarbon species as a function of filament temperature shown Figure 8.12 (b).

Figure 8.14. Initial H atom input concentration required by SPIN to simulate the CH₄ mole fraction. Two sets of input temperatures were used: T_g = T_f-500K and T_g = T_f-900K where T_g and T_f are gas temperature and experimentally measured filament temperature respectively.

Filament Temperature (T_f) measured during MBMS measurements (°C)	Filament Temperature (T_f) (K)	Gas Temperature (T_g) used in SPIN input file (K)	Substrate Temperature (T_s) used in the SPIN input file (K)
23	296	296	296
1240	1513	1013	664
1540	1813	1313	796
1750	2023	1523	888
1990	2263	1763	993
2155	2428	1928	1065
2270	2543	2043	1116
2400	2673	2173	1173
2515	2788	2288	1223
2615	2888	2388	1267
2700	2973	2473	1305
2770	3043	2543	1335

Table 8.1. Gas temperatures (T_g) and substrate temperatures (T_s) used for the SPIN input file to simulate gas-phase composition vs. filament temperature for 1% CH₄ in H₂ at 20 Torr. The gas temperature is taken to be 500K less than the measured filament temperature. The values for the substrate temperatures were obtained assuming that the ratio between the filament : substrate temperature observed at growth conditions (2400°C : 900°C) is true for all the filament temperatures measured.

Filament Temperature (T_f) measured during MBMS measurements (°C)	Filament Temperature (T_f) (K)	Gas Temperature (T_g) used in the SPIN input file (K)	Substrate Temperature (T_s) used in the SPIN input file (K)
23	296	296	296
1240	1513	613	664
1540	1813	913	796
1750	2023	1123	888
1990	2263	1363	993
2155	2428	1528	1065
2270	2543	1643	1116
2400	2673	1773	1173
2515	2788	1888	1223
2615	2888	1988	1267
2700	2973	2073	1305
2770	3043	2143	1335

Table 8.2. Gas temperatures (T_g) and substrate temperatures (T_s) entered in the SPIN input file to simulate gas-phase composition vs. filament temperature for 1% CH₄ in H₂ at 20 Torr. The gas temperature is taken as 900K less than the measured filament temperature.

The values for T_g = T_f-500K were chosen as input for all subsequent SPIN simulations because a decrease in temperature of similar magnitude was observed with distance from the filament (between 0 and 1 mm away from the filament).^8.2,8.17

Table 8.3 below shows the H atom concentration require to simulate the CH₄ mole fraction. Inspection of this table reveals that the values for [H] calculated by SPIN (output file) are very close to those of the values used in the input file. This means that the initial guesses for the [H] are reasonable estimates for the actual amount present in the CVD reactor at any given temperature. This is illustrated graphically in Figure 8.15.

Gas Temperature (T_g) (K)	[H] input (CH₄ fit)	[H] output (CH₄ fit)	[H] (average) (CH₄ fit)
296	0	0	0
1013	5 × 10^-6	4.9 × 10^-6	0.000005
1313	0.00125	0.00117602	0.001213
1523	0.00175	0.00161946	0.001685
1763	0.00275	0.00252492	0.002637
1928	0.00300	0.00276149	0.002881
2043	0.00366	0.00337292	0.003516
2173	0.00560	0.00488882	0.005244
2288	0.00860	0.00793842	0.008269
2388	0.02040	0.01878490	0.019592
2473	0.02898	0.02664350	0.027829
2543	0.038945	0.03581780	0.037384

Table 8.3. [H] required to simulate the variation in the mole fraction of methane as a function of filament temperature measured 4 mm from the filament for 1% CH₄ in H₂ at 20 Torr. The output data from SPIN and the calculated species mole fractions are given in six significant figures.

Figure 8.15. Schematic showing the H atom concentration calculated by SPIN after the simulation vs. the input values used (to simulate the CH₄ mole fractions).

Figure 8.16 shows how the other hydrocarbon species measured using MBMS compared with the SPIN simulation. Note that this particular simulation was intended to match the CH₄ mole fractions.

Figure 8.18. Comparison between the mole fractions of the major hydrocarbon species (CH₄, CH₃, C₂H₂, and C₂H₄) calculated by SPIN (open squares) and those measured by the MBMS system (filled squares).

Again the mole fractions of the other hydrocarbon species calculated are accurate to within a factor of between 1-4, and in reasonable agreement with those measured by the MBMS system. When simulating the C₂H₂ mole fraction, the inability to measure accurately low concentrations of C₂H₂ using the MBMS system at low temperatures means that an unfeasibly high [H] input had to be implemented in the SPIN input file, and so the low MBMS temperature readings have been ignored. The two experimentally measured hydrocarbon species that closely match the SPIN calculations are CH₄ and C₂H₂. As Figure 8.19 shows the H atom mole fractions required by SPIN to simulate the CH₄ data was slightly different than those required to simulate the C₂H₂ data. An average value for the [H] was calculated for the two separate simulations, and so average values for the [CH₄] and [C₂H₂] were obtained as a function of filament temperature, and shown in Figure 8.20 (red line). The error bars represents the discrepancy in mole fraction of one specie when fitting the data for the other specie.

Figure 8.19. H atom mole fraction required by SPIN to simulate the variation of [CH₄] (blue line) and [C₂H₂] (red line) as a function of filament temperature. The green line represents the average values for the two fits.

Figure 8.20. SPIN simulation of 1% CH₄ in H₂ vs. filament temperature. The blue dots represents the values of mole fractions obtained when performing the methane fit. The yellow dots represents the values of mole fractions obtained when performing the acetylene fit. The red line represents the average values for the two simulations. Error bars are shown to illustrate the discrepancies in the mole fractions inherent in one specie (CH₄ or C₂H₂) when performing a simulation for the other specie (C₂H₂ or CH₄).

8.7 Filament poisoning effects

One of the main problems with hot filament CVD is the gas temperature drop, or discontinuity, that occurs at the filament. Some research groups have found using thermocouples that the gas temperature in the vicinity of the filament can be up to 1000K below the filament temperature.^8.2,8.17 The extent of this temperature discontinuity seem to be dependent on the amount of energy provided to the filament. A possible explanation for this is the role played by the filament in H₂ decomposition. There is considerable evidence to show that the molecular hydrogen dissociates into atomic hydrogen primarily through catalytic reaction on the filament surface.^8.18,8.19 The rational for this comes from the observations that measured H concentrations decrease dramatically upon increasing CH₄ in the feed gas.^8.18,8.19 The process whereby a hydrocarbon or hydrocarbon radical fragment reduces the effective concentration of H atoms produced at the filament is known as the filament poisoning effect. This effect need to be taken into account when choosing an appropriate starting [H]. Hsu^8.18 carried out a series of experiments in which the filament temperature was held constant at 2620K, and the inlet CH₄ concentration was varied between 0.4% and 7.2%. Hsu found that as the amount of CH₄ in the system was increased, less power was required to maintain the filament at 2620K. The reason for this is that more reactive sites on the filament become obstructed by increasing CH₄, thus reducing the power supplied to the filament to initiate the H₂ decomposition, resulting in higher filament temperature.

The main assumption built into the numerical simulation is the inlet H:H₂ ratio (See Tables 8.5 and 8.6 for a list of [H]/[H₂] values used in this study to simulate the MBMS results).

Gas Temperature (T_g) (K)	[H]/[H₂] input (%) (CH₄ fit)	[H]/[H₂] output (%) (CH₄ fit)	[H]/[H₂] (average) (%) (CH₄ fit)
296	0.000	0.000	0.000
1013	0.001	0.000	0.000
1313	0.126	0.1189	0.123
1523	0.177	0.1638	0.170
1763	0.279	0.2557	0.267
1928	0.304	0.2797	0.292
2043	0.371	0.3418	0.356
2173	0.569	0.4962	0.533
2288	0.876	0.8082	0.842
2388	2.104	1.933	2.019
2473	3.015	2.764	2.891
2543	4.095	3.749	3.922

Table 8.5. [H]/[H₂] ratios used in order to simulate the variation in the mole fraction of CH₄ as a function of filament temperature for 1% CH₄ in H₂ at 20 Torr.

Figure 8.21. Numerical simulation of a hot filament system containing only H₂.

Gas Temperature (T_g) (K)	[H]/[H₂] input (%) (C₂H₂ fit)	[H]/[H₂] output (%) (C₂H₂ fit)	[H]/[H₂] (average) (%) (C₂H₂ fit)
296	-	-	-
1013	-	-	-
1313	1.426	1.272	1.349
1523	1.241	1.090	1.166
1763	1.154	1.024	1.089
1928	1.196	1.034	1.115
2043	1.297	1.175	1.236
2173	1.511	1.378	1.445
2288	1.999	1.828	1.913
2388	3.159	2.886	3.022
2473	3.975	3.628	3.802
2543	5.078	4.636	4.857

Table 8.6. [H]/[H₂] ratios used in order to simulate the variation in the mole fraction of C₂H₂ as a function of filament temperature for 1% CH₄ in H₂ at 20 Torr.

In the absence of methane (and surface reactions which also reduces the effective concentration of H₂ at the substrate c.f. Figures 8.10 and 8.11) the variation of the atomic H concentration as a function of filament temperature is shown above in Figure 8.21, consistent with the simulation performed by Dandy and Coltrin.^8.5 In their study however, instead of studying the dependence of species distributions on filament temperature (which is the subject of the present work), they varied the inlet methane concentration between 0.4% and 7.2%, whilst holding the filament temperature, T_f, fixed at 2620K. To simulate the effects of filament poisoning without attempting to model the heterogeneous chemistry occurring there, they proposed a simple ‘poisoning formula’,

where X_H is the H atom mole fraction at the filament, and 0.004 £ X_CH4 £ 0.072.

The term R is the mole fraction ratio of X_H2 / X_H. At 2620K, they predicted a value of R of 3.46 at X_CH4 = 0, which they viewed as the minimum value that R will attain in the system. It is then assumed that R varies linearly with X_CH4, reaching a maximum value R_max when X_CH4 = 0.072. In order to use this functional form for R(X_CH4), the slope of the line or another value of R must be known. On a trial and error basis, by attempting to minimise the differences between the numerical and experimental results, they found that good agreement at X_CH4 = 0.072 was obtained using R_max » 100. As it turns out this estimate agreed very closely to the results observed in this present simulation studies. Assuming that this linear dependence of R with X_CH4 is true, the slope of this line is therefore:

The equation of the line is therefore

(8.2)

In the present study, X_CH4 = 0.01 (1%), therefore,

R(X_CH4 = 0.01) = 1340.8 × 0.01 + 3.46 = 16.87

so the H atom mole fraction at 2620K where X_CH4 = 0.01 becomes,

A good estimate for the inlet [H] for SPIN would therefore be 0.0554. Subsequent simulation using this value for H showed very good agreement with measured species concentrations by the MBMS system.

Since the present work is more involved with studying the dependence of species distributions as a function of filament temperature, ideally we would like to obtain a range of values of R (and hence X_H) vs. filament temperature, for a given input CH₄ concentration. Since Dandy and Coltrin performed experiments based on a fixed temperature regime, an additional assumption has to be made in order to make any progress in the present endeavour. At a filament temperature of 2620K, the ratio of X_H (X_CH4 = 0.01): X_H (X_CH4 = 0) is 0.0554/0.22576 = 0.246. Assuming that this ratio is independent of filament temperature, then the degree of H atom loss due to filament poisoning is such that only ~25% of X_H predicted by the SENKIN code is actually present at the filament. Figure 8.22 shows how the concentration of atomic H varies as a function of temperature:(a) using pure hydrogen in the system, (b) when 1% CH₄ is present in the gas mixture and (c) calculated by SPIN in order to model the MBMS results. At high gas temperatures (³ 2250K), there is a remarkable correlation between the simulated results (b) and (c), which suggests that the assumption made above accurately predicts the true H atom concentration in the CVD reactor at growth conditions. At lower temperatures, deviation from the fit between (b) and (c) becomes more prominent with decreasing temperature. This may again be due to our inability to obtain accurate values of detected species at low concentrations, which precludes the possibility of obtaining sensible numerical simulations by SPIN.

Figure 8.22. Variation of [H] vs. temperature: (a) using pure H₂ in the system; (b) calculated when 1% CH₄ is present in the gas mixture, based on the assumptions outlined in the text; (c) required by SPIN to model the MBMS measurements.

8.8 References

8.1 R.J. Kee, F.M. Rupley and J.A. Miller, Sandia National Laboratories Report SAND89-8009B, 1989.

8.2 S.J. Harris, A.M. Weiner and T.A. Perry, Appl. Phys. Lett., 53 1605 (1988).

8.3 D.G. Goodwin and G.G. Gavillet, J. Appl. Phys., 68 6393 (1990).

8.4 E. Meeks, R.J. Kee, D. S. Dandy and M.E. Coltrin, Combustion and Flame 92 144 (1993).

8.5 D.S. Dandy and M.E. Coltrin, J. Appl. Phys., 76 3102 (1994).

8.6 D.G. Goodwin, Appl. Phys. Lett., 59 277 (1991).

8.7 T. Lang, J. Laimer and H. Störi, Diamond. Relat. Mater., 3 470 (1994).

8.8 R.J. Kee, F.M. Rupley and J.A. Miller, Sandia National Laboratories Report SAND87-8215B, 1993.

8.9 S.J. Harris J. Appl. Phys., 65 3045 (1989).

8.10 E. Meeks, R.J. Kee, D.S. Dandy and M.E. Coltrin, Combustion and Flame 92 144 (1993).

8.11 K.Y. Lee, M.H. Yang and I.K. Puri, Combustion and Flame 92 419 (1993).

8.12 M.E. Coltrin, R.J. Kee and F.M. Rupley, Sandia National Laboratories Report SAND90-8003C, 1991.

8.13 M.E. Coltrin and D.S. Dandy J. Appl. Phys., 74 5803 (1993).

8.14 A.E. Lutz, R.J. Kee and J.A. Miller, Sandia National Laboratories Report SAND87-8248, 1994.

8.15 M.E. Coltrin, R.J. Kee, G.H. Evans, E. Meeks, F.M. Rupley and J.F. Grcar, Sandia National Laboratories Report SAND91-8003, 1993.

8.16 Jonathan Cole, private communication.

8.17 G. Leyendecker, J. Doppelbauer, D. Bauerle, P. Geittner and H. Lydtin, Appl. Phys. A., 30 237 (1983).

8.18 W.L. Hsu, Appl. Phys. Lett., 59 1427 (1991).

8.19 F.G. Celii and J.E. Butler, Appl. Phys. Lett., 54 1031 (1989).

Gas Temperature (T_g) (K)	[H] input (C₂H₂ fit)	[H] output (C₂H₂ fit)	[H] (average) (C₂H₂ fit)
296	-	-	-
1013	-	-	-
1313	0.013920	0.0124402	0.0131801
1523	0.012135	0.0106763	0.0114057
1763	0.011290	0.0100416	0.0106658
1928	0.011700	0.0105321	0.0111161
2043	0.012680	0.0114993	0.0120897
2173	0.014740	0.0134579	0.0140990
2288	0.019400	0.0177758	0.0185879
2388	0.030319	0.0277884	0.0290537
2473	0.037851	0.0346969	0.0362740
2543	0.047840	0.0439242	0.0458821