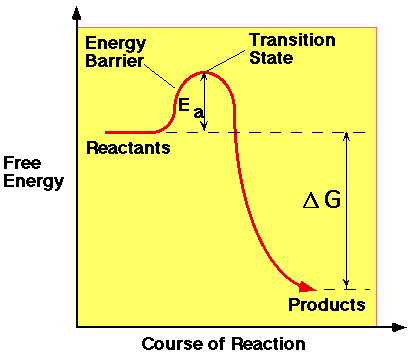
When an exothermic reaction occurs, the free energy of the reactants is higher than the free energy of the products. However, energy is often needed to start the reaction. This supply of energy is known as the Activation Energy (E_a). It is the energy needed to break bonds in the reactants and to allow the less stable intermediates, or transition state, of the reaction to form. Only when this barrier has been breached, can the reaction proceed via the downhill pathway, which can be seen on the diagram below.

In an explosive reaction, ignition involves giving the explosive material the activation energy to start deflagaration. Energy can be given in various forms depending on which type of stimulus is used. Friction, impact and heat initiation may provide thermal, potential or kinetic energy to the system while electrical impulses would supply electrical energy. Once the reaction has started, deflagaration can then provide heat energy to the system to allow the rest of the explosive to react.

Deflagaration involves generation of gases and heat, which leads to an increase in pressure. How and why does this occur? The Ideal Gas Law can help to explain this.

The Law describes how an ideal gas behaves with reference to the volume, the pressure and the temperature of the surroundings, as well as the amount of gas present. The gases we see around us are not actually ideal gases due to attractions and repulsions between gas molecules but the Law gives a good approximation of how they behave.

During an explosion in a confined space, the volume (V) remains constant. R is known as the gas constant and so also remains constant. This allows the equation above to be modified to give:

Here k is just a number. This means that pressure (p) has a directly proportional relationship with temperature (T) and the number of moles (n) in the mixture, as the number of moles will always increase due to many smaller molecules being made from one big one.

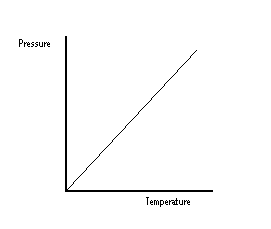
From this graph, it can be seen that if temperature is increased, pressure is increased. As a lot of heat is generated in deflagaration, and the volume remains the same, the pressure in the container becomes greater and greater until the walls can no longer remain intact.

On the molecular scale, the reason is simple. Pressure is a measure of how often molecules hit the walls or sides of an object. As temperature is increased, the molecules are given more energy and they can therefore move faster. The faster they travel, the more often they will hit the walls of a bomb casing, and so the pressure increases. The molecules are also able to hit the walls with a greater force. Once the force and number of hits is great enough, the casing can no longer resist and detonation occurs to cause an explosion.

Back / Home / Next