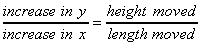
4 Basic differentiation

Differentiation is all about calculating the slope or gradient of a curve y(x), at a given point, x.

The gradient is the

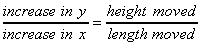
Notation: We use the symbol , Δ delta, to mean a (large) change in the value of a variable. If, say, x changes from a value of x₁, to a new value, x₂, then

So the gradient of a curve y(x) can be written as:

gradient =

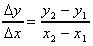
Linear Equations

For a straight line graph of equation y(x) = mx + c, the gradient is given simply by the value of m.

Examples

• y = 3x + 6, gradient = 3

• y = 5x - 3, gradient = 5

• y = -2x + 1, gradient = -2

• y = 6 - 3x, gradient = -3

Measuring gradients

If we don't know the equation of the straight line, we can work out the gradient by tabulating the values of y vs. x and plotting the graph.

Example Values of y and x are given below, what is the gradient?

x	-3	-2	-1	0	1	2	3
y	-11	-8	-5	-2	1	4	7

Graphical Method

(i) Plot graph

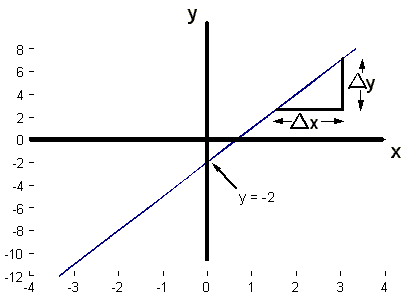
(ii) Choose any 2 points along the line (x₁,y₁) and (x₂,y₂)

(iii) Draw the triangles (as in the diagram), or just calculate x and y.

(iv) Calculate gradient from: gradient =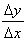

Numerical Method: choose the points we have values for, say, (-2, -8) and (1,1). We now have:

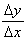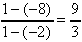gradient = = = 3

Since the intercept is at y = -2, we know that the eqn. of this line must be

Finding the gradient of a general function

Linear curves are simple, but how do we find the slope of any curve, y(x) at the point x ?

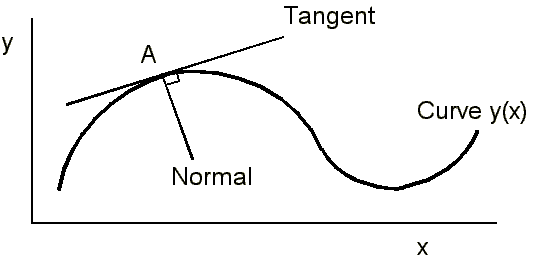
The gradient of the curve at point A is the same as that of the tangent at point A. So, all we need to do is construct the tangent and measure its gradient, Δy / Δx.

Example What is the gradient of y(x) = x² - 4x - 1 when x = 4?

Solution Plot out the curve, then construct the tangent when x = 4 by eye, as best you can. Measure the gradient Δy / Δx by completing the triangle.

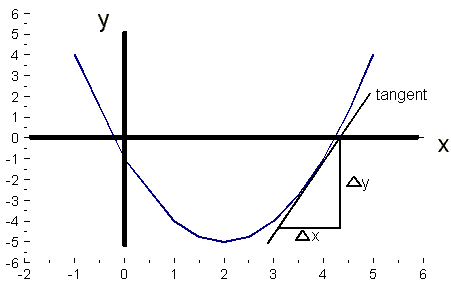
Graphically, we find that 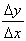= 4.

Analytical Differentiation

Drawing tangents is a rather cumbersome method of obtaining gradients. Is there an analytic method?

The answer is differentiation. A simplified derivation of this is given in the handout, but we only really need to learn the 'magic formula' (see below).

Notation: The slope, or gradient, or differential, or derivative can be written in many equivalent ways:

y = = =

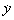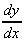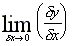
For other variable names and functions, there is the equivalent notation.

e.g. for s(t), we have ,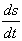

for E(ν), we have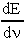

for φ(λ), we have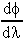

Differentiation 'magic formula' (for standard polynomials)

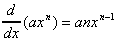
To differentiate a polynomial function, multiply together the leading factor, a, and the exponent (power),. n, then subtract one from the exponent.

Examples

1. y = x² , = 2x

2. y = 2x³, 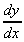= 6x

3. y = 9x²⁷, 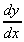= 243x²⁶

4. u = 3m⁶, 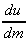= 18m⁵

5. φ = 7λ, 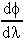= 7

6. Ψ= ,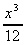

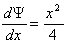
7. p = -5q², 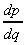= -10q

8. y = 5, 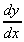= 0       The differential of a constant is always zero, i.e. its slope is zero, as we'd expect.