
7. Trigonometrical Functions
The common trig. functions are defined relative to a right-angled
triangle.

In calculus, we need the angles measured in radians rather than degrees, with
so that 1 radian = 360° / 2π.
The common points used:
For graphs of the common trig functions, see handout 2.
Inverse Trig. Functions
If y = sin x, then x = sin-1y (also called arcsin y)
y = cos x, then x = cos-1y (also called arccos y)
y = tan x, then x = tan-1y
(also called arctan y).
Examples
1. sin x = 0.32, x = sin-10.32 = 18.7 = 0.33 rads
2. tan x = 0.87, x = tan-10.87 = 41 = 0.71 rads
Differentials of Trig functions
It can be shown that if
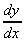 = cos x
= cos x
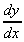 = - sin x
= - sin x
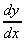 =
= 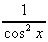
We often meet compound functions in many applications and we can
use the Product, Chain and Sequential rules as before.
Examples
1. y = sin(kx)
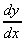 = cos(kx).k = kcos
(kx) important
= cos(kx).k = kcos
(kx) important
2. y = 3cos x - 4sin(x2)
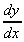 = -3sin x - 4 cos(x2).2x
= -3sin x - 4 cos(x2).2x
= -3sin x - 8x.cos(x2)
3. y = 7sin(5x2) + 6ln {tan(5x)}
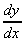 = 7cos(5x2).10x
+
= 7cos(5x2).10x
+ 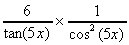 5
5
= 70x.cos(5x2) + 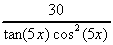
4. Ψ(x) = Asin 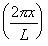 , a typical
wave function for an electron in an orbital.
, a typical
wave function for an electron in an orbital.
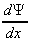 = Acos.
= Acos.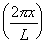
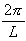
= 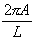 .cos
.cos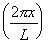 .
.
8. Integration - Calculating Areas
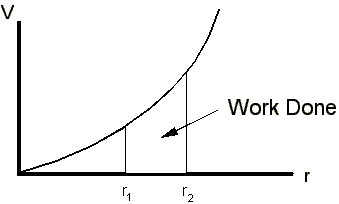
In science, we often need to work out the area under a
graph. For example the work done to move a charged particle a
distance r through a potential difference V is given by
the area under the potential vs distance curve.
Another example is the total distance travelled by an object moving at velocity v(t), (which is a function of time so that the object is accelerating), is given by the area under the v(t) vs t graph.
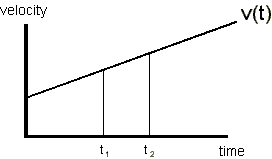
Calculating Areas - counting squares
The most obvious way to calculate the area under a graph is to
draw it on graph paper and count the squares.
Example What is the area under the curve y(x)
= 2x2 from x = 1 to x
= 3?
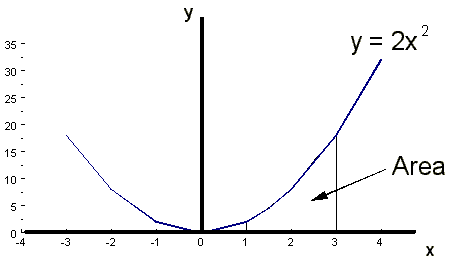
a) Divide the area up into 2 trapezia
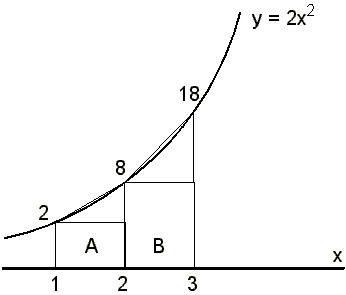
Area of trapezium = Area of rectangle + area of triangle
= (length x width) + (½ x length x height)
Area of A = (1 x 2) + (½ x 1 x 6) = 5 units
Area of B = (1 x 8) + (½ x 1 x 10) = 13 units
Total Area = A+B = 5+13 = 18 sq. units
b) Now do it again with 4 trapezia
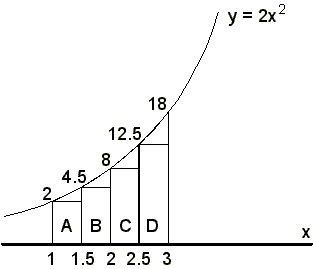
Area of A = (½ x 2) + (½ x ½ x 2½) = 15/8
Area of B = (½ x 4½) + (½ x ½ x 3½) = 33/8
Area of C = (½ x 8) + (½ x ½ x 4½) = 51/8
Area of D = (½ x 12½) + (½ x ½ x 5½) = 75/8
Total Area = A+B+C+D = 17.75
sq.units
You can see that as we divide up the area into smaller and smaller
strips, the approximation to the area gets better and better.
This is the basis for numerical solutions of areas (e.g.
Simpson's Rule - see textbooks).
The actual value of the area will be achieved when we have an
infinite number of strips, of width zero!
Needless to say we do not have to do this - there's a short cut
- analytic integration
Integration - Notation
The area under a curve, y(x), which has been divided
up into many strips of width x between the limits of x
= a and x = b is given by adding up all the
areas of the strips ( width x height).
width x height).
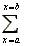 (height of strip) x
(width of strip)
(height of strip) x
(width of strip)
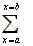 y(x). δx
y(x). δxNow, as x approaches 0 (i.e. the strips get vanishingly thin) we can replace the Σ with an integration sign which is an extended S, for sum.
So we get:
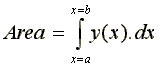
The dx now serves to tell us what the name of the variable
is - we say 'with respect to x'
This process is called integration
Integration as the Reverse of Differentiation
We know that the differential of y(x) = x3 is 3x2. The process of reversing this, whereby we generate a function from its derivative is integration.
i.e. 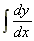 = y(x), so that integration
of a differential gives the original function.
= y(x), so that integration
of a differential gives the original function.
and 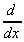 [
[![]() y(x).dx]
= y(x), so that differential of an integral gives the original function.
y(x).dx]
= y(x), so that differential of an integral gives the original function.
Compare other reversible functions such as:
 Next lecture
Next lecture