1S Summer Exam 2003 - Calculus Dr Paul May

1. Answer all parts (a) to (d).

Determine the following:

(a) dy/dx     if       y = 5x⁹          (1 mark)

(b) dk/dp      if       k = 3p⁶ + 17p - 6          (1 mark)

(c) dβ/dθ      if       β = -5cos θ           (2 marks)

(d) dj/dm      if       j = 73e^-25m          (2 marks)

2. Answer all parts (a) to (d). All parts carry equal marks.

Differentiate the following functions with respect to x, and simplify the result where possible:

(a) y = (3x + 2)(1 - 11x)           (b) y = -55x¹² ln x

(c)                      (d) y = tan (x⁶ - 3x²)           (8 marks)

3. Answer all parts (a) to (c).

Consider the function:     y(x) = 5 sin(2x + π/2),     where x is in radians.

(a) Differentiate this function, and thence determine the co-ordinates (x,y) of the stationary points and whether they are local maxima or minima.          (5 marks)

(b) Hence sketch this function between x = 0 and x = π.         (3 marks)

(c) Calculate the area under this function between x = 0 and x = π/4.
      [Hint: the relationship     sin(-m + π/2) = cos m      might be useful].          (2 marks)

Answers

1) [1 mark for (a) and (b), 2 marks for the rest].

a) dy/dx = 45x⁸              b) dk/dp = 18p⁵ + 17

c) dβ/dθ = +5sin θ          d) dj/dm = -1825e^-25m

2) [2 marks each].

a) Product Rule:     (3x + 2).(-11) + (1 - 11x).3    =    -19 - 66x

b) Product Rule:     -55x¹²(1/x) + (ln x).(-660 x¹¹)     =    -55x¹¹ (1 + 12 ln x)

c) Quotient Rule:           =     

d) Funct. of a Funct.:      [1 / {cos² (x⁶ - 3x²)}] . (6x⁵ - 6x)     =     

3) If you look at the function, you can see that it is just a sine wave with 5 times the normal amplitude, twice the normal frequency, and a phase offset of π/2 (90°).

a) Using Func. Of Func. Rule,     dy/dx = 5cos(2x + π/2) .2      =    10cos(2x + π/2)

At the t.p., dy/dx = 0,    so 10cos(2x + π/2) = 0,     so cos(2x + π/2) = 0.

Since cos^-1(0) = π/2, 3π/2, 5π/2,... etc, then:

(2x + π/2) = π/2, 3π/2, 5π/2, etc.




When (2x + π/2) = π/2, 2x = 0, so x = 0, and y = 5, which gives a t.p at (0, 5)

or when (2x + π/2) = 3π/2, 2x = π, so x = π/2, and y = -5, which gives a t.p at (π/2, -5)

and when (2x + π/2) = 5π/2, 2x = 2π, so x = π, and y = -5, which gives a t.p at (π, 5) ...etc.

b) d²y/dx² = -20sin(2x + π/2),      
and at x = 0 this has a value of -20. So this t.p. is a maximum.

At x = π/2, d²y/dx² has a value of +20, so it's a minimum.

At x = 3π/2, d²y/dx² has a value of -20, so it's a maximum.

So it's an oscillating function (as you might expect for a sine wave), with repeating maxima and minima.

c) The sine function will take values from +1 to -1, so y will oscillate from +5 to -5. The x multiplier is 2, so the function will oscillate with twice the frequency of a normal sine wave, i.e. one wavelength every π rather than every 2π.



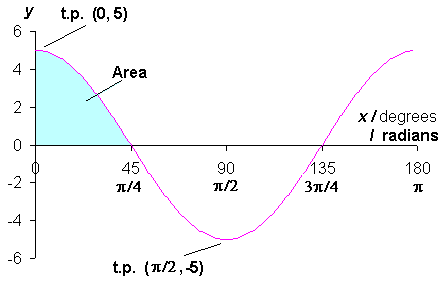
d) We cannot integrate the original function easily, but using the relationship:

sin(-m + π/2) = cos m

we can see that 5sin(2x + π/2) = 5cos (-2x), which is much easier to integrate:

Area =       =      

      =     5/2 - 0     =      2.5 sq. units