1S Summer exam 2009 - Calculus Dr Paul May

 

1.      Answer all parts (a) to (d). All parts carry equal marks.

 

Determine the following:

 

            (a) dy/dx   if    y = 5x26

 

(b) du/dh if    u = 2.3h3 + (3Χ10‑6)h

 

(c) dΩ/dy   if    Ω = 7 tan y

(d) d―/dO   if    ― = 2 exp(–4O) ‑ 3O
                                                                                                            (4 marks)

 

2.      Answer all parts (a) to (d).  All parts carry equal marks.

Differentiate the following functions with respect to x, and simplify the result where appropriate:

 

(a)                                          (b) y = 6e-3x cos x

 

(c)                                             (d) y =  3 ln
                                                            (8 marks)

 

3.      Answer all parts (a) to (c).

 

      Consider the function:          y = (x – 1)3 (5x ‑ 1)

 

(a) Differentiate this equation and hence find the co-ordinates of the stationary point(s).

                                                                                                                        (4 marks)

 

(b) Find the second differential of this equation, and hence find whether the stationary point(s) is/are a local maximum, minima or points of inflection.

                                                                                                                        (4 marks)

 

(c) Sketch the function between x = 0 and x = +3.

                                                                                                            (4 marks)

Answers

 

1)

a) dy/dx = 130x25                                   b) du/dh = 6.9h2 + 3Χ10-6

c) dΩ/dy = 7 / cos2y                             d) d―/dO = ‑8 exp(‑4O) ‑ 3

 

2)

 

a) Rules for Indices:      y = ½x‑3 – 3x-5/4 +                    dy/dx = ‑(3/2)x-4 ‑ (15/4)x-9/4

                                                                                             = 

 

b) Product Rule:           6e-3x ( -sin x)  +  (cos x) (-18e-3x)         =   ‑6e–3x (3cos x + sin x)

 

c) Quotient Rule:           =

 

 

d) Funct. of a Funct.:    dy/dx =  3 Χ (5 / x3) Χ 3x2/5   =  9 / x

 

 

3)  (a)   y = (x – 1)3 (5x ‑ 1) =

 

Most students multiplied out the brackets and then differentiated it, but this is a bad idea since the multiplication is tricky and takes many lines, so many students made mistakes in this.  But also the function you get is a quartic polynomial, which is easy to differentiate but which is almost impossible to factorise to find the turning points. 

 

  Use Product Rule, plus F-of-F Rule and it only takes 2 lines:

             = (x – 1)3 (5)  +  (5x ‑ 1)Χ3(x – 1)2Χ (1)

 

             = 5(x – 1)3  + 3(x – 1)2(5x – 1)

 

At t.p. =0,   so   5(x – 1)3  + 3(x – 1)2(5x – 1)= 0,

 

So, factorising:   (x ‑ 1)2 { 5(x – 1) + 3(5x – 1) }  = 0

 

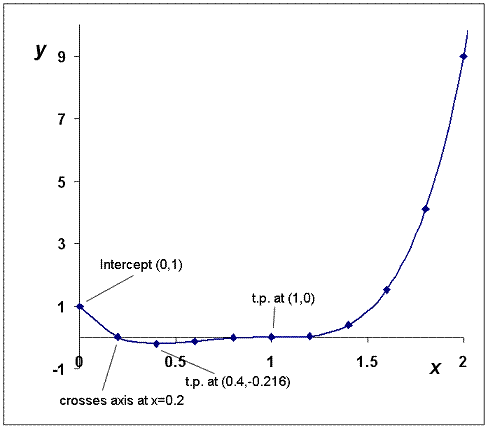
So either      (x – 1)2 = 0,   which means x = 1 and therefore y = 0,

 

Or     5(x – 1) + 3(5x – 1)  =  5x – 5 + 15x – 3 = 0,  which means  x = 8/20   (0.4) and y = ‑0.216.

 

So there are only 2 t.p.s, at    (1, 0)  and   (0.4, ‑0.216)

 

[For a quartic function you’d expect 3 t.p.s, so if we only got two either we did it wrong or this is a clue that one of the t.p.s might be ‘special’]

 

  (b) d2y/dx2 = 15(x – 1)2  + 3(x – 1)2(5) + (5x – 1) Χ 6(x – 1) 

 

                        = 30(x – 1)2  + 6(5x – 1)(x – 1) 

 

  (i) When x = 1, d2y/dx2 = 0, so this is a point of inflection. 

  (ii) When x = 0.4, d2y/dx2 = 7.2, i.e. +ve, so it’s a minimum.

 

 (c) Need to sketch graph, get correct shape, label axes properly, and label the turning points and places where it crosses the axes to get full marks.

 

From original eqn:

When x = 0, y = +1.

When x = 1, y = 0  (the p.o.i)

When x = large and +ve, y = tends to 5x4, i.e. also large and positive