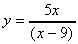d) y = sin (x2
+ 3) (7 marks)
1) Determine the following:
a) dy/dx if y = x2 b) dy/dr if y = 3r6 - r + 1
c) dy/dx if y = 3cos x d) dp/dq
if p = 5e-q (7 marks)
2) Differentiate the following functions with respect to x,
and simplify the result where possible:
a) y = (x + 1)(x - 1) b) y = x ln x
c) 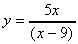d) y = sin (x2
+ 3) (7 marks)
3) A function which is often used to represent the form of an electronic wavefunction in certain atoms is:
a) This function has 3 stationary points. One is at r
= 0, and another at r = infinity. Differentiate this function
and thence determine the coordinates (y,r) of the
remaining stationary point. (6 marks)
b) The second differential of this function is:
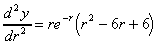
Determine whether the stationary point you just found is a local
maximum or minimum. (2 Marks)
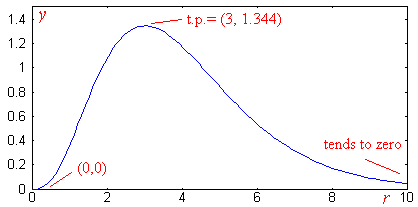
c) Hence sketch this function between r = 0 and r =
infinity. (3 marks)
1) [1mark for (a), 2 marks for the rest].
a) dy/dx = 2x b) dy/dr = 18r5 - 1
c) dy/dx = -3sin x d) dp/dq
= -5e-q
2) [1 mark for (a), 2 marks for the rest].
a) Product Rule: (x + 1).1 + (x-1).1 = 2x
b) Product Rule: x(1/x) + (ln x).1 = 1 + ln x
c) Quotient Rule: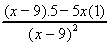 
= 
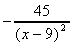
d) Function of a Function: cos (x2 + 3).2x
= 2x cos (x2 + 3)
3) a) [6 marks in total]
Product Rule: -r3e-r + e-r(3r2) = r2e-r(3 - r)
For turning point, r2e-r(3
- r) = 0, so either:
r2 = 0, so that r = 0,
e-r = 0, so that r = infinity
or (3 - r) = 0, so that r = 3
The last answer is the required one. So the turning point is at (3, 1.344).
b) Determine the sign of the second differential, d2y/dr2.
Putting in the value of r = 3, we get d2y/dr2
= -0.448, which is -ve, so the t.p. is a local maximum.
[2 marks]
c) Sketch: 3 marks
