Nanoparticles are larger than individual atoms and molecules but are smaller than bulk solid. Hence they obey neither absolute quantum chemistry nor laws of classical physics and have properties that differ markedly from those expected.

There are two major phenomenons that are responsible for these differences.

First is the high dispersity of nanocrystalline systems. As the size of a crystal is reduced, the number of atoms at the surface of the crystal compared to the number of atoms in the crystal itself, increases. For example, a 4 nm diameter CdS nanoparticle has about 1500 atoms, of which about a third are on the surface. Properties, which are usually determined by the molecular structure of the bulk lattice, now become increasingly dominated by the defect structure of the surface.

 

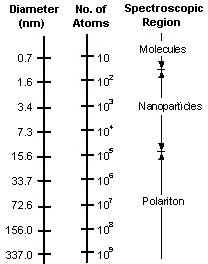
The diagram above shows a schematic representation of the different sizes.

The second phenomenon occurs noticeably only in metals and semiconductors. It is called size quantisation and arises because the size of a nanoparticle is comparable to the de Broglie wavelength of its charge carriers (i.e. electrons and holes). Due to the spatial confinement of the charge carriers, the edge of the valance and conduction bands split into discrete, quantized, electronic levels. These electronic levels are similar to those in atoms and molecules.

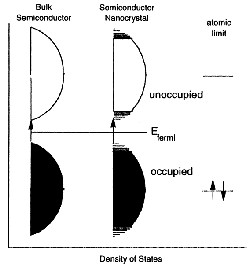
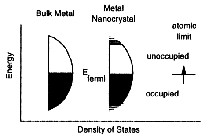
In diagrams the conduction and valence bands in  the  solid,  nanoparticle and atom state of a  semiconductor (left) and a metal (above) are compared. It can be seen here again that nanoparticles represent a state of matter in the transition state between bulk solids and individual atoms.

The spacing of the electronic levels and the bandgap increases with decreasing particle size. This is because the electron hole pairs are now much closer together and the Coulombic interaction between them can no longer be neglected giving an overall higher kinetic energy.

This increase in bandgap can be observed experimentally by the blue-shift in the absorption spectrum or sometimes even visually by the colour of the samples. A larger bandgap means that more energy is required to excite an electron from the valance band to the conduction band and hence light of a higher frequency and lower wavelength would be absorbed.

By changing the particle size of the same material,  and hence the energy bandgap, different coloured samples can be obtained.

The increase in molar absorption coefficient shows that the oscillator strength also increases as particle size decreases. This is due to the strong overlapping of the wave functions of confined charge carriers. Experiments carried out in the past have found the absorption spectrum to be potential dependent, with decreasing wavelengths as applied potential decreases. This change is fully reversible before the threshold potential.