|
Density Functional Theory
|
Kohn
and Hohenberg showed, in 1964, that all the properties of a molecular
system can be determined from the electron density
function, ρ, of the system.[27]
The energy of a system is a function of the density function, often called
a functional:
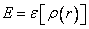 |
(9.1) |
This means the ground state Hamiltonian can be derived from the density
function. Coupled with the Kohn-Hohenberg variational
theorem, it is possible to determine the energies and densities
of a molecular system, by virtue of the fact that the true ground state
electron density minimises the energy functional, just as the true ground
state wavefunction minimises the Schrödinger energy.
Density functional theory (DFT) also accounts
for electron correlation effects. This, and the fact that it is computationally
only marginally more time consuming than a good Hartree-Fock calculation
(which does not include electron correlation effects), has led to widespread
use of DFT. However, DFT is not strictly an ab initio method,
as it does not directly solve the Schrödinger equation. It is included
because of its popularity, and it is certainly a valid method, but some
people are reluctant to regard it as an ab initio method. The
fact that it uses an approximate functional means that DFT can sometimes
yield energy values below the true ground state energy. It is also only
accurate for ground state symmetries, although work has been done on extending
its use for excited states.
Kohn was awarded half of the Nobel
Prize for Chemistry in 1998 for his work on density functional theory.
An in-depth discussion of density functional theory is also given in Levine.[7]
|
| «
Previous | Next » |
[27]
P. Hohenberg and W. Kohn, Phys. Rev., 136,
B864, 1964 |