There are a number of ways of calculating Pi.
The first is a method which has been in use since the ratio was first discovered, and this is simply of measuring the circumference and diameter of a large circle, and dividing one by the other. This is a fairly rudimentary method, and the larger the circle the smaller the error. It can never be very good though.

The first person to geometrically calculate Pi, (despite the absence of basic algebra and trigonometry, which hadn't been invented), was Archimedes.
Archimedes stated that if you inscribe a regular polygon, and you also ascribe a regular polygon, both with 3*2n-1 then you can define an increasing sequence, b1, b2, b3.. and another a1, a2, a3.. both with limits of Pi. Using trig we can define each of these terms as;
an = K tan(p/K), bn = K sin(p/K),
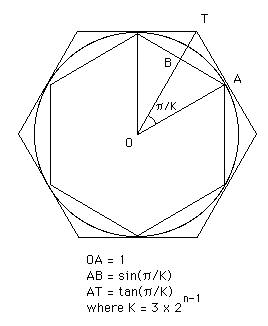
Archimedes calculated the a6 and b6 terms by purely geometrical means, and showed that b6 < p < a6. Using polygons of up to 96 sides he defined Pi as 3.1418. Other people used this technique to find very large numbers of decimal places. (See the history of Pi section).
The next method of calculation was invented in the renaissance, and this was the arithmetic progression. The best known was invented by James Gregory and this is:
p/4 = 1 - 1/3 + 1/5 - 1/7 + ....
This is not a lot of use as it takes 10000 terms to find 4 correct decimal places.
A better progression, and in fact the one still used today in many computer algorithms is:
![]()
This is a refinement of Gregory's formula and was developed by Machin in 1706.
There is another way to calculate Pi, but it is a very rudimentary method. It was devised by Georges Buffon, and is called the needle method. If you have a grid of parallel lines, each a distance 1 apart, and a needle of length k<1 then you can use the method. If you drop the needle randomly on the grid then the probability of the needle falling across a line is defined by 2k/p. The more throws you do the better the approximation will, be although it will always be a very rough method. (See the blunders and hoaxes section, also the crazy stuff section).
You can try computer simulation of this method which is fun if you like that kind of thing at:
http://www.angelfire.com/wa/hurben/buff.html
Tenuous link: American Pie
Picture taken from http://www.geocities.com/Hollywood/Studio/9480/americanpie2.htm